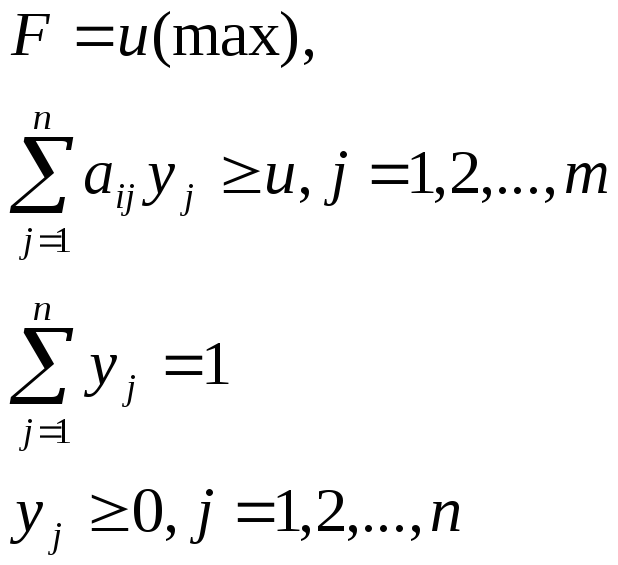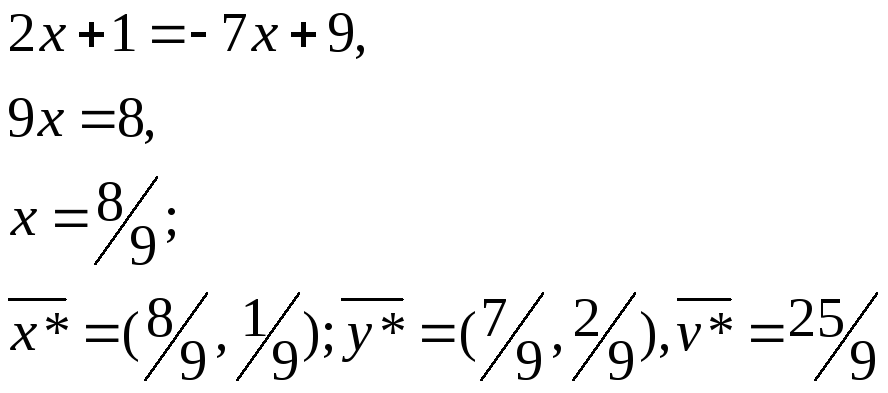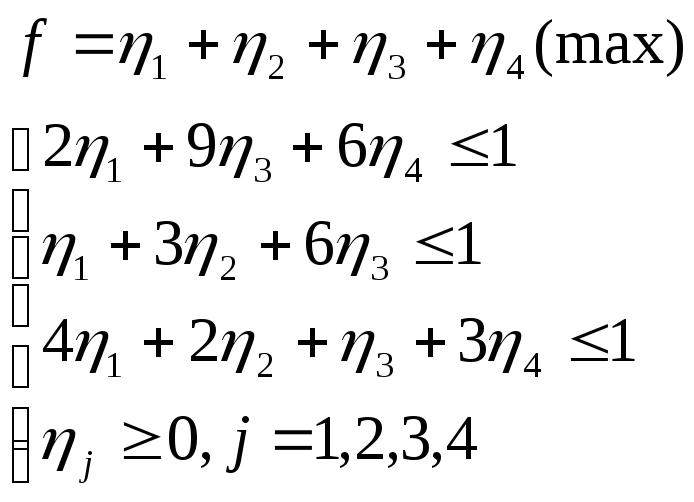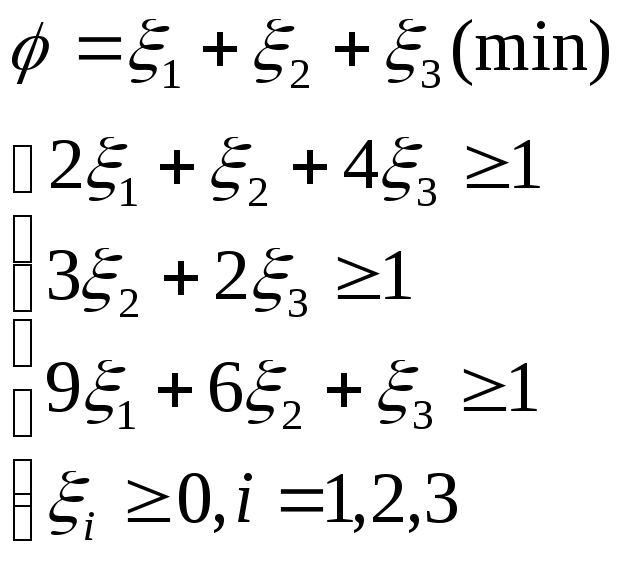Методичка по лабораторной работе №5 [новая]

Лабораторная работа № 4

Решение матричных игр

Цель работы

Ознакомиться с методами решения задач матричных игр методами линейного программирования [1,2].

Методические указания

Постановка общей задачи теории игр

Теория игр – математическая теория конфликтных си­туаций. Экономические соревнования, спортивные встречи, боевые операции – примеры конфликтных ситуаций. Про­стейшие модели конфликтных ситуаций – это салонные и спортивные игры.

В игре могут сталкиваться интересы двух противни­ков (игра парная или игра двух лиц), интересы n (n > 2) противников (игра множественная или игра n лиц). Су­ществуют игры с бесконечным множеством игроков.

Стратегией игрока называется система правил, одно­значно определяющих выбор поведения игрока на каждом ходе в зависимости от ситуации, сложившейся в процессе игры. В зависимости от числа возможных стратегий игры делятся на конечные и бесконечные.

Процесс игры состоит в выборе каждым игроком i одной своей стратегии.В результате сложившейся ситуации s игрок i получает выигрыш.

Игры, в которых целью каждого участника является получение по возможности большего индивидуального выигрыша, называются бескоалиционными в отличие от коалиционных, в которых действия игроков направлены на максимизацию выигрышей коллективов (коалиции) без дальнейшего разделения выигрыша между участниками.

По определению бескоалиционной игрой называется система

,

в которой I и – множества, – функции на множестве принимающие вещественные значения.

Бескоалиционная игра называется игрой с постоянной суммой, если существует такое постоянное C, что для всех ситуаций .

Ситуация s в игре называется приемлемой для игрока i, если этот игрок, изменяя в ситуации s свою стратегию s_i на какую-либо другую s_i', не может увеличить своего выигрыша.

Ситуация s, приемлемая для всех игроков, называется ситуацией равновесия.

Процесс нахождения ситуации равновесия в бескоали­ционной игре есть процесс решения игры.

Матричные игры

Игра называется парной, если в ней сталкиваются интересы двух противников. Игра называется с нулевой суммой, если один игрок выигрывает столько, сколько второй проигрывает в той же партии.

Каждая фиксированная стратегия, которую может вы­брать игрок, называется его чистой стратегией.

Матричной называют парную игру с нулевой суммой при условии, что каждый игрок имеет конечное число чистых стратегий.

Пусть первый игрок имеет m чистых стратегий, а вто­рой – n.

Парная игра с нулевой суммой задается ' формально системой чисел – матрицей, элементы которой определяют выигрыш первого игрока (и соответственно проигрыш второго), если первый игрок выберет i-ю строку (i-ю стратегию), а второй игрок j-й столбец (j-ю стра­тегию). Матрица называется платежной матрицей или матрицей игры.

Задача первого игрока – максимизировать свой выиг­рыш.

Задача второго игрока – максимизировать свой выиг­рыш – сводится к минимизации проигрыша второго, что эквивалентно задаче минимизации выигрыша первого игрока.

Чистые стратегии

Гарантированный выигрыш первого игрока, применяю­щего чистую i-ю стратегию,

Число называется нижним значением игры, а соответствующая чистая стратегия i₀, при которой достигается называется максиминной стратегией первого игрока. Аналогично, называется верхним значением игры а j₀ – минимаксной стратегией второго игрока.

Всегда . Если то игра имеет седловую точку в чистых стратегиях; число называется значением игры (или ценой игры). Игра имеет седловую точку в чистых стратегиях тогда и только тогда, когда существует элемент матрицы , минимальный в своей строке и в то же время максимальный в столбце

(1)

Любая пара (i₀, j₀), обладающая свойством (10.1), называется седловой точкой.

Смешанные стратегии

Если обозначить через x₁, x₂, …, x_m вероятности (частоты), с которыми первый игрок выбирает соответ­ственно первую, вторую, . . ., m-ю чистую стратегию, так что через ; через y₁, y₂, …, y_n вероятности, с которыми второй игрок выбирает первую, вторую, ,.., n-ю свою чистую стратегию, причем , то наборы чисел x=( x₁, x₂, …, x_m) и y=(y₁, y₂, …, y_n) называются смешанными стратегиями первого и второго игроков соответственно. Каждый игрок имеет бесчисленное множество смешанных стратегий. Множество смешанных стратегий первого иг­рока обозначим через s₁ и множество смешанных страте­гий второго игрока – через s₂.

Задача первого игрока состоит в выборе такой стра­теги чтобы при отсутствии информации о выборе другого максимизировать свой выигрыш. Задача второго игрока состоит в выборе такой стратегии , чтобы при отсутствии информации о поведении первого игрока минимизировать выигрыш первого.

Если первый игрок применяет стратегию, а второй – стратегию то средний выигрыш M(x, y) первого игрока равен

Выигрыш M(x, y) называют функцией игры.

Например, в задаче с матрицей

первый игрок имеет две чистые стратегии , и бесчисленное множество смешанных страте­гий, таких, как , и т. д.; все они являются элементами множества второй игрок имеет четыре чистые стратегии и бесчисленное множество смешанных стратегий, таких, как , являющихся элементами множества

Если первый игрок применяет смешанную стратегию , а второй применяет стратегию, то средний выигрыш первого игрока, опре­деляемый функцией игры, окажется равным

Если же первый игрок применяет стратегию, а второй — стратегию , то . Оптимальная стратегия первого игрока второго игрока; —цена игры.

Седловая точка в смешанных стратегиях

Пара смешанных стратегий (х*, у*) называется седловой точкой функции М(х, у), если

(2)

Каждая матричная игра с нулевой суммой имеет решение в смешанных стратегиях, т. е. существуют такие смешан­ные стратегии х* и y* первого и второго игроков соответ­ственно, что выполняется условие (10.2). Гарантирован­ный выигрыш первого игрока, применяющего смешанную стратегию

Стратегия х*, при которой гарантированный выигрыш первого игрока достигает максимального значения, назы­вается оптимальной стратегией первого игрока:

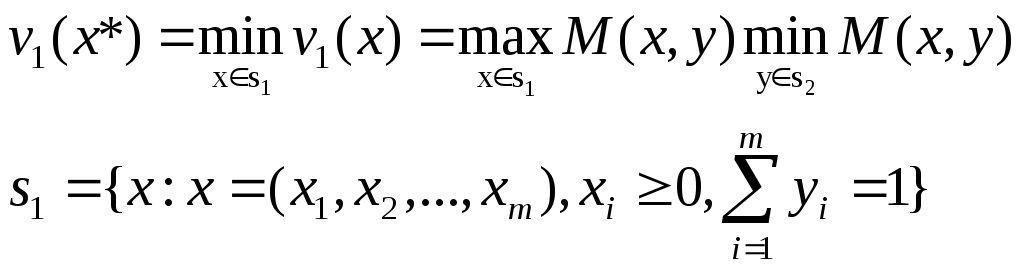
Гарантированный проигрыш второго игрока

y* – оптимальная стратегия второго игрока, если

Гарантированный выигрыш первого игрока, применяю­щего свою оптимальную стратегию, равен гарантирован­ному проигрышу второго игроку, применяющего свою оптимальную стратегию: – цена игры.

Сведение задачи теория игр к задаче линейного программирования

Задача максимизации гарантированного выигрыша пер­вого игрока и задача минимизации гарантированного проигрыша второго игрока сводятся к паре взаимно двой­ственных задач линейного программирования:

Задача первого игрока	Задача второго игрока

Процесс решения задач упрощается, если перейти к Пе­ременным . Это возможно, если.

Имеем:

Задача первого игрока	Задача второго игрока

Оптимальные стратегии игроков не изменятся, если мат­рицу игрызаменить на . Цена игры при этом увеличивается на с.

Методы решения задач теории игр

Методы решения задач теории игр во многом зависят от условий задачи и от матрицы А выигрышей первого игрока.

1) Если матрица А имеет седловую точку, то решение игры сводится к нахождению седловой точки матрицы А. Оптимальные стратегии игроков определяются при этом координатами _(i,j) седловой точки матрицы А, а цена игры элементом в седловой точке.

Пример 1. Найти оптимальные стратегии игроков и цену игры:

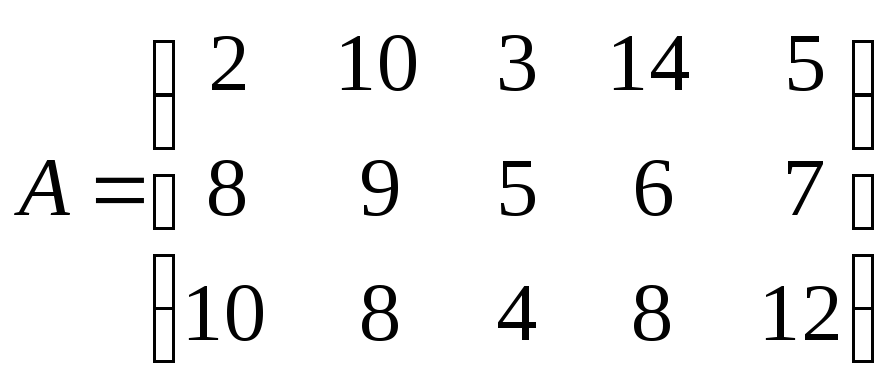
Минимизируя элементы первой строки, получим, что –

, аналогично, , .

Максимизируя элементы по столбцам, получим: _. Нижняя цена игры определяется путем максимизации :

Верхняя цена игры определяется минимизацией :

Имеем, так что . Игра, определяемая матрицей _A, имеет седловую точку (2, 3). Задача разрешима в чистых стратегиях. Оптимальный способ игры найден. Придерживаясь чистой второй стратегии, первый игрок обеспечивает себе выигрыш, не меньший 5, второй игрок, применяя чистую третью стратегию, проигрывает не более 5. Обе стратегии _i=2 и _j=3 являются оптимальными для первого и второго игроков. Цена игры v=5.

2) Если матрица А имеет размерили, то решение задачи может быть получено графически.

Иногда процесс решения задачи можно упростить, если вычеркнуть из матрицы доминируемые (неполезные) стра­тегии. Вычеркнутым стратегиям соответствуют нулевые компоненты в смешанных стратегиях. Стратегия i₀ для первого игрока является доминируемой, если существует такая стратегия i₁ для первого игрока, что

или если существуют такие числа , что

Стратегия j₀ для второго игрока является доминирующей, если существует такая стратегия j₁ второго игрока, что

или если существуют такие числа , что

Пример 2. Найти оптимальные стратегии игроков и цену игры

В чистых стратегиях решения игры нет, так как

Упростим матрицуA, заметив, что

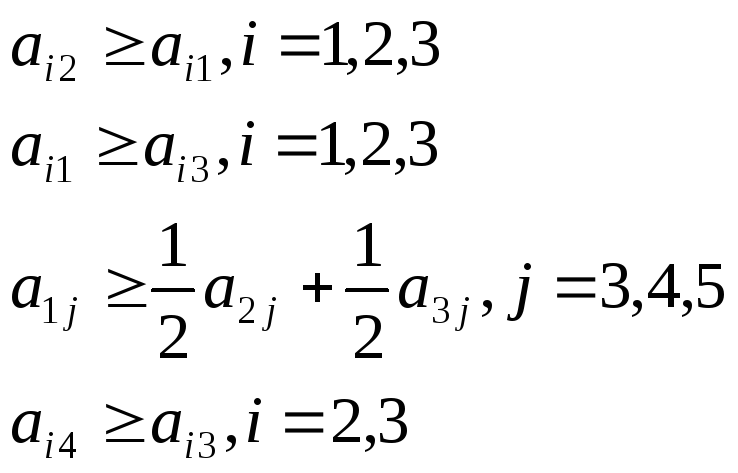
Задачу с матрицей размера 2x3 решим геометрически:

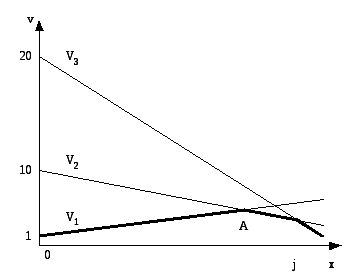
В плоскости переменных (x, v) построим – v_j(x) ожидаемый средний выигрыш первого (рис. 1) игрока, при­меняющего первую стратегию с вероятностью х при условии, что второй игрок отвечает чистой стратегией j (j=1,2,3):

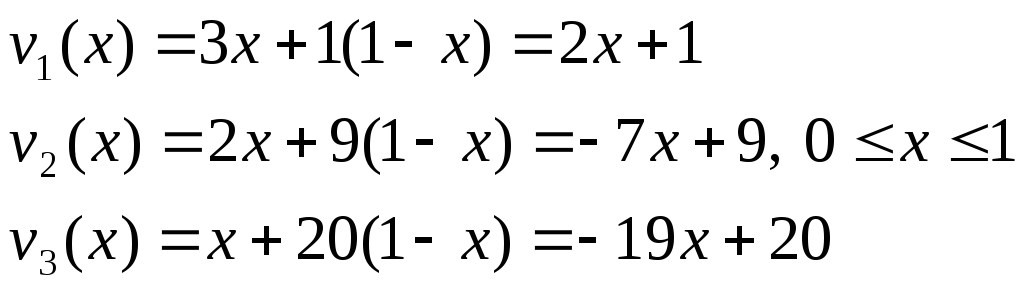
В точке А (рис. 1) пересечения прямых v1(x) и v2(x) гарантированный выигрыш первого игрока (изображенный жирной линией) достигает наибольшего значения Исходная задача с матрицей А имеет следующее решение:

3) Если задача теории игр не имеет решения в чистых стратегиях и не может быть решена графи­чески, то для получения точного решения игры ис­пользуют методы линейно­го программирования.

Целесообразно задачу второго игрока решать сим­плекс-методом. В послед­ ней симплекс-таблице, со­держащей оптимальное решение задачи второго игрока, можно найти и оптимальное решение двойственной зада­чи – задачи первого игрока.

Пример 3. Получить решение задачи теории игр, если матрица выигрышей первого игрока известна:

Очевидно, что матрица А не имеет седловой точки и что графический способ решения неприемлем.

Построим пару взаимно двойственных задач линейного программирования, эквивалентную игре с матрицей . Имеем:

Сведем задачу второго игрока к канонической задаче ми­нимизации

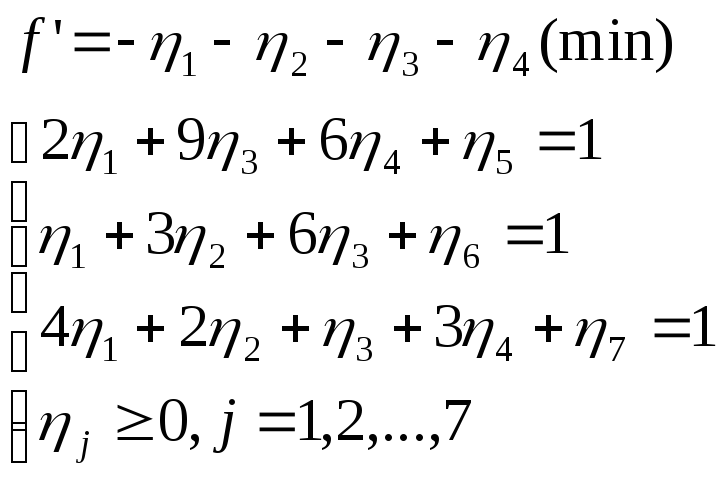
и составим симплекс-таблицу, которая приведена к базису опорного решения:

2	0	9	6	1	0	0	1		2	0	9	6	1	0	0	1
1	3	6	0	0	1	0	1		1/3	1	2	0	0	1/3	0	1/3
4	2	1	3	0	0	1	1		10/3	0	-3	3	0	-2/3	1	1/3
1	1	1	1	0	0	0	0		2/3	0	-1	1	0	-1/3	0	-1/3

Выбираем положительную оценкуи находим наименьшее отношение min{l/3, 1/2} = 1/3. С ведущим эле­ментомвыполняем жорданово преобразование таб­лицы. Получаем

-14/3	0	15	0	1	4/3	-2	1/3
1/3	1	2	0	0	1/3	0	1/3
10/3	0	-1	1	0	-2/9	1/3	1/9
-4/9	0	0	0	0	-1/9	-1/3	-4/9

Все оценки базисане положительны. Следовательно, – оптимальное опорное решение канонической задачи минимизации. По­этомуявляется оптимальным решением задачи линейного программирования и _.

Компоненты оптимального решения двойственной задачи определяются с помощью оценочной строки последней симплекс-таблицы, а именно , так что – оптимальное решение двойственной задачи. Переходя к первоначальным переменным , задачи, получим .

Наконец,

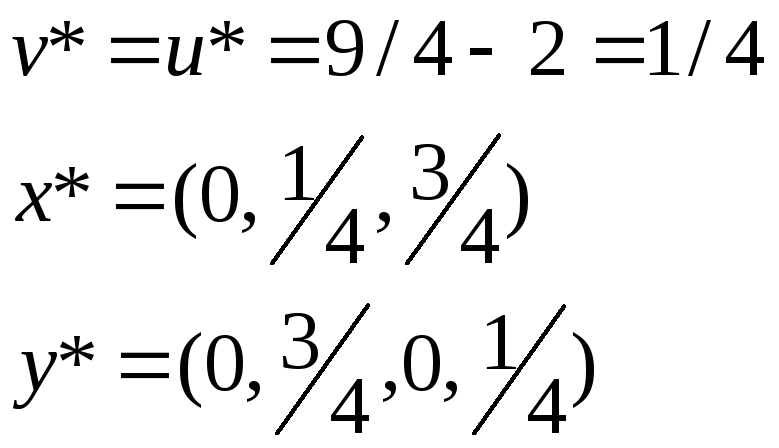
Порядок выполнения работы

1. Сделать формальную постановку задачи.

2. Определить множество возможных стратегий игроков, при этом по возможности исключить эквивалентные стратегии.

3. Выписать матрицу игры.

4. Найти оптимальные стратегии игроков, используя симплекс–метод.

Задачи для решения

1. (Морра)

Игроки одновременно показывают один или два пальца, и в тот же момент каждый из игроков называет число. Если число, названное одним из игроков, совпадает с общим числом пальцев, показываемых обоими игроками, то игрок получает со своего противника выигрыш, равный этому числу.

2. (Игра А,B,C)

Тасуется колода, состоящая из трех карт: А,B,C, и каждому из двух игроков дается по одной карте. Посмотрев свою карту, I–й игрок делает предположение относительно того, какая карта у II–го игрока.. Посмотрев на свою карту и услышав предположение I–го игрока, II–й игрок также пытается угадать карту I–го. Если какой–либо из игроков угадывает правильно, другой платит ему 1$.

3. (Упрощенный покер)

Первый игрок получает одну из карт Ст и Мл с равными вероятностями, а затем может или "сделать ставку" или "спасовать". Если первый делает ставку, то второй может "спасовать" и потерять или "уравнять игру", и выиграть или потерять в зависимости от того, имеется ли на руках у первого игрока карта Мл или Ст. Если первый игрок пасует, то второй может также пасовать, что дает выигрыш 0, или сделать ставку, выигрывая , если у первого игрока карта Мл, и теряя , если у первого игрока Ст.