Расчетно-графическая работа

Вариант 18

Задание: Задачу линейного программирования решить двумя способами:

1. симплекс методом;

2. графическим способом.

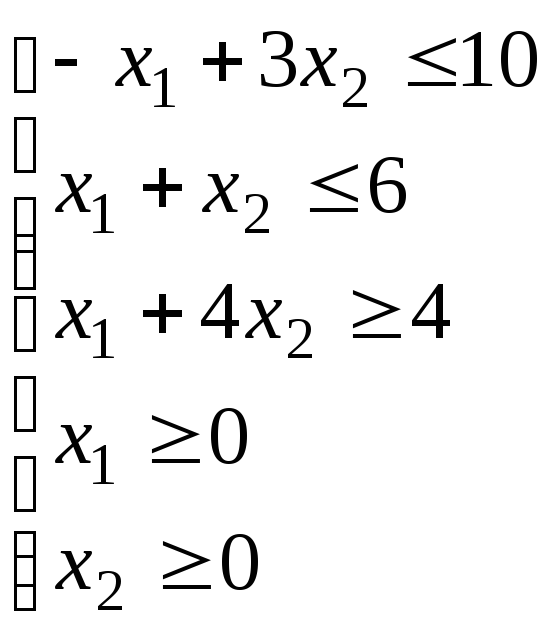
Симплекс метод

Сведем задачу к канонической путем введения дополнительных переменных

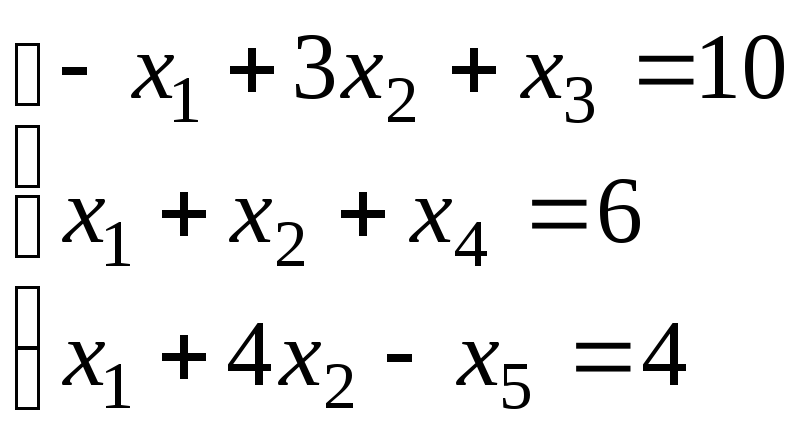
Задачу максимизации сведем к задачи минимизации путем введения новой целевой функции

х₃,х₄,х₅ – базисные переменные; х₁,х₂ – свободные переменные.

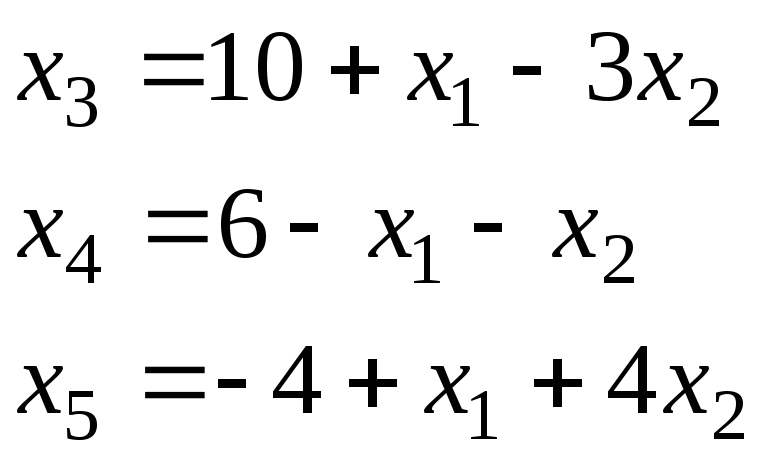
Пусть х₂=0, а переменную х₁ будем увеличивать до тех пор пока базисные переменные будут оставаться положительными. Из предыдущего выражения следует, что х₁ можно увеличивать до значения х₁=4. При больших значениях переменная х₅ станет отрицательной. Таким образом, полагая х₁=4 и х₂=0 получим новое опорное решение.

х₁⁽⁰⁾=4; х₂⁽⁰⁾=0; х₃⁽⁰⁾=14; х₄⁽⁰⁾=2; х₅⁽⁰⁾=0.

Значение целевой функции будет F⁽⁰⁾=-4.

х₁,х₃,х₄ – базисные переменные; х₂,х₅ – свободные переменные.

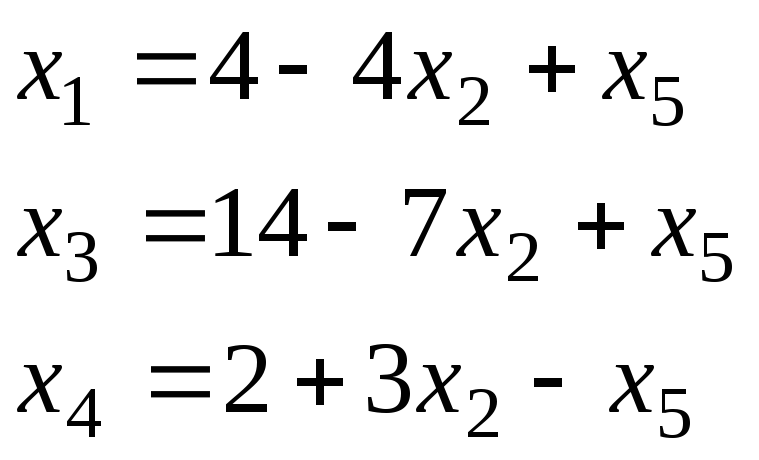
Целевую функцию запишем через свободные переменные заменив х₁.

х₂=0; х₅ увеличиваем

Получим новое опорное решение.

х₁⁽¹⁾=6; х₂⁽¹⁾=0; х₃⁽¹⁾=16; х₄⁽¹⁾=0; х₅⁽¹⁾=2.

Значение целевой функции будет F⁽¹⁾=-6.

х₁,х₃,х₅ – базисные переменные; х₂,х₄ – свободные переменные.

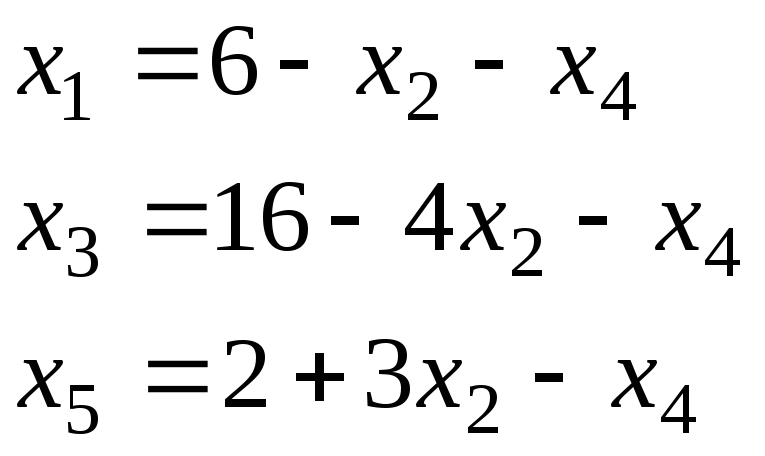
Целевую функцию запишем через свободные переменные заменив х₅.

х₄=0; х₂ увеличиваем

Получим новое опорное решение.

х₁⁽²⁾=2; х₂⁽²⁾=4; х₃⁽²⁾=0; х₄⁽²⁾=0; х₅⁽²⁾=14.

Значение целевой функции будет F⁽²⁾=-10.

х₁,х₂,х₅ – базисные переменные; х₃,х₄ – свободные переменные.

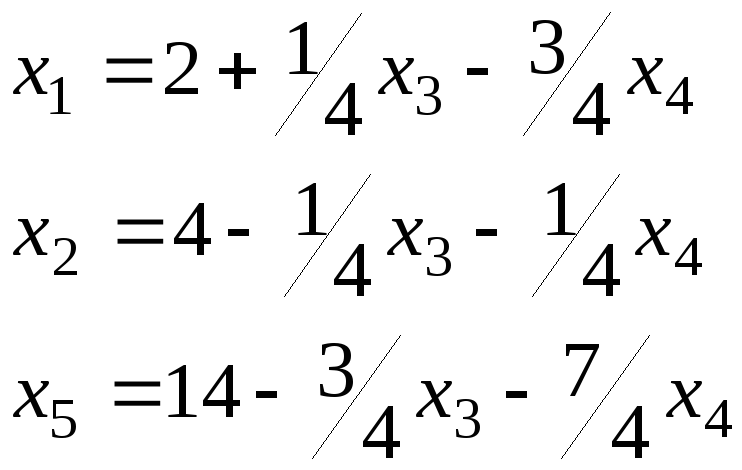
Целевую функцию запишем через свободные переменные заменив х₂.

Поскольку коэффициенты при свободных переменных положительны, то дальнейшее уменьшении функции F за счет роста свободных переменных невозможно.

Задача минимизации

х₃,х₄,х₅ – базисные переменные; х₁,х₂ – свободные переменные.

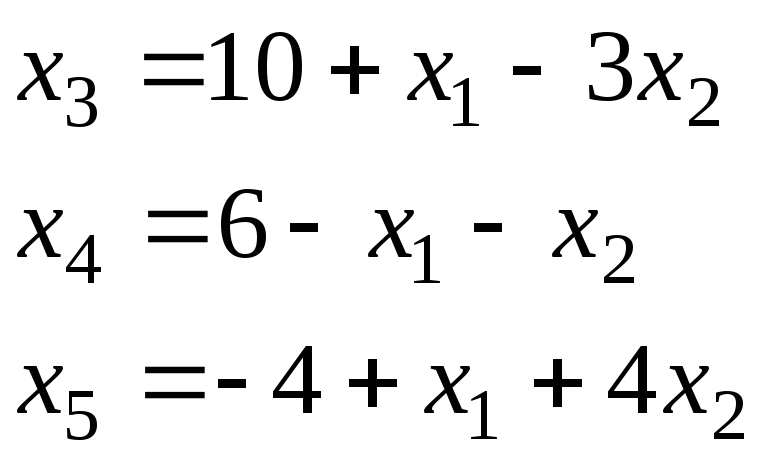
х₁⁽⁰⁾=4; х₂⁽⁰⁾=0; х₃⁽⁰⁾=14; х₄⁽⁰⁾=2; х₅⁽⁰⁾=0.

Значение целевой функции будет F⁽⁰⁾=4.

х₁,х₃,х₄ – базисные переменные; х₂,х₅ – свободные переменные.

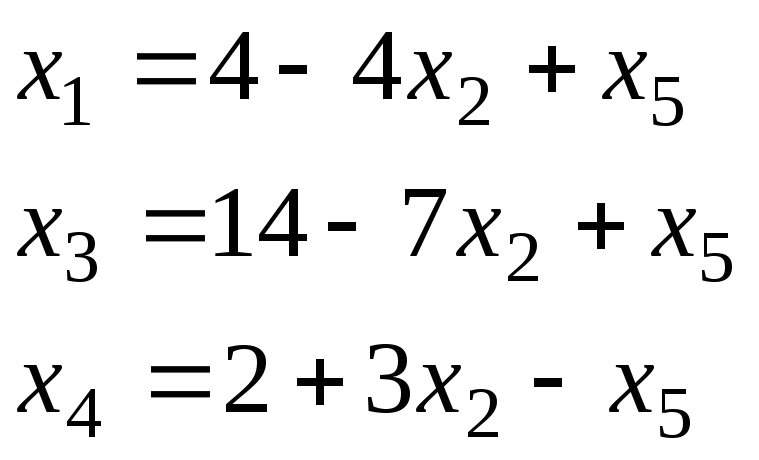
Целевую функцию запишем через свободные переменные заменив х₁.

х₅=0; х₂ увеличиваем

Получим новое опорное решение.

х₁⁽¹⁾=0; х₂⁽¹⁾=1; х₃⁽¹⁾=7; х₄⁽¹⁾=5; х₅⁽¹⁾=0.

Значение целевой функции будет F⁽¹⁾=2.

х₂,х₃,х₄ – базисные переменные; х₁,х₅ – свободные переменные.

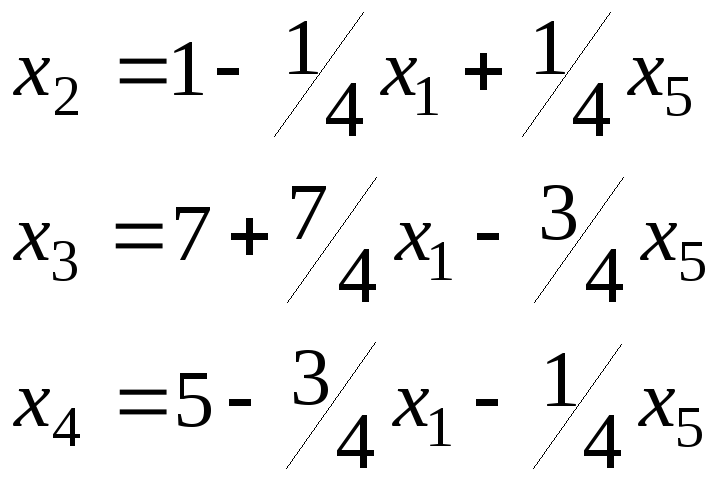
Целевую функцию запишем через свободные переменные заменив х₂.

Графический метод.

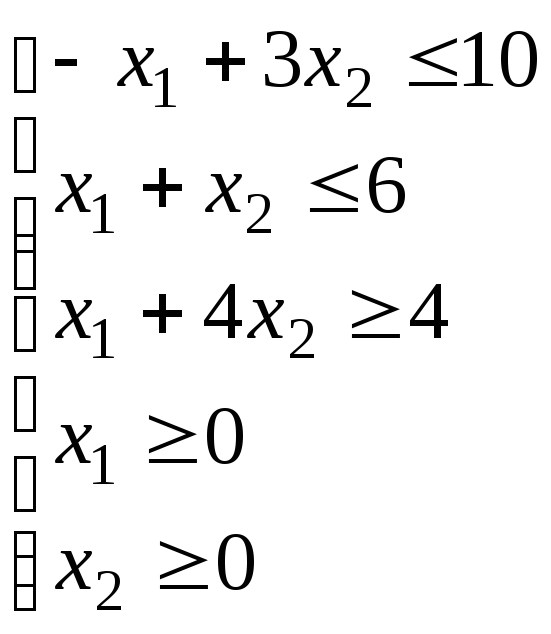
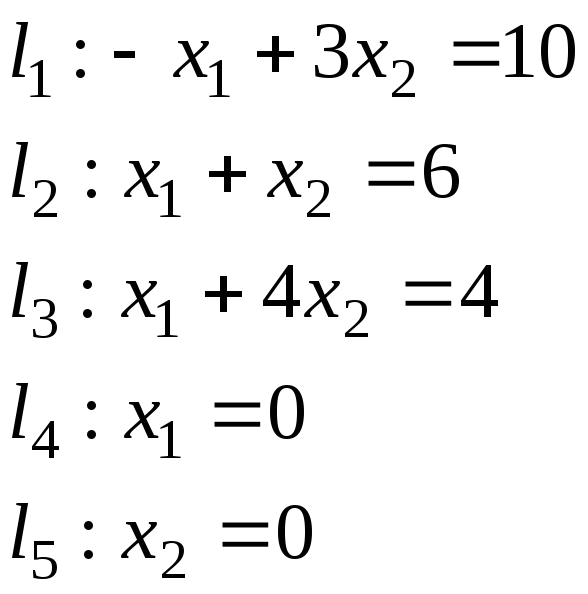
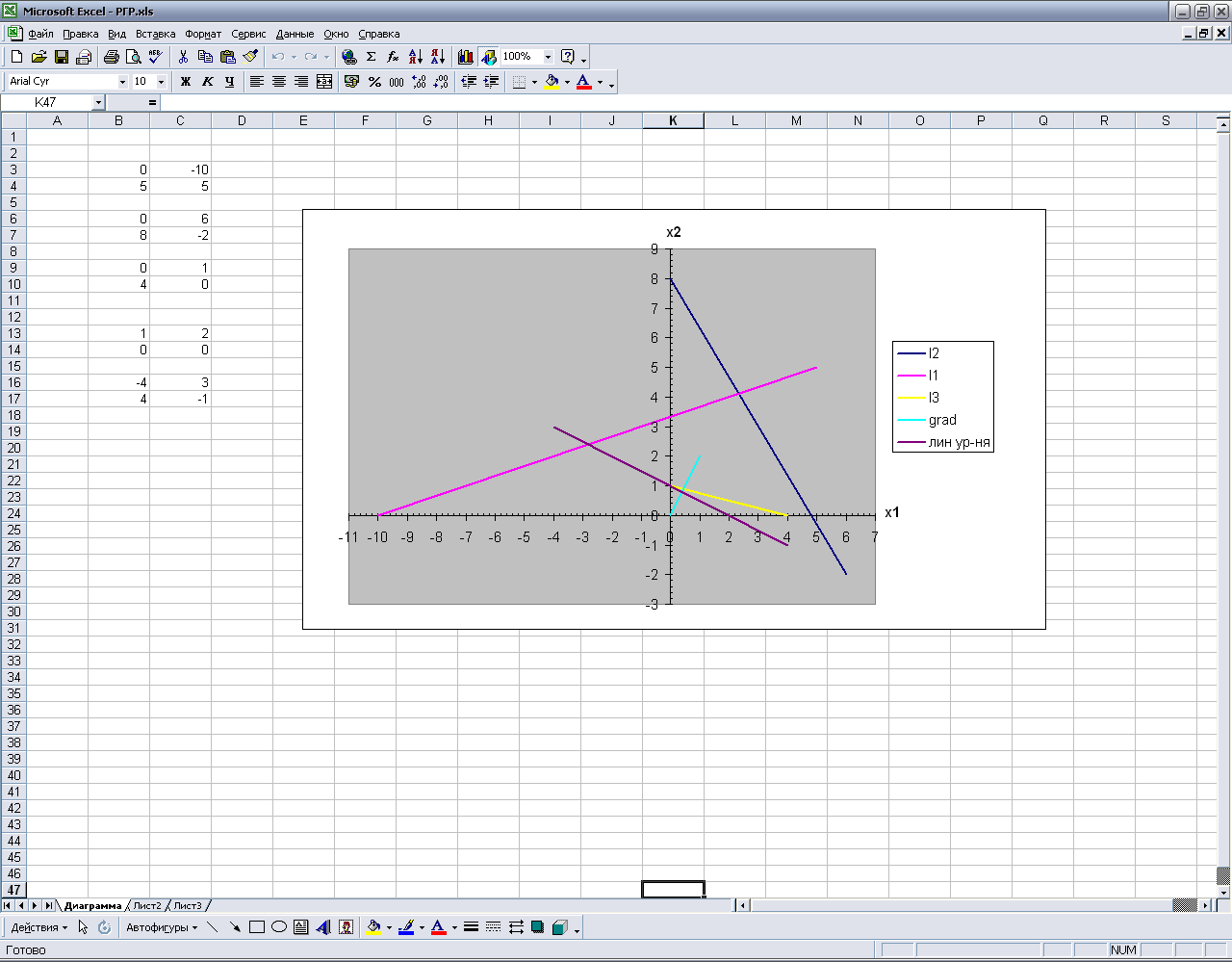
Рисунок 1 – Решение задачи графическим методом

Таким образом, минимум целевой функции достигается при х₁=0 и х₂=1 f_min=2; максимум при х₁=2 и х₂=4 f_max=10. Решив, данную задачу симплекс методом определили значение целевой функции f_min=2, f_max=10. В итоге результаты двух методов сошлись.

3