Задание для самостоятельного решения

1. Найти собственные значения и собственные векторы оператора проектирования на плоскость Охy в пространстве .

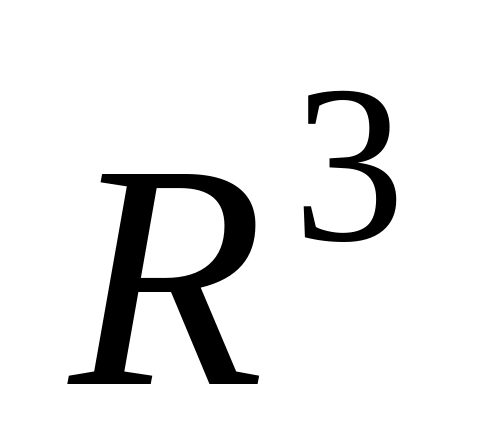2. Найти собственные значения и собственные векторы линейного оператора, заданного матрицей:

а) 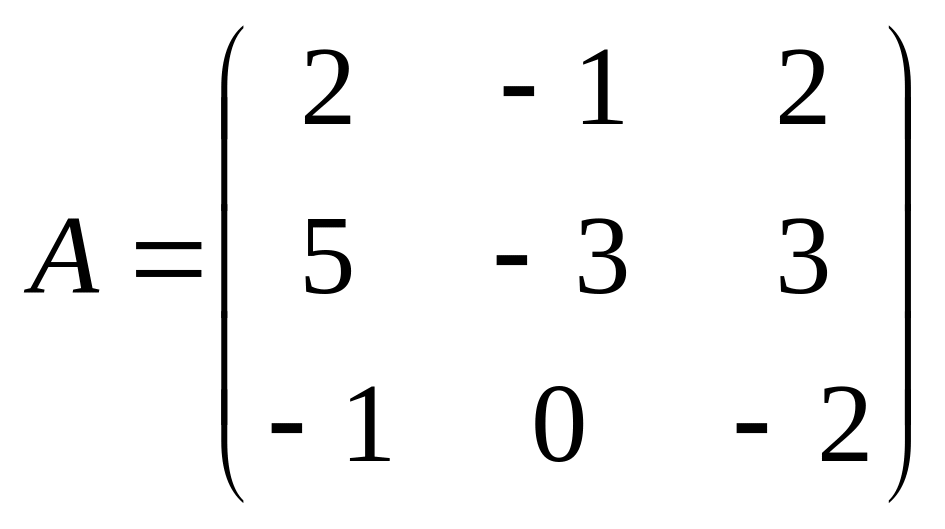б)

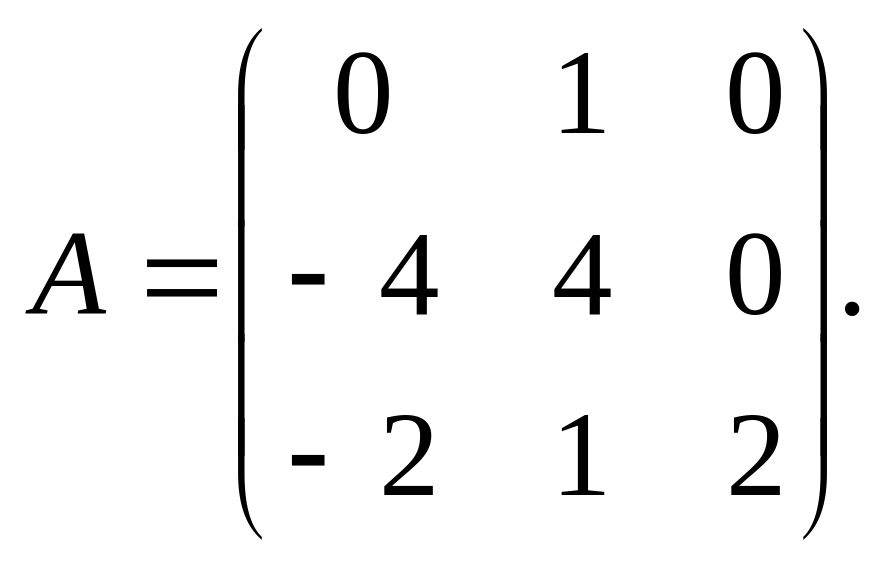
2.33. Изменение матрицы линейного оператора при преобразовании базиса

Как известно, матрица линейного оператора А однозначно определяется совокупностью образов базисных векторов. При изменении базиса матрица оператора также может изменяться. Выясним, как это происходит.

Пусть  некоторый базис в n-мерном линейном пространстве , а  другой базис того же пространства. Условимся называть базис старым, а  новым.

Запишем разложение векторов нового базиса в старом базисе

(2.33.1)

Равенства (2.33.1) можно записать в матричной форме

где 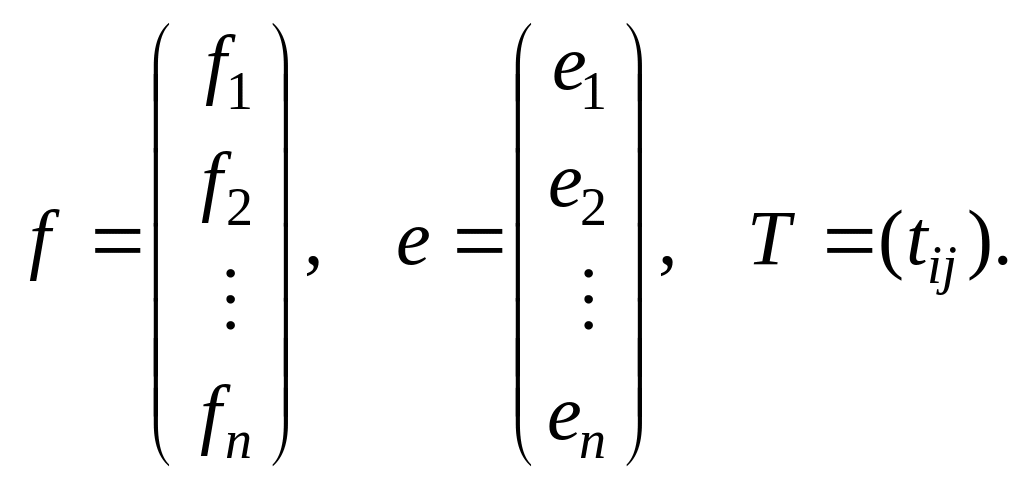(2.33.2)

Матрица является матрицей перехода от старого базиса к новому, причем, , поскольку векторы должны однозначно выражаться через .

Обозначим координаты одного и того же вектора в старом базисе через , а в новом  через . Учитывая разложение в старом и новом базисах, имеем

(2.33.2)

Используя разложения (2.33.1) в виде , перепишем равенство (2.33.2) следующим образом:

.

Из последнего следует, что

т.е. . (2.33.3)

В матричной форме соотношение (33.3) принимает вид

, (2.33.4)

где и  матрицы-столбцы с элементами и соответственно. Из формулы (2.33.4) находим

(2.33.5)

Матрицу называют контраградиентной⁷ по отношению к матрице .

Учитывая полученные формулы преобразования координат вектора при изменении базиса, найдем формулу преобразования матрицы оператора А.

(2.33.6)

Таким образом, оператору, имеющему в старом базисе матрицу , в новом базисе соответствует оператор с матрицей . Если новый базис (т.е. матрицу ) выбрать удачно, то в новом базисе матрица может принять более простой вид (см. пример из п. 2.32).

Задание для самостоятельного решения

1. Найти матрицу оператора А, заданного в базисе матрицей

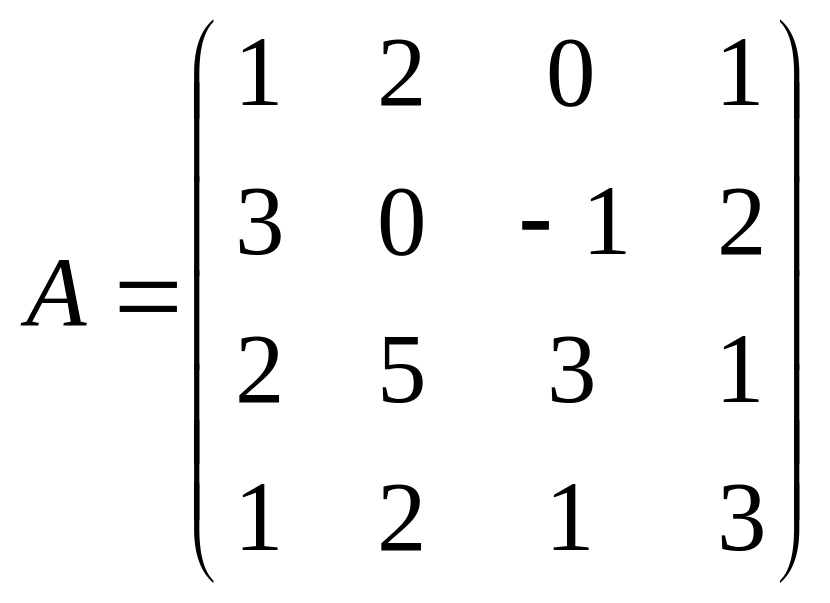
в новом базисе

2. В пространстве 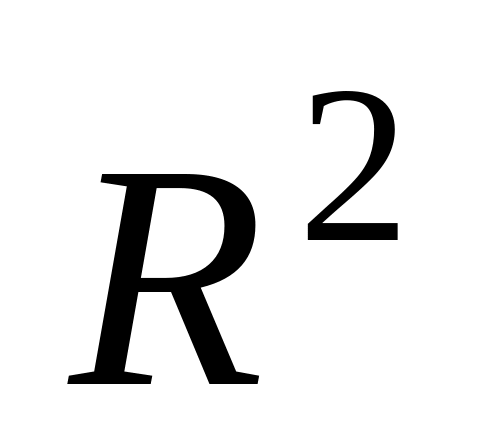оператор А в базисе 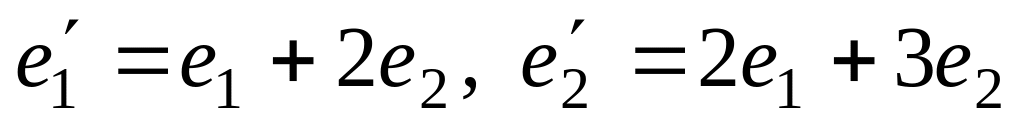имеет матрицу

Оператор в базисе имеет матрицу

Найти матрицу оператора в базисе

3. В базисе оператор А имеет матрицу

.

Записать матрицу этого оператора в новом базисе

2.34. Преобразование ортонормированного базиса в ортонормированный

Пусть теперь и  ортонормированные старый и новый базисы в евклидовом пространстве. Тогда имеем

(2.34.1)

Отсюда следует, что

т.е. матрица обладает свойством ортонормированности по строкам:

. (2.34.2)

Очевидно, что

. (2.34.3)

Запишем теперь обратное по отношению к (2.34.1) преобразование:

(2.34.4)

где .

Очевидно,что

(2.34.5)

Сравнивая (2.34.5) с (2.34.3), получим

т.е. , или

. (2.34.6)

Так как матрица ортогональна по строкам (см. (2.34.4)), то матрица ортогональна по столбцам. Таким образом, свойство ортогональности имеет место одновременно и по строкам, и по столбцам. На этом основании введем понятие ортогональной матрицы.

Квадратная матрица называется ортогональной, если для ее элементов выполняются условия

Замечательное свойство ортогональных матриц выражено формулой (2.34.6): обратная матрица для ортогональной матрицы совпадает с транспонированной матрицей.

Другое замечательное свойство ортогональных матриц сформулируем в виде следующей теоремы.

Теорема 1. При преобразовании ортонормированного базиса в ортонор –

мированный скалярные произведения векторов не изменяются.

Для доказательства рассмотрим координаты двух произвольных векторов х и у в старом и новом базисе

Связь координат вектора в старом и новом базисе определяется формулой (2.33.5), которая с учетом (2.34.6) принимает вид , т.е.

(2.34.7)

Отсюда имеем

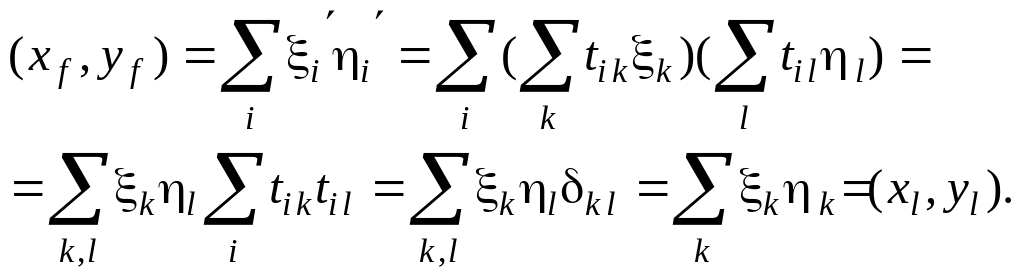
Таким образом, при ортогональном изменении базиса сохраняются модули векторов и углы между ними, т.е. пространство «поворачивается» как одно целое (слово «поворачивается» взято в кавычки, т.к. наряду с обычными поворотами возможны еще преобразования симметрии).

П р и м е р ы

1. П усть в ортогональная система координат поворачивается на угол (рис.2.21).

Так как согласно (2.34.3)

то

С помощью (2.33.4) запишем выражение координат вектора в старом базисе через его координаты в новом базисе:

2. В все выглядит аналогично:

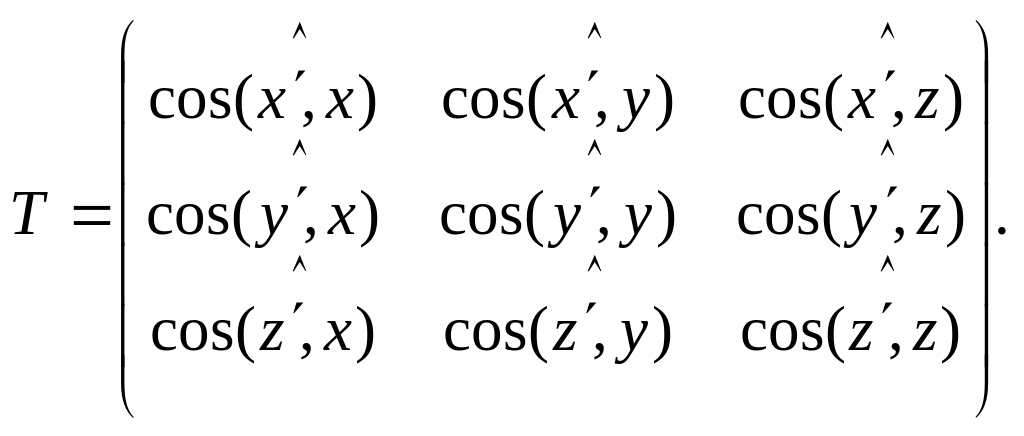
Теорема 2. Если самосопряженному оператору в ортонормированном базисе соответствует матрица , то существует ортогональное изменение базиса с матрицей , приводящее матрицу к диагональному виду:

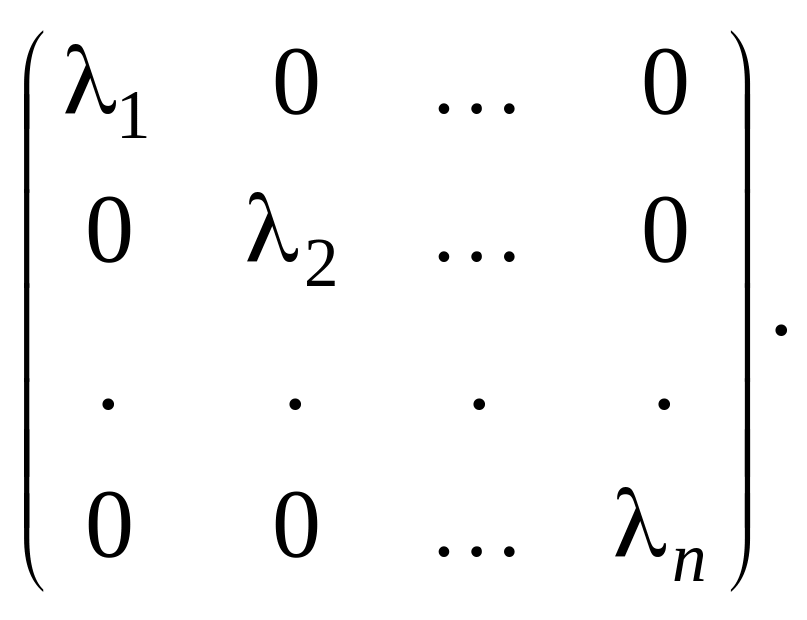
Для доказательства достаточно выбрать в качестве новых базисных векторов нормированные собственные векторы оператора. Тогда матрица Т может быть построена в соответствии с (2.34.3). В новом базисе оператор А будет задавать отображение вектора на вектор , т.е. матрица оператора в новом базисе будет диагональной.