24. Прямая линия

Уравнение прямой линии в пространстве легко записать, используя рис. 2.17:

(2.24.1)

где

 радиус-вектор произвольной точки, принадлежащей данной прямой;

 радиус-вектор некоторой фиксированной точки, принадлежащей данной прямой;

 направляющий вектор прямой, т.е. вектор, лежащий на прямой, параллельной данной;

t – произвольное действительное число (параметр).

Равенство (2.24.1) называется векторным уравнением прямой линии.

Здесь и в дальнейшем считается, что в пространстве используется ортонормированный базис и «стандартное» выражение для скалярного произведения. Очевидно, что одно векторное уравнение (2.24.1) равносильно трем следующим скалярным уравнениям:

(2.24.2)

Уравнения (2.24.2) называются параметрическими уравнениями прямой линии.

Исключая из (2.24.2) параметр t, получаем канонические уравнения прямой линии:

(2.24.3)

Вопросы

1. Как интерпретировать случай, когда в уравнениях (2.24.3) одно из чисел m, n, p окажется равным нулю ?

2. Как записать условия параллельности и перпендикулярности прямых, заданных каноническими уравнениями ?

3. Как записать уравнения прямой, проходящей через две заданные точки и

4. Как записать условия параллельности и перпендикулярности прямой линии (2.24.3) и плоскости

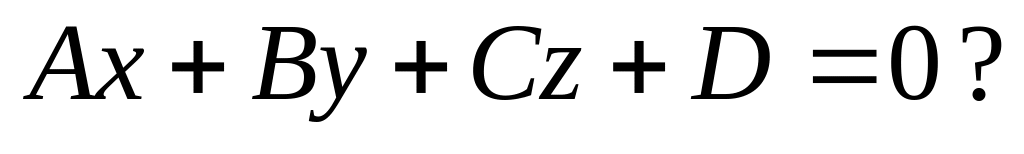
5. Как найти точку пересечения прямой (2.24.3) и плоскости

В пространстве уравнения прямой являются непосредственным обобщением соответствующих уравнений в .

Векторное уравнение:

(2.24.4)

где

Параметрические уравнения:

(2.24.5)

Канонические уравнения:

(2.24.6)

Множество

является одномерным линейным пространством. Поэтому говорят, что любая прямая в является одномерной.

Вопросы

Рассмотрим основные соотношения, связанные с прямой линией на плоскости.

1. В пространстве запишите уравнения (2.24.4) - (2.24.6).

2. Запишите уравнение пучка прямых, т.е. множества прямых, проходящих через заданную точку

3. Приведите предыдущие уравнения к виду 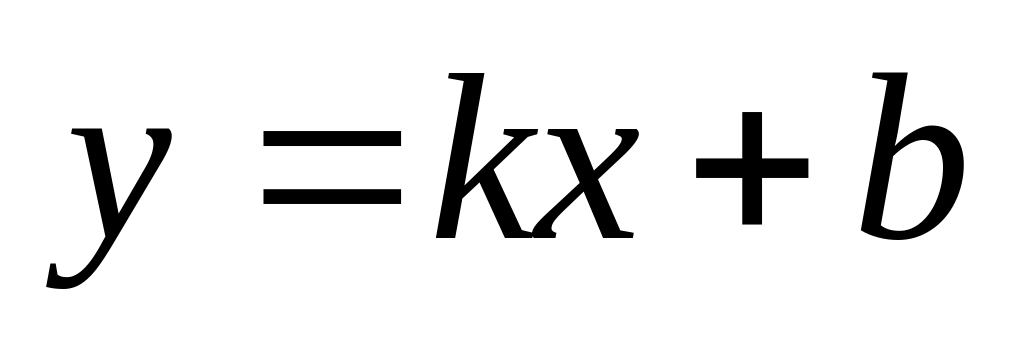, т.е. к уравнению прямой с угловым коэффициентом (напомним, что k – угловой коэффициент, b – начальная ордината прямой).

4. Как выглядят условия перпендикулярности и параллельности двух прямых на плоскости, заданных уравнениями с угловыми коэффициентами?

5. Как выразить величину угла между прямыми на плоскости через их угловые коэффициенты?

6. Как выглядит общее уравнение гиперплоскости (2.23.6) и ? Что она собой представляет? Напишите формулу для нормирующего множителя в .

Задание для самостоятельного решения

1. Напишите уравнение прямой, лежащей в пересечении плоскостей и

2. Напишите уравнение прямой, проходящей через точку перпендикулярно плоскости

3. Найдите точку пересечения прямой и плоскости

4. Выделите из пучка прямых прямую, параллельную оси 0y; 0x.

5. Из точки М(4, 5) выходит луч света под углом к оси 0x и отражается от нее. Написать уравнения падающего и отраженного лучей.

6. Лежит ли прямая в плоскости