
- •2.23. Плоскость и гиперплоскость
- •Прямая линия
- •Линейные операторы
- •2.26. Матрица линейного оператора в заданном базисе
- •Оператор проектирования (р)
- •Оператор гомотетии6 (н)
- •2.28. Геометрический смысл матрицы линейного оператора
- •2.29. Действия с операторами
- •Сложение операторов
- •Умножение оператора на число
- •Произведение операторов
- •Обратный оператор
- •Задание для самостоятельного решения
- •2.30. Сопряженный оператор. Сопряженная матрица
- •Задание для самостоятельного решения
- •2.31. Самосопряженные операторы. Симметричные матрицы
- •2.32. Собственные значения и собственные векторы линейного оператора
- •Задание для самостоятельного решения
- •2.33. Изменение матрицы линейного оператора при преобразовании базиса
- •Задание для самостоятельного решения
- •2.34. Преобразование ортонормированного базиса в ортонормированный
- •2.35. Квадратичные формы
- •2.35.1. Приведение квадратичной формы к каноническому виду
- •Задание для самостоятельного решения
- •2.35.2. Приведение общего уравнения кривых второго порядка к каноническому виду
Например,
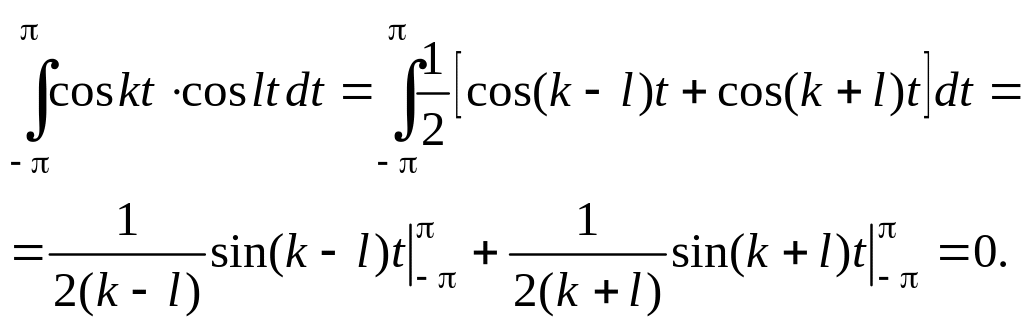
В п -
мерном евклидовом пространстве можно
ввести так называемый ортонормированный
базис
![]() :
:
![]()
где
![]() – символ Кронекера.
– символ Кронекера.
Задание для самостоятельного решения
Ортонормированный базис можно построить с помощью линейных комбинаций векторов, входящих в произвольный базис. Укажите процедуру получения ортонормированного базиса из произвольного.
Координаты вектора в ортонормированном базисе называются коэффициентами Фурье1. Коэффициенты Фурье выражаются с помощью скалярного произведения:
![]()
т.е.
![]() (2.22.3)
(2.22.3)
В ортонормированном базисе скалярное произведение всегда записывается «естественным» образом:
![]() Отсюда
ясно, что если базис не ортонормированный,
то формула для вычисления скалярного
произведения может существенно
усложниться.
Отсюда
ясно, что если базис не ортонормированный,
то формула для вычисления скалярного
произведения может существенно
усложниться.
Задание для самостоятельного решения
Подумайте, образует ли множество
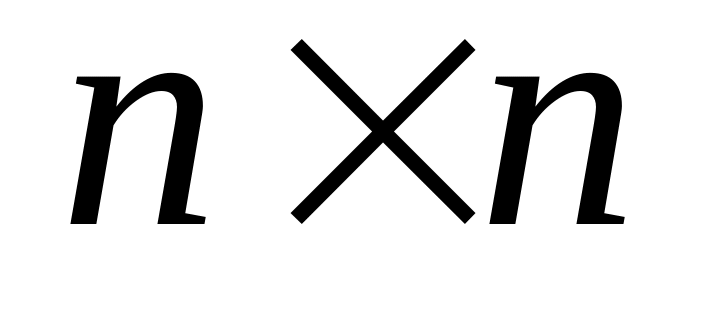 матриц:
матриц:
линейное пространство,
евклидово пространство.
Почему в евклидовом пространстве в явном виде не говорилось о коллинеарных векторах.
Приведите примеры ортонормированных базисов в
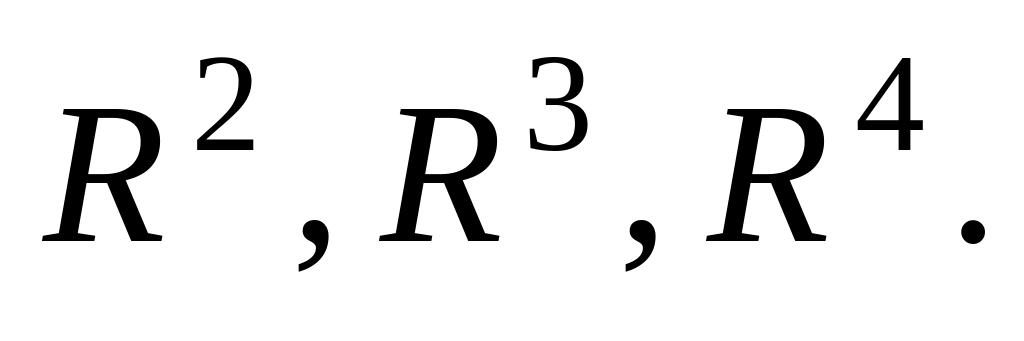
2.23. Плоскость и гиперплоскость
Рассмотрим в обычном (геометрическом) пространстве декартову систему координат. Каждая точка этого пространства отождествляется с упорядо –
ченной тройкой чисел
и возникает математическое пространство
![]() Условимся произвольную точку M(x,
y, z)
ассоциировать с концом радиуса-вектора
Условимся произвольную точку M(x,
y, z)
ассоциировать с концом радиуса-вектора
![]() (рис. 2.15). Вполне ясно, что любую плоскость
в
(рис. 2.15). Вполне ясно, что любую плоскость
в
![]() можно задать с помощью следующих величин:
можно задать с помощью следующих величин:
единичного вектора
 ,
направленного по нормали к плоскости;
,
направленного по нормали к плоскости;расстояния р от точки О до плоскости.
Тогда, очевидно,
![]()
Д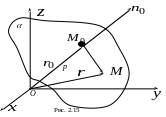 ля
того чтобы точка М лежала на заданной
плоскости, необходимо и достаточно,
чтобы вектор
ля
того чтобы точка М лежала на заданной
плоскости, необходимо и достаточно,
чтобы вектор
![]() был ортогонален
,
т.е.
был ортогонален
,
т.е.
![]()
или
![]() (2.23.1)
(2.23.1)
(2.23.1) называют уравнением плоскости в нормальном виде в векторной форме.
Вспоминая,
что
![]() из (2.23.1) получаем уравнение плоскости
в нормальном виде в координатной
форме:
из (2.23.1) получаем уравнение плоскости
в нормальном виде в координатной
форме:
![]() (2.23.2)
(2.23.2)
(2.23.2) представляет собой линейное уравнение между тремя переменными x, y, z частного вида. Если взять линейное уравнение общего вида
![]() (2.23.3)
(2.23.3)
то оказывается, что его можно свести к (2.23.2). Действительно, умножим равенство (2.23.3) на некоторое число μ :
![]()
и попробуем подобрать μ так, чтобы получилось уравнение вида (2.23.2):
![]()
Произведения
![]() можно «выдать» за направляющие косинусы,
можно «выдать» за направляющие косинусы,
если
![]()
откуда
![]()
т.е.
![]() (2.23.4)
(2.23.4)
При этом величина
![]() должна быть неположительной. Поэтому
знак у μ выбирают противоположным
знаку D.
должна быть неположительной. Поэтому
знак у μ выбирают противоположным
знаку D.
Таким образом, уравнение
(2.23.3) также есть уравнение плоскости.
Оно называется общим уравнением
плоскости. Для того чтобы перейти от
(2.23.3) к (2.23.2), достаточно умножить (2.23.3)
на так называемый нормирующий множитель
(2.23.4)
![]()
Рассмотрим вектор
![]() (2.23.5)
(2.23.5)
Так как
![]() ,
то ясно, что вектор (2.23.5), составленный
из коэффициентов при x,
y, z
, направлен по нормали к плоскости
(2.23.3) и называется нормальным вектором
плоскости.
,
то ясно, что вектор (2.23.5), составленный
из коэффициентов при x,
y, z
, направлен по нормали к плоскости
(2.23.3) и называется нормальным вектором
плоскости.
П р и м е р. Пусть дано общее уравнение плоскости:
![]() .
.
Тогда вектор
![]() ортогонален
данной плоскости.
ортогонален
данной плоскости.
Приведём уравнение плоскости к нормальному виду:
![]()
Т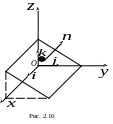 аким
образом,
аким
образом,
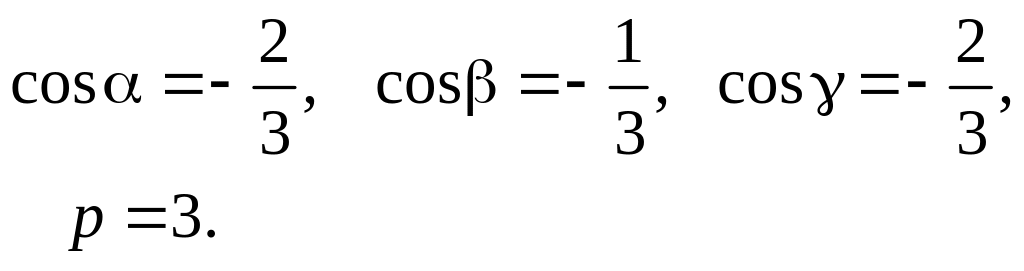
Отметим частные случаи расположения плоскости относительно системы координат:
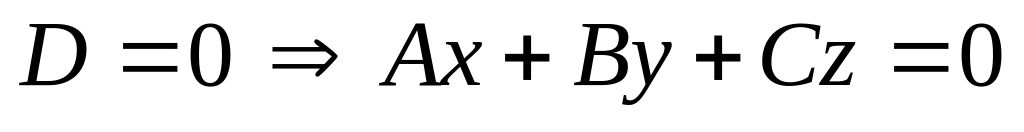 – проходит через начало координат;
– проходит через начало координат;
![]()
–параллельна оси абсцисс (рис.2.16); случаи В = 0 и С = 0 – аналогичны;
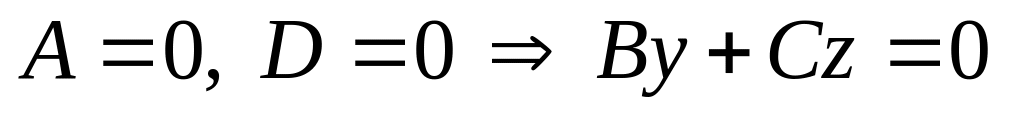 –
проходит через ось абсцисс; случаи
–
проходит через ось абсцисс; случаи
 – аналогичны;
– аналогичны;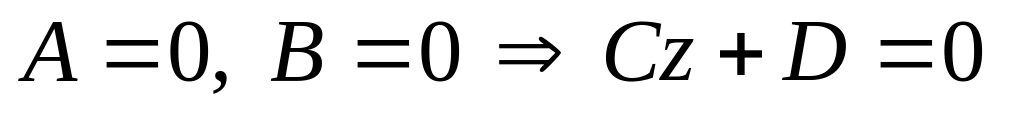 –
перпендикулярна оси аппликат; аналогичны
случаи
–
перпендикулярна оси аппликат; аналогичны
случаи
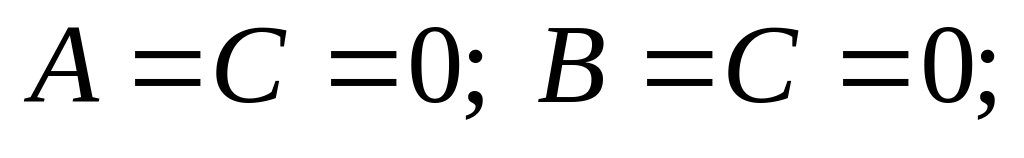
 –
уравнение координатной плоскости
0xy; аналогичны случаи
–
уравнение координатной плоскости
0xy; аналогичны случаи
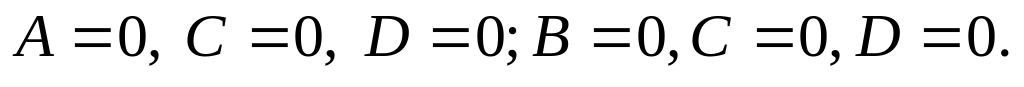

Вопросы
Как записать уравнение связки плоскостей (т.е. множества плоскостей), проходящих через заданную точку
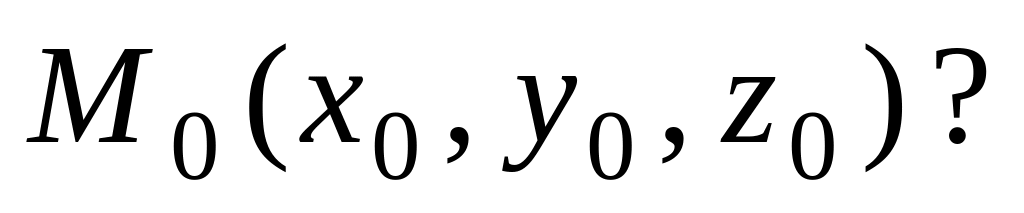
Как записать уравнение плоскости, проходящей через 3 заданные точки
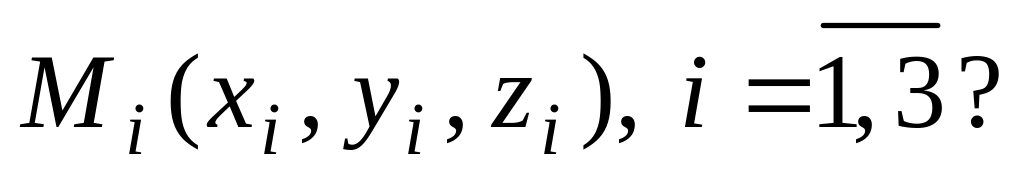
Как записать условия параллельности и перпендикулярности двух плоскостей, заданных общими уравнениями?
Как ввести понятие угла между плоскостями ? Как вычислить величину этого угла, если плоскости заданы общими уравнениями?
Что представляет собой множество
![]()
Что может представлять собой пересечение множеств
![]()
В
математическом пространстве
![]() с ортонормированным базисом, которое
при п>3 геометрической интерпретации
не имеет, вводится понятие гиперплоскости2.
Общее уравнение гиперплоскости имеет
вид:
с ортонормированным базисом, которое
при п>3 геометрической интерпретации
не имеет, вводится понятие гиперплоскости2.
Общее уравнение гиперплоскости имеет
вид:
![]() (2.23.6)
(2.23.6)
Нормальный вектор гиперплоскости
![]() (2.23.7)
(2.23.7)
Уравнение гиперплоскости в нормальном виде
![]() (2.23.8)
(2.23.8)
получается умножением (23.6) на нормирующий множитель
![]()
Вместо (2.23.8) можно записать (2.23.1):
![]()
где
![]() – радиус -вектор;
– радиус -вектор;
![]() – нормированный вектор, направленный
по нормали к гиперплоскости.
– нормированный вектор, направленный
по нормали к гиперплоскости.
В пространстве с ортонормированным базисом не представляет труда ввести многие привычные понятия: уравнение связки плоскостей; уравнение плоскости, проходящей через п заданных точек; полупространство; выпуклый3 многогранник и т.д.
Множество
![]() является линейным пространством
размерности п –1. Поэтому говорят,
что любая гиперплоскость в
имеет размерность п –1.
является линейным пространством
размерности п –1. Поэтому говорят,
что любая гиперплоскость в
имеет размерность п –1.
