3. Температуры замерзания и кипения разбавленных растворов

Опыт показывает, что температура замерзания и кипения раст­воров зависит от давления пара над ними. Еще М. В. Ломоносов об­наружил, что растворы замерзают при более низкой и кипят при бо­лее высокой температуре, чем чистые растворители. Понижение тем­пературы замерзания раствора связано с понижением давления (уп­ругости) пара растворителя над раствором.

Как известно, жидкость закипает при той температуре, при которой давление ее насыщенного пара становится равным атмосферному давлению. Так, очищенная вода при атмосферном давлении замерзает при температуре 0°С и кипит при 100°С. Стоит растворить в воде ка­кое-либо вещество, как давление ее пара понизится. Чтобы раствор закипел, необходимо нагреть его до температуры выше 100°С, т.к. только при более высокой температуре давление пара станет равным атмосферному давлению. Чем больше концентрация растворенного вещества, тем при более высокой температуре будет кипеть раствор.

Температура замерзания растворов также отличается от темпе­ратуры замерзания чистых растворителей. Известно, что жидкость замерзает при той температуре, при которой давление пара вещества в твердом состоянии становится равным давлению пара этого же веще­ства в жидком состоянии. Например, при 0°С давление пара льда (613,3 н/м²) равно давлению пара воды. Лед и вода могут одновременно сосуществовать друг с другом при температуре, которая носит назва­ние температуры замерзания.

Если взять какой-то водный раствор, то вследствие понижения дав­ления пара при 0° С он будет обладать меньшим, чем 613,3 н/м², дав­лением пара. По этой причине лед, опущенный в такой раствор, будет быстро таять. Лишь при некоторой температуре, лежащей ниже О°С, давление пара над раствором уменьшится настолько, что станет рав­ным давлению пара льда при той же температуре. Таким образом, раствор будет замерзать при более низкой температуре, чем чистый растворитель. Например, раствор, содержащий 10 г поваренной соли в 100 г воды, замерзает, не при 0°С, а при -13,6°С, морская вода – при -2,5°С.

Второй закон Рауля.

Рассмотрим простейший вывод этого закона. На рис. 4 СЛ. 5 показана диаграмма, выражающая зависимость давления насыщенного пара от температуры над чистым растворителем и над раствором.

Рис.4.

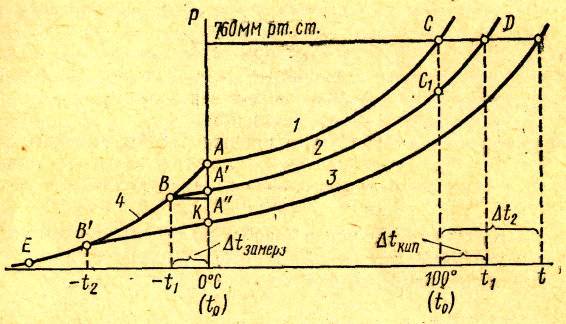
Кривая АС показывает повышение давления пара воды с увеличением темпера­туры. Кривая АВ — давление пара льда в зависимости от температу­ры, а кривая ВО показывает повышение давления пара над раствором при возрастании температуры. В точке А происходит пересечение кри­вых АВ и АС. В этой точке давление пара над раствором и давление пара льда будут одинаковыми, поэтому соответствующая данной точке температура 0°С и будет точкой замерзания чистой воды. Точку А еще называют тройной точкой, так как при этой температуре одновременно сосуществуют три фазы: жидкая (вода), твердая (лед) и газообразная (пар).

Из рис. 3 видно, что давление пара над раствором при 0°С ниже, чем у чистого растворителя (воды), но оно не равно давлению пара льда при той же температуре. Лишь при температуре, ниже нуля давление пара над раствором уменьшается настолько, что стано­вится равным давлению пара льда при той же температуре. Этому со­ответствует точка В, которая и является точкой замерзания раствора данной концентрации. При более высоких концентрациях раствора кривые, выражающие зависимость давления пара раствора от темпе­ратуры, располагаются ниже кривой АС, но параллельно ей.

Обозначим давление пара при 0° С чистого растворителя через Р₀, а раствора при температуре его замерзания через Р. Далее из точки В параллельно оси абсцисс проведем линию до пересечения с пер­пендикуляром, опущенным из точки А. Пересечение этих прямых обозначим буквой К (рис. 4).

СЛ. 6(0)Из прямоугольного треугольника ВАК определяем:

СЛ. 6(1)Из рис. 4 видно, что АК = Р₀ - Р, ВК = t- t₀ = t где t — понижение температуры замерзания раствора. СЛ. 6(2)Подставляя эти значе­ния в уравнение (****), получим:

СЛ. 6(3) Из первого закона Рауля для сильно разбавленных растворов имеем:

СЛ. 7(0)Подставив, объединив последние два уравнения, получим:

где п₀ и n — соответственно число молей воды и растворенного вещества. СЛ. 7(1)Если через W обозначить вес растворителя (воды) в граммах, а М₀ — молекулярный вес растворителя, то n₀=W/M₀, а так же K=P₀M₀/1000tg получим:

СЛ. 7(2)Выражение 1000n/W представляет собой не что иное, как моляльность раствора (m), т. е.

Подставив это выражение в уравнение (*****), получим окончательное уравнение:

t_з=Km или t_к=Еm

Это и есть математическое выражение второго закона Рауля: понижение температуры замерзания или повышение температуры кипения раст­воров прямо пропорционально его моляльной концентрации.

Коэффициент K носит название криоскопической постоянной. Она представляет собой вели­чину, характерную для данного растворителя, и показывает пониже­ние температуры замерзания, вызываемое растворением одного моля вещества (неэлектролита) в 1000 г этого растворителя.

Аналогична криоскопической постоянной константа кипения или эбулиоскопическая постоянная. Она харак­терна для данного растворителя и показывает на сколько градусов повышается температура кипения при растворении одного моля не­электролита в 1000 г растворителя.