2.4 Задачі для самостійного розв’язування

І РІВЕНЬ

2.1.1 Якої маси баласт потрібно скинути з аеростата, що рівномірно опускається, щоб він почав рівномірно підійматися з тією ж швидкістю. Маса аеростата з баластом , підіймальна сила аеростата . Вважати силу опору повітря однаковою при підйомі і спуску аеростата.

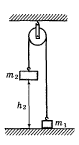
2.1.2. До нитки підвішений вантаж масою .Знайти силу натягу нитки , якщо нитку з вантажем:

а) підіймати з прискоренням ;

б) опускати з тим самим прискоренням .

2.1.3. Автомобіль масою , рухаючись рівносповільнено, зупинився через , пройшовши шлях . Знайти початкову швидкість автомобіля і силу гальмування .

2.1.4. Яку силу потрібно прикласти до вагона, що стоїть на рейках, щоб вагон почав рухатись рівноприскорено і за час пройшов шлях м? Маса вагона . Під час руху на вагон діє сила тертя , що рівна .

2.1.5. Під дією сили тіло рухається прямолінійно так, що залежність пройденого тілом шляху від часу задається рівнянням , де . Знайти масу тіла.

2.1.6. До нитки підвішений вантаж масою кг. Знайти силу натягу нитки , якщо нитку з вантажем:

а) піднімати з прискоренням м/с²;

б) опускати з тим самим прискоренням м/с².

2.1.7. Кулька масою , падаючи з деякої висоти, вдаряється об похилу площину і пружно відскакує від неї без втрати швидкості. Кут нахилу площини до горизонту . За час удару площина отримує імпульс сили . Скільки часу пройде від моменту удару кульки об площину до моменту, коли вона буде знаходитись у найвищий точці траєкторії.

2.1.8. Який кут з горизонтом складає поверхня бензину в баку автомобіля, що рухається горизонтально з прискоренням .

2.1.9. Вагон гальмує і його швидкість за час рівномірно зменшується від до . Яким повинен бути граничний коефіцієнт тертя між валізою і полицею, щоб валіза при гальмуванні почала ковзати по полиці?

2.1.10. Канат лежить на столі так, що частина його звішується зі столу, і починає ковзати тоді, коли довжина тієї його частини, що звішується, складає його довжини. Знайти коефіцієнт тертя канату об стіл.

2.1.11. На автомобіль масою т під час руху діє сила тертя , рівна . Знайти силу тяги , що розвиває двигун автомобіля, якщо автомобіль рухається з постійною швидкістю:

а) вгору з нахилом на кожні шляху;

б) вниз з таким самим нахилом.

2.1.12. Тіло лежить на похилій площині, що складає з горизонтом кут . При якому граничному коефіцієнті тертя тіло почне ковзати по похилій площині? З яким прискоренням буде ковзати тіло по площині, якщо коефіцієнт тертя ? Скільки часу необхідно для проходження при цих умовах шляху м? Яку швидкість матиме тіло в кінці шляху?

2.1.13. Невагомий блок закріплений на кінці столу. Вантажі 1 і 2 однакової маси з’єднані ниткою, що перекинута через блок. Коефіцієнт тертя вантажу 2 об стіл . Знайти прискорення , з яким рухається вантажі і силу натягу нитки . Тертям в блоці знехтувати.

2.1.14. Невагомий блок закріплено на вершині двох похилих площин, що складають з горизонтом кути і . Вантажі 1 і 2 однакової маси з’єднані ниткою, перекинутою через блок. Знайти прискорення , з яким рухаються вантажі і силу натягу нитки . Тертя вантажів об похилі площини . Тертям у блоці знехтувати.

2.1.15 Трамвайний вагон масою т рухається по заокругленню радіусом . Знайти силу бокового тиску коліс на рейки при швидкості руху .

2.1.16. Відерце з водою, прив’язане до мотузки довжиною , рівномірно обертається у вертикальній площині. Знайти найменшу швидкість обертання відерця, при якій у верхній точці вода з нього не виливається. Яка сила натягу мотузки при цій швидкості у верхній і нижній точках кола. Маса відерця з водою .

2.1.17. Вантаж, прив’язаний до нитки довжиною , описує в горизонтальній площині коло радіуса . З якою частотою обертається вантаж?

2.1.18. Диск обертається навколо вертикальної осі з частотою . На відстані від осі обертання на диску лежить тіло. Яким повинен бути коефіцієнт тертя між диском і тілом , щоб тіло не зісковзувало з диска?

2.1.19. Вантаж масою підвішений на сталевій дротині, що витримує силу натягу .На який найбільший кут можна відхилити дротину з вантажем, щоб вона не розірвалася при проходженні вантажем положення рівноваги?

2.1.20. Камінь масою прив’язаний до мотузки довжиною , рівномірно обертається у вертикальній площині. Сила натягу мотузки в нижній точці кола Н. На яку висоту підніметься камінь, якщо мотузка обривається в той момент, коли швидкість напрямлена вертикально вгору?

Рис. 2.10

ІІ РІВЕНЬ

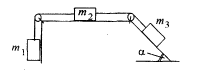
2.2.1. Через блок дуже малої маси, обертається з малим тертям,перекинута нитка, на кінцях якої прив’язані тягарці і , причому в раз ( ) більше . Вантаж піднімають на стільки, щоб вантаж торкнувся поля (рис. 2.10), і опускають. На яку висоту піднімається вантаж після того як вантаж вдариться бо підлогу, якщо висота вантажу над підлогою було ?

Рис. 2.11

2.2.2. Дошка А рухається по горизонтальному столу під дією сили натягу, прив’язаної до неї нитки. Нитка перекинута через прикріплений до столу блок і прив’язаний до іншої падаючої дошки в. (рис. 2.11):

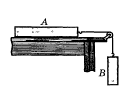
а) визначте силу натягу нитки , якщо маса дошка А рівна , маса дошка В рівна , коефіцієнт тертя . Маса блока дуже мала.

б) як зміниться відповідь, якщо дошки поміняти місцями?

Рис. 2.12

в) визначте силу, силу яка діє на вісь блока у випадку а) і б).

2.2.3. Визначте прискорення, з яким рухається вантаж масою в установці, зображеній на рис. 2.12. Тертям, маса блока і жорсткість мотузки знехтувати. Розгляньте наступні часткові випадки:

а) ;

б) ;

в) ;

г) .

2.2.4. Похилі площини 1, 2, 3 мають загальну основу (рис. 2.13)

Рис. 2.13

а) який нахил площини до горизонту, якщо час сковзання тла по цій площині менше, ніж по іншим площинам? (Розглянемо випадки коли тертя дуже мале і коли коефіцієнт тертя ).

б) який коефіцієнт тертя, якщо час ковзання при киї нахилу і час ковзання при куті нахилу рівні між собою?

Рис. 2.14

2.2.5. Крижана гора складає з горизонтом кут . По ній пускають знизу вверх камінь, який, піднявшись на деяку висоту, потім сповзає по тому ж шляху вниз. Чому рівний коефіцієнт тертя, якщо час спуску каменя в раз ( ) більше часу підйому?

Рис. 2.15

2.2.6. Визначте положення центра мас подвійного однорідного циліндра, зображеного на рисунку 2.14, де ; ; ; .

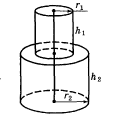
б) Визначте положення центра мас пластинки, яка має форму осьового перетину тіла, зображеного на рисунку .

2.2.7. Визначте положення центра мас фігури у вигляді точкового круглого диску радіусом , в якому вирізаний круглий отвір радіусом ,причому центр отвору лежить на відстані від центру диска (рис. 2.15).

Рис. 2.16

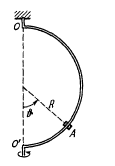
Рис. 2.17

2.2.8. На рисунку 2.16 зображено пристрій для пояснення залежності доцентрової сили від маси і відстані від осі обертання. Кулі А і В виготовлені з одного і того же матеріалу і мають діаметри 3 і 2 см. Мотузка яка з’єднує кулі має довжину . Об’ємом каналу, просвердленого всередині куль, можна знехтувати. Коефіцієнт тертя куль об стержень . Кутова швидкість обертання пристрою .

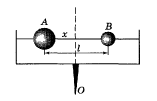
Якщо відстань кулі А від осі знаходиться в деякому інтервалі , то кулі утримуються на однаковій відстані від осі. Знайдіть і .

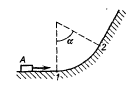
2.2.9. Невелике тіло зісковзує з вершини сфери радіуса вниз (рис. 2.17). На якій висоті від вершини тіло відірветься від поверхні сфери і полетить вниз? Тертя дуже мале.

2.2.10. Невелике тіло зісковзує вниз по похилому жолобу, який переходить в мертву петлю радіусом (рис. 18).

Рис. 2.18

а) на якій висоті випаде тіло, якщо початкова його висота рівна ? Тертя дуже мале.

б) якою повинна бути висота , щоб тіло зробило повну петлю, не випадаючи?

Рис. 2.19

2.2.11. Круглий сталевий конус з висотою і діаметром основи котиться без кочення по горизонтальній площині, здійснюючи один оберт навколо вертикальної осі протягом (рис. 2.19). Визначте силу тертя, між твірною конуса і площиною, по якій він котиться.

Рис. 2.20

2.2.12. Якщо зв’язати кінці металічного ланцюга між собою, прив’язати ланцюг до мотузки і обертають мотузку навколо вертикальної осі, то ланцюг приймає форму, близьку до кола, розташовану в площині, перпендикулярної осі обертання (рис. 2.20).

а) чи є форма ланцюга плоскою кривою?

б) приймаючи форму ланцюга за горизонтальне коло, визначте силу натягу вздовж ланцюга, якщо його маса , довжина і частота обертання .

2.2.13. Вантаж, підвішений на нитці, відводять в сторону так, що нитка приймає горизонтальне положення, і відпускають. При русі вантажу вертикальна складова його швидкості спочатку зростає, потім зменшується. Який кут з вертикаллю утворює нитка в той момент, коли вертикальна складова швидкості вантажу є найбільшою?

2.2.14. Кулька діаметром , котиться по підлозі і зупиняється через час , пройшовши відстань . Визначте коефіцієнт тертя кочення, рахуючи його постійним.

2.2.15. Брусок масою рівномірно витягують за нитку вгору по похилій площині, що складає кут з горизонтом. Коефіцієнт тертя . Знайдіть кут , який повинна складати нитка з похилою площиною, щоб натяг нитки був найменшим. Чому рівний цей натяг?

2.2.16. На похилій площині знаходиться брусок, до якого прикладена напрямлена вгору вздовж похилої площини сила , де , – сила тяжіння . Коефіцієнт тертя . При якому куті нахилу площини прискорення бруска буде мінімальним і яке це прискорення?

2.2.17. Для системи тіл, рис. 2.21, зв’язаних невагомими і розтяжними нитками, визначити натяг нитки між тілами і при умові , що початкова швидкість тіл дорівнювала нулю. Маси тіл , ; ; кут нахилу площини, на якій знаходиться тіло , до лінії горизонту , коефіцієнт тертя між тілом і відповідною горизонтальною поверхнею ; на тіла і сила тертя не діє. Тертя в блоках відсутнє.

Рис. 2.21

Рис. 2.22

2.2.18. Рис. 2.22. Визначити прискорення, з яким рухається брусок, поміщений на горизонтальну поверхню, під дією прикладених до нього сил , ; ; . Коефіцієнт тертя бруска площини ; маса бруска

а) ;

б) ;

в) .

Рис. 2.23

Прискорення вільного падіння .

2.2.19. Визначити прискорення, з яким рухаються два однакових циліндра і призма, рис. 2.23. Маса призми і кожного циліндра , кут між гранями призми задані. Вісь симетрії призми – вертикальна. Рух тіл обмежений горизонтальною поверхнею. Тертя відсутнє.

Рис. 2.24

2.2.20. Стержень, закріплений таким чином, що він може переміщатися тільки у вертикальному напрямі, нижнім кінцем спирається на гладкий клин, що лежить на горизонтальній площині. Маса стержня - , маса клина – ; кут при основі клина . Тертя відсутнє. З яким прискоренням рухається клин?

ІІІ РІВЕНЬ

2.3.1. На гладкій горизонтальній поверхні знаходяться два бруски з масами і , з’єднані ниткою. До брусків в момент часу приклали сили, протилежно напрямлені і які залежать від часу як і . Знайти, за скільки часу нитка порветься, якщо сила натягу на розрив дорівнює .

Рис. 2.25

2.3.2. В установці (рис. 2.25)маси тіл дорівнюють , і , маси блока і ниток малі, тертя в блоці відсутнє. Знайти прискорення , з яким опускається тіло і силу натягу нитки, що з’єднує тіла і , якщо коефіцієнт тертя рівний .

2.3.3. На похилу площину, що утворює кут горизонтом, помістили два бруска 1 і 2 (рис. 2.26). Маси брусків рівні і , коефіцієнти тертя між похилою площиною і цими брусками – відповідно і , причому . Знайти:

а) силу взаємодії між брусками в процесі руху;

б) кута , при якому ковзання не буде;

2.3.4. Невелике тіло пустили вгору по похилій площині, яка складає з горизонтом . Знайти коефіцієнт тертя, якщо час підйому тіла виявився в рази менший ніж час спуску.

Рис. 2.27

2.3.5. В установці (рис. 2.27) відомий кут і коефіцієнт тертя між тілом і похилою площиною. Масою блока і нитки можна знехтувати, тертя в блоці немає. Спочатку, обидва тіла нерухомі. Знайти відношення мас ,при якому тіло :

а) почне опускатися;

б) почне підніматися;

в) буда залишатися в спокої.

2.3.6. На гладкій горизонтальній площині лежить дошка масою і на ній брусок масою . До бруска прикладена горизонтальна сила, яка зростає із часом за законом , де – стала. Знайти залежність від прискорення дошки і бруска , якщо коефіцієнт тертя між дошкою і бруском рівний . Зобразити приблизні графіки їх залежності.

Рис. 2.28

2.3.7.Визначте прискорення циліндра, що ковзає по жолобу, який має вигляд двогранного кута, лінійний кут якого складає . Ребро двогранного кута нахилене до горизонту під кутом . Площини двогранного кута складають однакові кути з горизонтом. Коефіцієнт тертя між циліндром і поверхнею жолоба .

2.3.8. Сталева кулька радіуса падає з висоти без початкової швидкості на горизонтальну сталеву плиту. Опір повітря пропорційний квадрату швидкості. На яку відстань не долетить кулька до початкового положення при першому відбиванні?

2.3.9. Через нерухомий гладкий циліндр з радіусом основи перекинуто ланцюжок, довжиною . В початковий момент довжина більшого звисаючого кінця дорівнює , при цьому ланцюжок нерухомий, рис. 2.28. Знайти закон руху кінця ланцюжка , якщо його відпустити.

2.3.10. На скільки зміниться дальність польоту невеликого тіла масою , кинутого під кутом до горизонту з початковою швидкістю за рахунок опору повітря, якщо опір пропорційний швидкості (коефіцієнт пропорційності рівний ).

2.3.11. На ідеально гладкій похилій площині з кутом нахилу до горизонту знаходиться дошка масою . Куди і з яким прискоренням повинен бігти по дошці хлопчик масою , щоб дошка залишилася на місці. При якому мінімальному коефіцієнті тертя між дошкою і підошвами черевиків це можливо?

2.3.12. На горизонтальній дошці є виступ висотою , в кий упирається циліндр радіусом , що лежить на дошці. З яким максимальним прискоренням можна рухати дошку в горизонтальному напрямі, щоб циліндр не перекотився через виступ?

2.3.13. Два вантажі масами і з’єднані ниткою довжиною . Нитка пропущена через кільце, закріплене на вертикальному стержні. З якою кутовою швидкістю потрібно обертати стержень, щоб нитка була зігнута під кутом .

Рис. 2.29

2.3.14. Невелику шайбу поклали на похилу площину, що утворює кут з горизонтом (рис. 2.29), і надали початкову швидкість . Знайти залежність швидкості шайби від кута , якщо коефіцієнт тертя і в початковий момент .

Рис. 2.30

2.3.15. Муфточка може вільно ковзати вздовж гладкого стержня, вигнутого у формі півкільця радіуса (рис. 2.30). Система почала обертатися з сталою кутовою швидкістю навколо вертикальної осі . Знайти кут , що відповідає стійкому положенню муфточки.

2.3.16. Невелику кульку масою , підвішену на нитці, відвели в бік так, що нитка утворила прямий кут з вертикаллю, а потім відпустили. Знайти:

а) модуль повного прискорення кульки і силу натягу нитки як функції кута її відхилення від вертикалі;

б) силу натягу нитки в момент, коли вертикальна складова швидкості кульки максимальна;

в) кут відхилення нитки в момент, коли повне прискорення кульки горизонтальне.

2.3.17. Невелике тіло починає ковзати з вершини гладкої сфери радіуса . Знайти кут між вертикаллю і радусом0вектором, що характеризує положення тіла відносно центра сфери в момент відриву від неї, а також швидкість тіла в цей момент.

2.3.18. Автомобіль рухається зі сталим тангенціальним прискоренням м/с² по горизонтальній поверхні, описуючи дугу радіусом м. Коефіцієнт тертя між колесами автомобіля і поверхнею . Який шлях пройде автомобіль без ковзання, якщо в початковий момент часу його швидкість дорівнює нулю?

Рис. 2.31

2.3.19. Невелике тіло ковзає по гладкій горизонтальній поверхні вздовж вертикальної стінки, що має вигляд як на рис. 2.31 (вигляд зверху). Заокруглена частина траєкторії тіла є дугою з кутом . Знайти швидкість тіла в точці 2, якщо в точці 1 м/с і коефіцієнт тертя між тілом і вертикальною стінкою .

2.3.20. Через закріплений блок перекинута нитка, до кінців якої прикріплені вантажі масами і . Між ниткою і блоком є тертя таке, що нитка починає ковзати по блоку, коли . Знайти:

а) коефіцієнт тертя;

б) прискорення вантажів, якщо .