Лекции по ТП / Полустат+дин.структуры

9

Полустатические структуры

Определения этих структур данных основаны на понятии списка или списковой структуры.

Списком называется линейно-упорядоченная последовательность элементов данных E(1),E(2)…E(n), где n>0,причем каждый элемент E(i) характеризуется одним и тем же набором полей. Такой список называют линейным списком из-за линейной упорядоченности элементов. Упорядоченность элементов списка может быть задана неявно путем последовательного расположения его элементов как в логической структуре, так и в памяти ЭВМ (т.е физической структуре данных). Список с таким неявным заданием упорядоченности в логической и физической структурах называют еще последовательным линейным списком. С другой стороны, упорядоченность может задаваться явно путем помещения в каждом элементе E(i) указателей или связок, в которых помещается адрес последующего или предыдущего элемента списка. Такие списки называют связными списками и о них мы буде мы говорить позже.

При n=const и соответствующем выборе элемента данных, последовательный линейный список сводится к вектору, к массиву , записи или таблице. Так, вектор может быть определен как последовательный линейный список, в котором каждый элемент-скаляр одного и того же типа.

При n=Var последовательный линейный список представляет собой структуру, не обладающую свойством постоянства. Однако, хотя n=Var, максимальное значение n задается явно и ограничивает длину списка. Такие структуры называют полустатические.

Полустатические структуры данных- это последовательные линейные списки с переменной длиной, ограниченной фиксированной максимальной величиной и с ограниченным доступом. К таким структурам относятся стеки и очереди. Есть еще деки, но они менее распространены и на них останавливаться не будем.

Стек - такой последовательный линейный список с переменной длиной, включение и исключение элементов из которого выполняется только с одного конца списка. Известно и другое название стека – магазин. Иногда стек называют еще очередью, функционирующей по принципу LIFO (Last- In-First- Out –последним пришел – первым вышел).

Emax

En

En-1

…

E1

Верхняя граница стека

Свободные слоты

Вершина стека, с ней связан указатель стека = адрес последнего занятого элемента стека

Нижняя граница стека

Рис.1 Логическая структура стека

Физическая структура стека может быть изображена следующим образом:

ST – имя стека

Адрес верхней границы

Указатель вершины

Адрес нижней границы

Описание элемента

Ячейки оперативной памяти ЭВМ

Рис.2 Физическая структура стека

Для включения нового элемента в стек сначала изменяется значение указателя вершины стека на длину элемента стека, а затем по значению этого указателя помещается новый элемент стека. При исключении элемента стека сначала прочитывается информация из вершины стека по значению указателя, а затем значение указателя уменьшается на величину длины элемента стека.

Другими операциями над стеком, кроме включения и исключения элемента является очистка стека и проверка объема стека, т.е. числа элементов в стеке.

Стеки привлекательны тем, что, во-первых, машинные команды работы со стеком очень короткие – они либо не требуют операндов вообще, либо используют один операнд, во-вторых, с применением стека легко реализуются вычисления сложных арифметических выражений. Программа вычисления таких выражений записываются в обратной польской нотации – когда сначала записываются в стек операнды, а потом знак операции, например, выражение a+b в этой записи выглядит как ab+, а программируется как:

рush a, ; протолкнуть в стек значение а

push b, ; протолкнуть в стек значение в

add ; вытолкнуть из стека 2 значения, сложить их и протолкнуть результат в стек.

Для хранения стека в памяти ЭВМ отводится сплошная область памяти ограниченного объема. Если в процессе заполнения стека указатель выходит за отведенные границы стека, то происходит переполнение стека и включение нового элемента становится невозможным.

Рассмотрим пример применения стека для выполнения рекурсивной процедуры. Рекурсивной называется такая процедура, которая содержит обращение к самой себе, например, вычисление факториала.

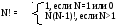
На языке Паскаль вычисление факториала может быть описано следующей функцией:

Function answer(n: word) : longint;

Fact: longint:

begin

if n>1 then fact: = n* answer (n-1) else fact : = 1;

answer: = fact;

end;

Допустим, фрагмент программы:

m:=3:

Factorial:=answer(m);

next: следующий оператор.

Выполнение действий в такой программе может быть проиллюстрировано рисунком 5 и таблицей 1.

Стековая память используется при трансляции входных языков и обмене между программными компонентами процессора.

Рисунок 4 - Выполнение рекурсивной функции с использованием стека

Таблица 1 – Описание действий и содержимого стека при выполнении рекурсивной функции

Вход	Результаты	Следующие действия
Первый	1. Выполняется пролог 3 Адрес метки NEXT Стек: Указатель 2. Выполнение тела: N=N–1; N=2	Обращение процедуры самой к себе ANSWER(N)
Второй	1. Выполнение пролога 2 Адрес метки A 3 Адрес метки NEXT Стек: Указатель 2. Выполнение тела: N:=N–1; N=1	Обращение процедуры самой к себе ANSWER(N)
Третий	1. Выполнение пролога: 1 Адрес A 2 Адрес A 3 Адрес NEXT Стек: указатель 2. Выполнение тела: ANSWER=1 3. Выполнение эпилога (первое): Стек: указатель 2 Адрес A 3 Адрес NEXT ANSWER=1*1=1 4. Выполнение эпилога (второе): 3 Адрес NEXT Стек: указатель ANSWER=2 5. Выполнение эпилога Стек – пуст ANSWER=6	Первое обращение к метке A Первый возврат на метку A Второй возврат на метку A Возврат на метку NEXT

Очередь – такой последовательный список с переменной длиной, включение элементов в который происходит с одной стороны, а исключение с другой стороны списка.

Очередь функционирует по принципу – FIFO (First-In-First-Out-первым пришел, первым вышел).

Для индикации начала и конца очереди организуются 2 указателя: схема простейшей очереди будет следующая:

Указатель P2

A1

A2

Amax

Указатель P1

Из схемы следует: для очереди выделяется фиксированный участок памяти ЭВМ, в котором, как правило, заняты в каждый момент времени лишь некоторые слоты. Указатель P1 является адресом первого (начального), слота очереди, P2 – адресом первого свободного слота очереди.

При включении в очередь pзапись вносится по адресу P2, затем значение указателя P2 изменяется (передвигается на 1 элемент очереди), т.е. значение P2 увеличивается на длину элемента очереди.

При исключении из очереди извлекается элемент, адресуемый указателем P1, и после этого указатель P1 перемещается к следующему слоту, т.е. его значение увеличивается на длину элемента очереди.

Возможны и другие операции с очередью: очистка и проверка длины.

Очевидно, что в процессе включения элементов неизбежно возникнет состояние переполнения очереди - выход указателя P2 за пределы Amax. Такой недостаток схемы, может быть устранен, если после достижения указателем P2, значение Amax переводить указатель P2 на адрес A1, если слот A1 пуст. Организованная таким образом очередь называется кольцевой. В ней возможны любые соотношения указателей P1 и P2: P1>P2, P1=P2, P1<P2. P1=P2 – очередь пуста. Используется при обмене данными между устройствами ЭВМ.

Линейные динамические структуры.

Динамическая структура имеет следующие основные признаки:

1.Непостоянство и непредсказуемость размера (числа элементов) структуры в процессе ее обработки. Число элементов динамической структуры может изменяться от 0 до некоторого значения, определяемого спецификой задачи или доступным размером машинной памяти.

2. Отсутствие физической смежности элементов структуры в физической памяти. Логическая последовательность элементов задается в явном виде с помощью одного или нескольких указателей или связок, хранящихся в самих элементах. Следовательно, память, занимаемая динамической структурой не является непрерывной и может быть хаотически разработана в области памяти.

Часто динамические структуры физически представляются в форме связных списков.

Связный список – такая структура, элементами которой служат записи с одним и тем же форматом, связанные друг с другом с помощью указателей, хранящихся в самих элементах списка.

В односвязном линейном списке каждый элемент состоит из двух различных по назначению полей: содержательного и поля указателя.

Логическая структура может быть изображена так:

Указатель начала

Указатель

данные



данные

Указатель

данные

 -пустой указатель, означает конец списка.

Физическая структура списка может быть такой :

Линейный двусвязный список отличается от односвязного тем, что каждый его элемент содержит два указателя, один из которых (прямой указатель) адресует следующий элемент в списке, а другой (обратный указатель) - адресует предыдущий элемент списка.

Логическая структура двусвязного списка:

Указатель начала

Указатель конца

….

В первой записи пустым является обратный указатель, а в последней – прямой.

В этом случае доступ к списку возможен как с начала списка, так и с его конца.

Включение списка и исключения элемента из списка осуществляется путем корректировки указателей.

Схематично покажем включение в односвязный список нового элемента между двумя существующими элементами списка. Чаще всего местоположение нового элемента определяется по назначения ключа:

В этом случае значение L2 записывается в поле указателя включаемой записи значение поля указанной записи, после которого включается новый элемент, изменяется на L_N ,,окончательная логическая структура будет следующей:

D₁ L₁

D₂ L_N

D_N L₂

D₃ L₃

D₄ L₄

Исключение из списка может быть так:

В этом случае поле указателя записи, после которого удаляется элемент изменяется на значение адреса, следующего за исключаемым элемента списка (L2L3). Оконченная логическая структура обновленного списка:

D₁ L₁

D₂ L₃

D₄ L₄

Вернемся к двусвязному списку. Такой список может и не быть линейным, если второй указатель каждого элемента списка является не обратным, а используется, например, для указания другого линейного списка.

К таким структурам приводит экономное представление разреженных матриц.

A1				A2		A3
		A4			A5
	A6		A7

Описание очередной строки матрицы  количество ненулевых элементов.

Указатели списка значений элементов  адрес списка значений элементов.

Получим следующую логическую структуру разреженной матрицы: