12

Министерство общего и профессионального образования

Российской Федерации

КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

и м. А.Н. ТУПОЛЕВА

Кафедра теоретической радиотехники и электроники

Е.Ф. Базлов В.A.Михайлов.

Основы теории цепей исследование частотных характеристик цепей первого порядка

Методические указания к лабораторной работе № 103 (EWB)

Казань 2001

Цель работы исследовать передаточные частотные характеристики RC–, RL– цепей первого порядка (с одним реактивным элементом).

Основные понятия, расчетные формулы и определения

К простейшим RC–, RL– четырехполюсникам ( четырехполюсникам первого порядка) относятся четырехполюсники, содержащие один реактивный элемент (емкость C или индуктивность L). Они называются также интегрирующими RC–, RL– (рис.2,a) и дифференцирующими RC–, RL–четырехполюсниками (рис.2,б).

Передаточные частотные характеристики четырехполюсников.

Среди передаточных параметров четырехполюсников основным является комплексный коэффициент передачи по напряжению K(j). Он представляет собой отношение комплексного выходного напряжения и комплексного входного напряжения четырехполюсника:

(1)

где  модуль комплексного коэффициента передачи по напряжению K(j);

 действующие (амплитудные) значения выходного и входного гармонических напряжений;

()=(_u2)- (_u1) аргумент комплексного коэффициента передачи K(j);

(_u2), (_u1) начальные фазы выходного и входного гармонических напряжений.

Зависимости модуля K() и аргумента () комплексного коэффициента передачи от частоты называются соответственно амплитудно-частотной (АЧХ) и фазо-частотной (ФЧХ) характеристиками цепи.

Расчет и экспериментальное исследование частотных характеристик проводят в установившемся синусоидальном режиме, который реализуется с помощью гармонического входного сигнала. Рассматриваемые в работе четырехполюсники могут быть представлены обобщенной комплексной схемой замещения в виде Г-образного четырехполюсника (рис.2).

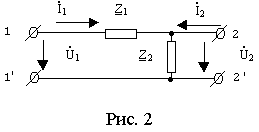
В режиме холостого хода комплексный коэффициент передачи по напряжению такого четырехполюсника определяется формулой

(3)

Он зависит от вида комплексных сопротивлений Z₁ и Z₂ и от сопротивления нагрузки со стороны зажимов 22'. Цепи такого типа (делители напряжения) рассмотрены в предыдущей работе.

На частотах входного гармонического сигнала, когда Z₁Z₂, модуль коэффициента передачи близок к 1, т.е. K()=1.

Если Z₁=Z₂, то K()=0,5. На частотах, когда Z₁>>Z₂, коэффициент передачи стремится к нулю.

Используя выражение (3) для конкретной схемы делителя напряжения (рис.2), т.е. подставив значения Z₁ и Z₂, можно получить выражения АЧХ и ФЧХ K(j).

В таблице 1 приведены выражения и графики частотных характеристик интегрирующих и дифференцирующих RC и RLцепочек.

Р ассмотрим в качестве примера интегрирующую RCцепь (рис.1,а). Подставляя в выражение (2) Z₁=R, Z₂=1/jC и выполняя преобразования, получим аналитическое выражение комплексного коэффициента передачи по напряжению K(j):

О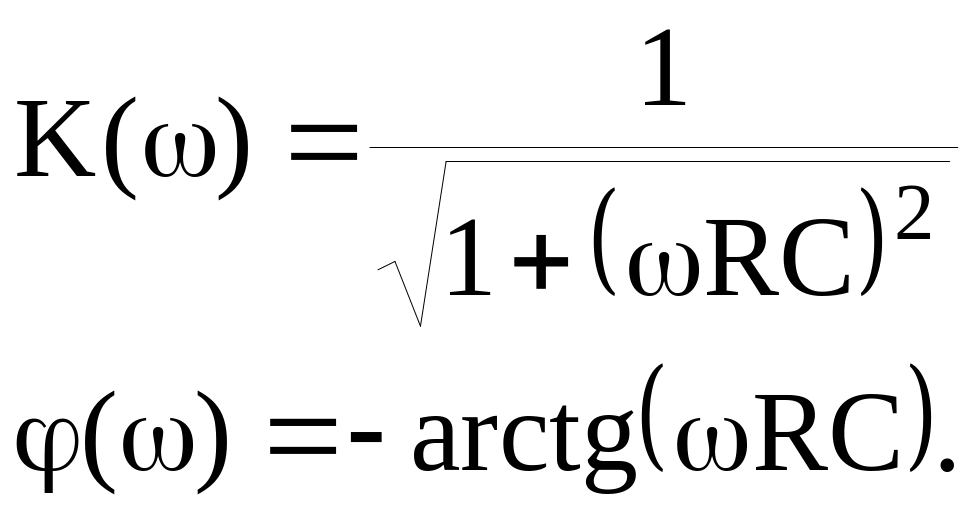 тсюда:

АЧХ 

ФЧХ 

Модуль K(j) и аргумент () комплексного коэффициента передачи зависят от частоты, т.к. в цепи имеется емкость, сопротивление которой зависит от частоты.

Расчет частотных характеристик всегда проводят в определенном диапазоне частот, который выбирают по выражению АЧХ. Для цепей первого порядка модуль коэффициента передачи по напряжению можно представить в виде:

где a безразмерный параметр (обобщенная расстройка), который зависит от частоты . В нашем примере a=RC.

Наиболее характерные свойства функции K() проявляются в диапазоне частот, в котором параметр a меняется в пределах: 0.1<a <10.

Граничные значения параметра a: a₁=0,1 и a₂=10 позволяют оценить нижнюю f₁ и верхнюю f₂ частоты диапазона, в котором нужно считать частотные характеристики. Для интегрирующей RC–цепочки:

a₁=₁RC=2f₁RC=0,1; f₁=0,1/2RC=f_min, a₂=₂RC=2f₂RC=10; f₂=10/2RC=f_max.

Таким образом, частотные характеристики интегрирующей RC-цепочки достаточно рассчитать в диапазоне частот f₁f₂. Число точек по оси частот на график следует брать 1020.

На рис.3 изображены АЧХ и ФЧХ коэффициента передачи по напряжению интегрирующей RCцепочки: R=10000 Ом, C=15000 пФ, f₁=100 Гц, f₂=10000 Гц.

Ф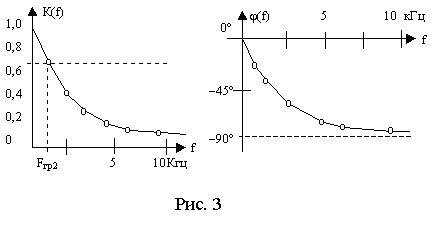 орму частотных характеристик, изображенных на рис. 3, можно объяснить следующим образом. На частоте f=0 сопротивление емкости Z_C=1/jC= и входной ток I₁=0. Поэтому падение напряжения на сопротивлении R равно нулю – U_R=I₁R=0, а выходное напряжение U₂ равно входному U₁ и коэффициент передачи по напряжению K(0)=U₂/U₁=1, а аргумент коэффициента передачи  (0)=₂ ₁=0. На рис.4, а) изображена схема замещения RCцепочки для f=0. С ростом частоты сопротивление емкости уменьшается, а резистора R остается постоянным. Ток I₁ будет увеличиваться и падение напряжения U_R=I₁R тоже будет расти. На основании второго закона Кирхгофа (см. (2)) выходное напряжение U₂=U_C при этом будет уменьшаться, и коэффициент передачи будет меньше единицы. Напряжение на емкости в RCцепочке отстает по фазе от тока, протекающего через нее.

П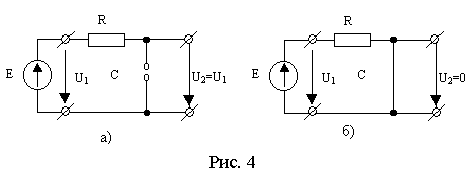 оэтому выходное напряжение будет отставать по фазе от входного и аргумент коэффициента передачи будет иметь отрицательное значение. В пределе, когда f=, сопротивление емкости Z_C=1/C=0, и коэффициент передачи K()=0. Схема замещения цепочки изображена на рис. 4, б). Так как на частоте f= входной ток определяется только сопротивлением R (I₁=U₁/R), то фаза тока I₁ совпадает с фазой входного сигнала U₁. Напряжение на емкости отстает по фазе от тока на 90. Таким образом, аргумент коэффициента передачи будет равен -90.

Проведенные рассуждения можно применить и к другим видам RC, RLцепочкам. Проделайте это самостоятельно.

Полоса частот, в пределах которой коэффициент передачи изменяется от максимального значения K_max до уровня K_max/1,41=0.7K_max называется полосой пропускания S. Частоты, соответствующие границам полосы пропускания, называются граничными частотами f_гр. Следовательно, полоса пропускания равна:

S=f_гр2f_гр1

В рассматриваемом примере при f_гр1=0 K(0)=1=K_max. Если решить уравнение

т о можно определить вторую граничную частоту f_гр2. Тогда, полоса пропускания S равна:

Значения граничных частот зависят от вида цепи и параметров элементов. Для интегрирующей RCцепочки с увеличением R и C полоса пропускания уменьшается.