3. Показатели надежности невосстанавливаемых объектов.
Показатель надежности-количественная хар-ка одного или нескольких св-в составляющих надежность.
1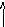
.
F(t)-неубывающая
ф-ия; в t=0
F(0)=0
-статистический
показатель 1
,
где N-число
объектов пост. на испытание, N(t)-число
объектов отказавших к моменту времени
t.
2
.
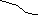-ф-ия
надежности 1
,
,
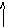t
3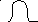
.
Плотность распределения
t
-интервал
времени,
-число
отказ. объектов заt
4.
-вер-ть
отказа объекта к моменту времениt1,
5.
-вер-ть
безотказной работы объекта к моменту
времениt1
,
6.
«+» а) характеризует изменения надежности во времени, б) вер-ть безотказной работы входит в показатели эффективности сложн. устр-в, в) просто опред-ся расчетным путем до изготовления объекта г) по данному показателю оптимизируется структура объектов д) используется как для элементов, так и для сложн устройств «-» а) по ней трудно определить другие харки надежности б) хар-ет работу устройства до первого отказа
7. Интенсивность отказа: λ(t)-условная плотность вер-ти отказа в момент времени t при условии, что до этого момента отказы не возникали.
-
условная вер-ть безотказной работы
8.
Средняя наработка до отказа:
.
При экспотенц. законе распределения
вер-ть безотказной работы на интервале
зависит только от длины интервала и не
зависит от времени предшествующей
работы объекта.
6. Простейший поток отказов. Его свойства.
Условия существования потока отказов: 1) элементы объекта работают одновременно 2) отказы носят мгновенный характер 3) отказ одного элемента ведет к отказу всей системы 4) старение отсутствует
Сумма
простейших потоков образует простейший
поток с параметрами
7. Нестационарный пуассоновский поток. Поток Эрланга.
Это поток, не удовлетворяющий условию стационарности. Наблюдается в процессе приработки устройств, в сложных объектах, в которых элементы работают не одновременно и в резервированных объектах. Условия существования: 1)отказы элементов носят мгновенный характер 2) отказ одного элемента ведет к отказу всей системы 3)старение элементов отсутствует
,
где
-
параметр потока отказов.
Поток Эрланга. Образуется в результате разряжения простейшего потока событий путем отбрасывания некоторых из них.
Если в объекте парируется каждый 2-ой отказ, то образуется поток Эрланга 2-го порядка. Если 2 из 3-х событий, то 3-го порядка. Потоки Эрланга встречаются в объектах, где имеются средства разряжения потока отказов: а)система контроля, б)аппаратное резервирование, в)временное резервирование, г) изменение конфигурации объектов.
8. Показатель надежности восстанавливаемых объектов.
В восстанавливаемых объектах наблюдается 2 потока:
1)
поток отказов; параметр
-
среднее кол-во отказов в единицу времени,
для простейшего потока
2)поток
восстановлений;
-время
восстановления (величина случайная),
-время
обнаружения отказа,
-время
парирования отказа
Характеризуется
параметром потока восстановления
-
вер-ть того, что процесс восстановления
происходит за время
.
9. Показатели безотказности восстанавливаемых объектов.
Определяются способом задания потока отказов.
а)
задание числа отказов на интервале
времени.
-
вектор числа отказов,w(t)-ведущая
функция потока,
,
-
параметр потокоотказов,
-статистическая
форма, N-число
объектов прошедших испытание,
-
интервал времени,
-
число отказовi-го
объекта на интервале
б) задание закона распределения по времени
f(t) – плотность распределения
-
среднее время работы между отказами.
