
- •Глава 2. Системы линейных уравнений
- •§2.1. Общие понятия системы линейных уравнений
- •§2.2. Нахождение единственного решения системы
- •§ 2.3. Общий подход к решению систем уравнений
- •§ 2.4. Базисные решения системы уравнений
- •§ 2.5. Однородные системы линейных уравнений
- •§ 2.6. Фундаментальные решения системы уравнений
- •§ 2.7. Общее решение системы неоднородных линейных уравнений
- •§ 2.8. Модель Леонтьева многоотраслевой экономики
Глава 2. Системы линейных уравнений
Решение многих экономических задач сводится к исследованию и решению систем линейных уравнений.
§2.1. Общие понятия системы линейных уравнений
Cистема
![]() линейных уравнений с
линейных уравнений с
![]() переменными имеет вид:
переменными имеет вид:
![]() (1)
(1)
или в сокращенной записи
![]() ,
,
![]() .
.
Здесь роль переменных, подлежащих
определению, играют величины
![]() ,
называемые неизвестными. Параметрами
являются переменные
,
называемые неизвестными. Параметрами
являются переменные
![]() и
и
![]() ,
которые могут принимать любые
действительные значения. Все
называются коэффициентами при
переменных, все
- свободными членами уравнений.
,
которые могут принимать любые
действительные значения. Все
называются коэффициентами при
переменных, все
- свободными членами уравнений.
Решением системы называется
упорядоченная совокупность чисел
![]() ,
которая при подстановке в систему
обращает каждое уравнение в тождество.
Линейная система уравнений называется
совместной, если она имеет хотя
бы одно решение, и несовместной,
если она не имеет решений. Совместная
система уравнений называется определенной,
если она имеет единственное решение, и
неопределенной, если она имеет
более одного решения. Две системы
уравнений называются равносильными,
если они имеют одно и то же множество
решений.
,
которая при подстановке в систему
обращает каждое уравнение в тождество.
Линейная система уравнений называется
совместной, если она имеет хотя
бы одно решение, и несовместной,
если она не имеет решений. Совместная
система уравнений называется определенной,
если она имеет единственное решение, и
неопределенной, если она имеет
более одного решения. Две системы
уравнений называются равносильными,
если они имеют одно и то же множество
решений.
Системы уравнений удобно решать в матричной форме. Запишем систему (1) в виде матричного уравнения. Введем обозначения:
 ;
;
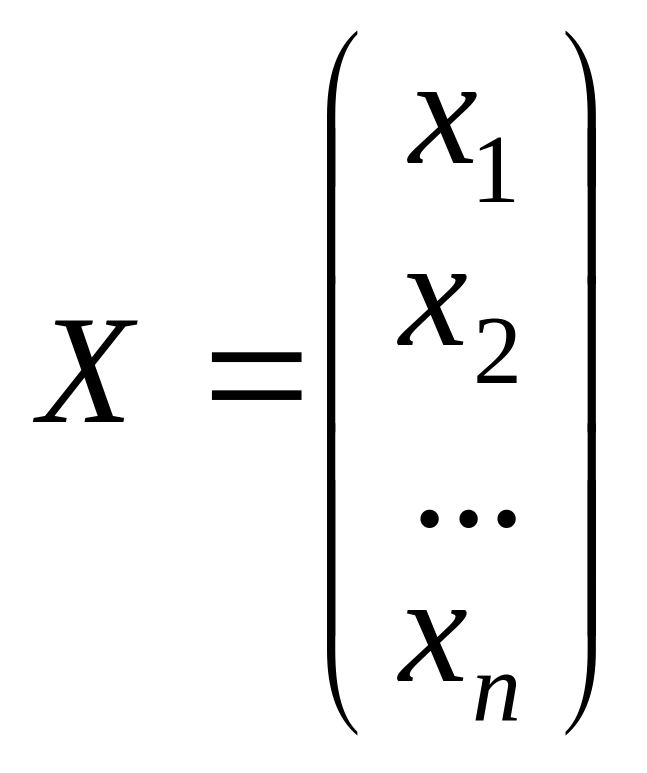 ;
;
 ,
,
где
![]() -
матрица коэффициентов при переменных,
или матрица системы;
-
матрица коэффициентов при переменных,
или матрица системы;
![]() - матрица-столбец неизвестных;
- матрица-столбец неизвестных;
![]() -
матрица-столбец свободных членов. Тогда
система уравнений может быть представлена
в матричном виде
-
матрица-столбец свободных членов. Тогда
система уравнений может быть представлена
в матричном виде
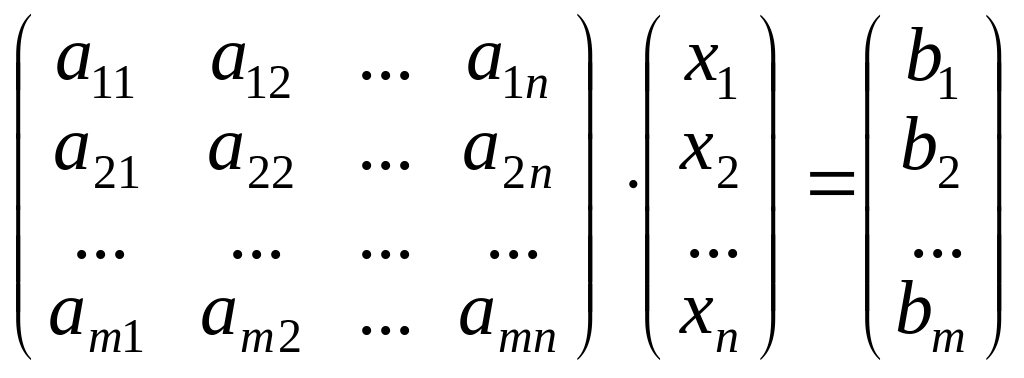
или в компактной матричной форме
![]() .
.
§2.2. Нахождение единственного решения системы
Метод обратной матрицы Метод с использованием расширенной матрицы Метод с использованием формул Крамера |
Рассмотрим вначале частные случаи
решения системы линейных уравнений.
Пусть
![]() и
и
![]() .
.
Метод обратной матрицы
Решим матричное уравнение в случае
и
.
Для матрицы
существует обратная матрица
![]() .
Умножим слева обе части матричного
уравнения на
.
.
Умножим слева обе части матричного
уравнения на
.
![]()
или ![]() .
.
Уравнение в матричном виде решено. Для нахождения элементов матрицы неизвестных следует найти обратную матрицу коэффициентов и умножить ее на столбец свободных членов .
ПРИМЕР. Решить систему уравнений
![]() (2)
(2)
Решение. Напишем систему в матричном виде
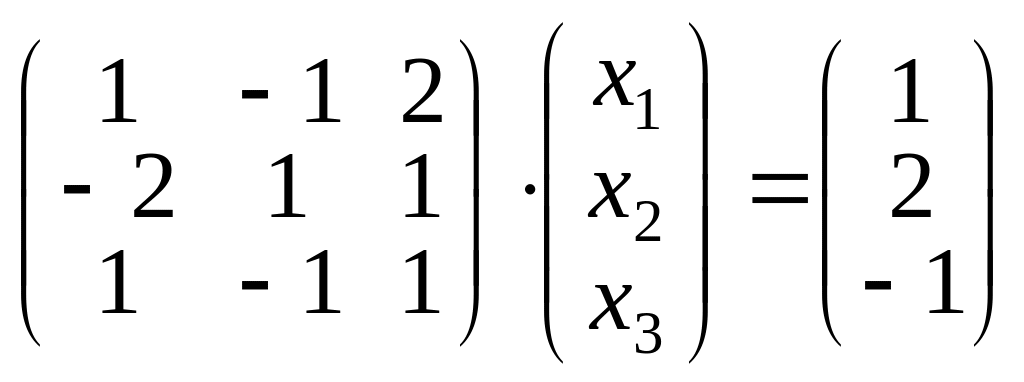 .
.
Матрица коэффициентов

не вырождена (ее
определитель
![]() ).
Поэтому, существует обратная матрица,
которая легко может быть найдена одним
из рассмотренных в главе 1 способов
).
Поэтому, существует обратная матрица,
которая легко может быть найдена одним
из рассмотренных в главе 1 способов
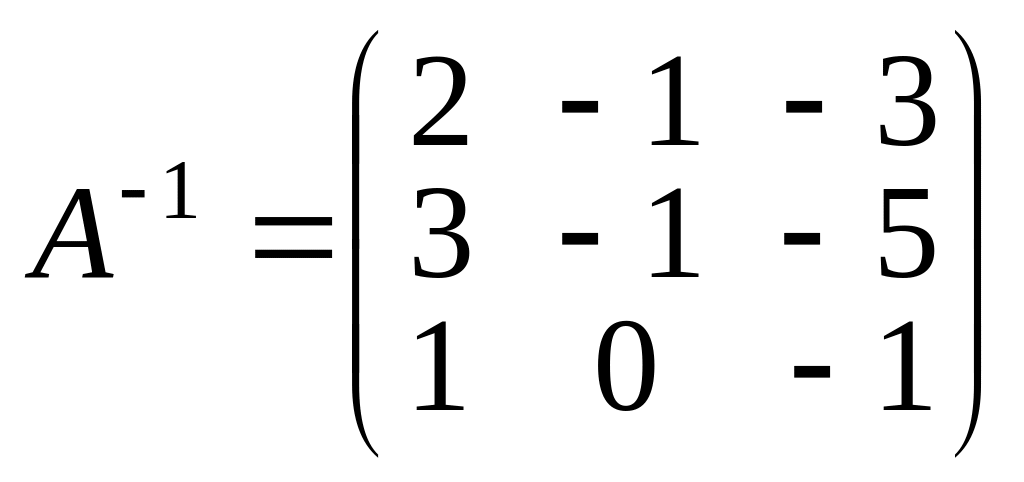 .
.
Находим далее произведение
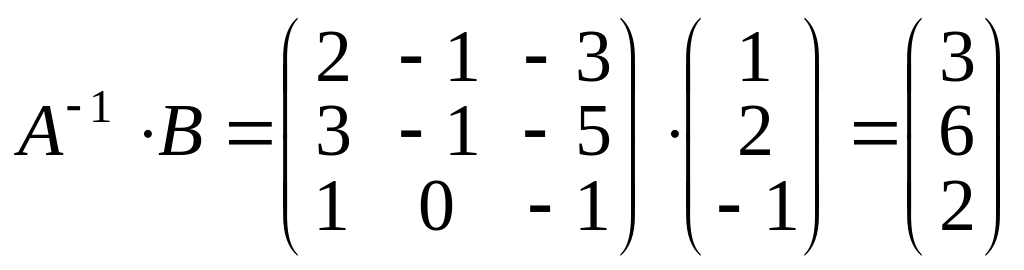 .
.
Матрица неизвестных равна
 .
.
Ответ можно записать
также в виде
![]()
Метод с использованием расширенной матрицы
Более эффективный способ решения системы из уравнений с неизвестными можно осуществить с помощью расширенной матрицы (см. замечание к разделу «Способ построения обратной матрицы», гл.1, § 1.5).
Составим расширенную матрицу
![]() .
.
Элементарными преобразованиями строк расширенной матрицы приведем матрицу к единичной. Тогда матрица обратится в матрицу
![]() .
.
Расширенная матрица примет вид
![]() .
.
Извлекая из расширенной матрицы матричное произведение и приравнивая его матрице неизвестных, получаем для неизвестных равенство
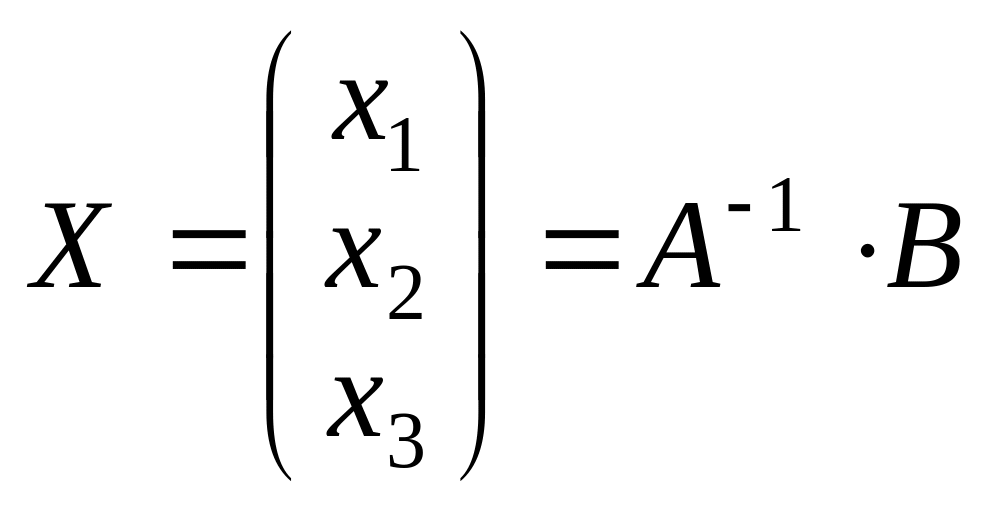 .
.
ПРИМЕР. Решить систему уравнений (2) с помощью расширенной матрицы.
Решение. Составим расширенную матрицу
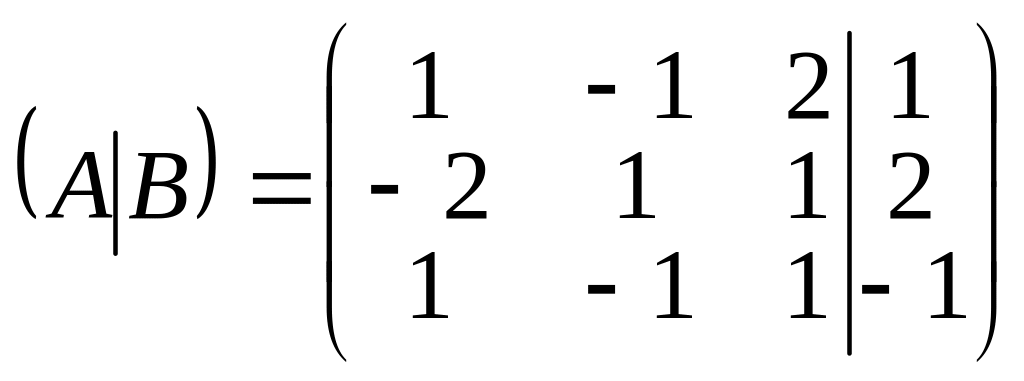 .
.
Приведем вначале матрицу к треугольному виду:
![]()
 .
.
Далее образуем треугольник нулей выше главной диагонали:
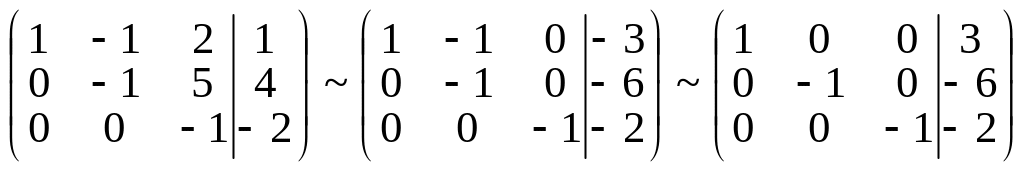 .
.
Наконец, получим единицы на главной диагонали:
 .
.
Следовательно,  .
.
Метод с использованием формул Крамера
Третий способ решения системы из уравнений с неизвестными в случае дает теорема швейцарского математика Габриэля Крамера (1704-1752).
![]()
(о решении системы уравнений с помощью определителей)
Пусть у квадратной
матрицы коэффициентов при неизвестных
в системе из
линейных уравнений с
неизвестными определитель
.
Пусть
![]() -
определитель матрицы, получаемой из
матрицы
заменой
-
определитель матрицы, получаемой из
матрицы
заменой
![]() -го
столбца столбцом свободных членов.
Тогда система имеет единственное
решение, имеющее вид
-го
столбца столбцом свободных членов.
Тогда система имеет единственное
решение, имеющее вид
![]() .
.
◄Развернем матричное уравнение и запишем обратную матрицу через алгебраические дополнения:
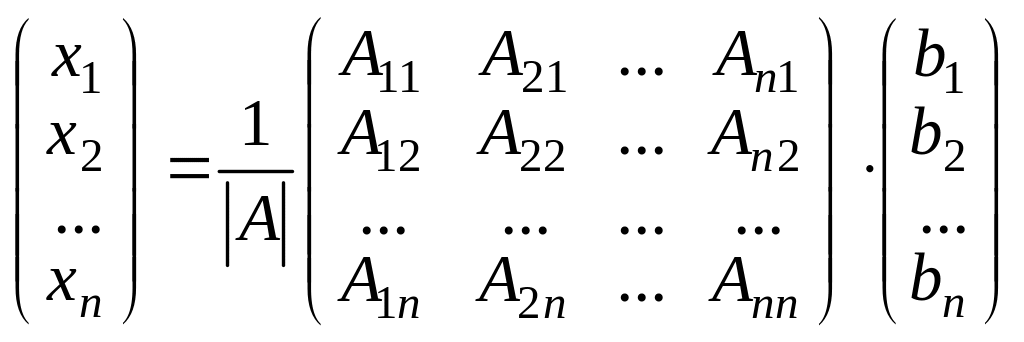 .
.
Перемножив матрицы, получим
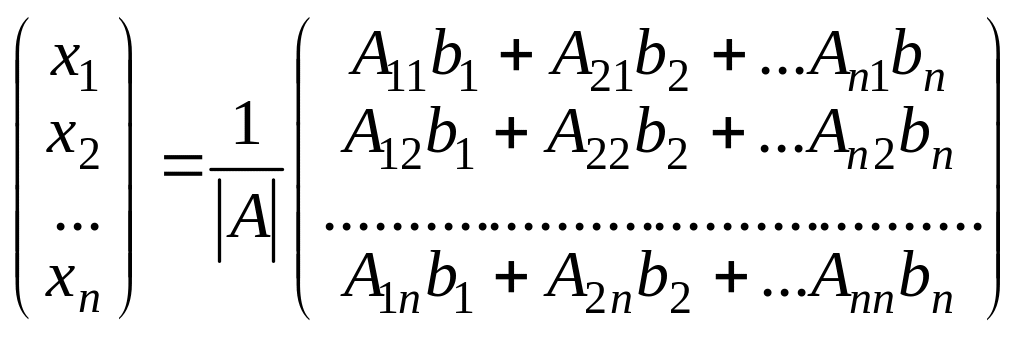 .
.
Сумма
![]() представляет собой произведение чисел
представляет собой произведение чисел
![]() на алгебраические дополнения элементов
1-го столбца. Она равна определителю
матрицы, полученной из данной заменой
элементов этого столбца на числа
(свойство 9 определителей). Следовательно,
на алгебраические дополнения элементов
1-го столбца. Она равна определителю
матрицы, полученной из данной заменой
элементов этого столбца на числа
(свойство 9 определителей). Следовательно,
 .
.
Аналогично сумма
![]() есть произведение чисел
на алгебраические дополнения элементов
2-го столбца. Тогда
есть произведение чисел
на алгебраические дополнения элементов
2-го столбца. Тогда
 .
.
Продолжив вычисления, окончательно получим
.►
Способ решения системы линейных уравнений, основанный на формулах Крамера, получил название метода или правила Крамера.
ПРИМЕР. Решить систему уравнений (2) методом Крамера.
Решение. Условия,
при которых правило Крамера работает
(![]() )
выполнены. Воспользуемся формулами
Крамера
)
выполнены. Воспользуемся формулами
Крамера
 ;
;
 ;
;
 .
.
Замечание. Перечисленные методы решения
систем линейных уравнений становятся
трудоемкими при ручном счете уже при
![]() .
Однако они удобны при решении задач
на компьютере.
.
Однако они удобны при решении задач
на компьютере.
Рассмотренные методы являются решением систем частного вида, для которых выполняются условия . Перейдем к рассмотрению решения линейных систем общего вида. В дальнейшем будем оперировать понятиями матричной алгебры.
