Н

Называется индексной строкой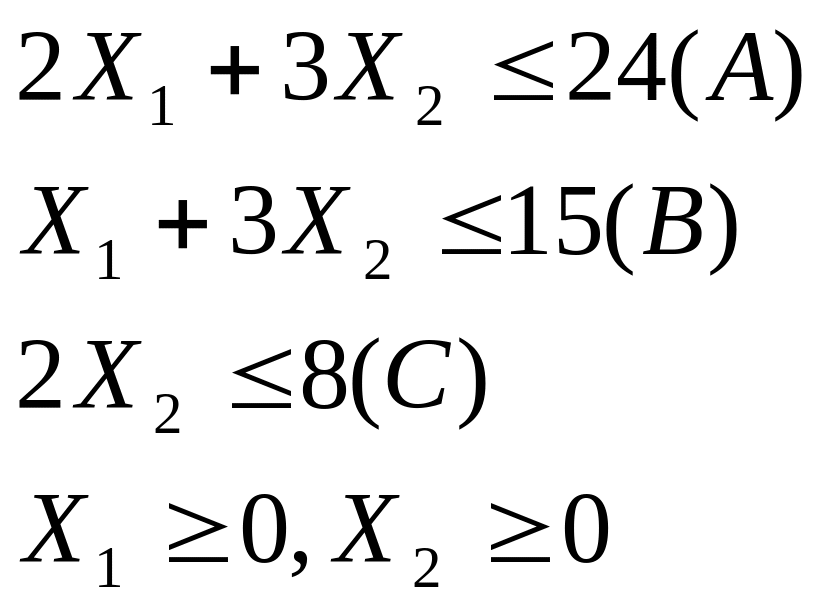

Текущее решение

ижние строки определяют разницу между

Алгоритм определения оптимального решения:

исходя из выше изложенной теории данные, полученные в симплексной таблице или в таблице вообще при максимизации целевой функции, решение будет оптимальным, если в индексной строке не будет отрицательных чисел

при минимизации целевой функции, решение будет оптимальным, если в индексной строке не будет положительных чисел ( это так называемая двойственная задача линейного программирования)

Правила составления 1-ой итерационной таблицы по отправной

1. наибольшая по абсолютным значениям переменная, в индексной строке отправной таблице, указывает на новую базисную переменную, подлежащую замене

2. определение старой базисной переменной, которая должна в новом решении уступить место новой базисной величине, выбирается путем деления свободных членов столбца В на Х2

24/3=8,

15/3=5,

8/2=4.

Найденные отношения определяют переменные старого значения, которые должны уступить место новой переменной, оно должно быть минимальным, т.е. Х2 заменяется на Х5

Столбец новой базисной переменной называется ключевым столбцом. Строка, куда попадают новые переменные, называется ключевой строкой.

На пересечении ключевой строки и ключевого столбца стоит генеральный элемент.

Составляем i=2 симплексную таблицу:

С/б	Х/б	В	1	2	0	0	0
			Х1	Х2	Х3	Х4	Х5
0	X3	12	2	0	1	0	-3/2
0	X4	3	1	0	0	1	-3/2
2	X2	4	0	1	0	0	½
Zj-Cj		Z=8	-1	0	0	0	1

Правила составления i-ой текущей итерационной таблицы: i = (1,n)

1. старый ключевой столбец переписывают в новую таблицу в виде нулей кроме элементов стоящих на перемещении столбца и ключевой строки

2. элементы новой строки соответствуют старой ключевой строки, она находится путем деления

элементов старой ключевой строки на генеральный элемент.

при формировании базисной строки вместо Х5--------Х2

3. столбцы старой таблицы, содержащие в ключевой строке «0», переписываются в новую таблицу без изменения

4. все остальные элементы новой таблицы определяются по формуле:

новый = старый (минус) элемент ключ строки * элемент ключ столбца

лемент элемент генеральный элемент

пример

24 - 8*3/2=12

15 - 8*3/2=3

0 - 1*3/2=-3/2

Решение не оптимально (8 рублей прибыли на ед. продукции), т.к. имеется в индексной строке отрицательное значение. По второй итерации выпуск продукции 2 вида в количестве 4 ед. за час, при этом, предыдущий получает прибыль 8 рублей в час, и остаются, не использованы машины в цехе

А-12шт, в цехе В-3 шт.

Используя выше изложенные правила, проводим следующее итерационное решение. Составляем новую таблицу, выделив в таблице 2 ключевой столбец и ключевую строку, получив генеральный элемент на их пересечении. Пользуясь правилами, заполняем таблицу i= 3:

С/б	Х/б	В	1	2	0	0	0
			Х1	Х2	Х3	Х4	Х5
0	Х3	6	0	0	1	-2	3/2
1	Х1	3	1	0	0	1	-3/2
0	Х2	4	0	1	0	0	1/2
Zj-Cj		Z0=11	0	0	0	0	-1/2

12-3*2/1=6

4-0*3/1=4

0-1*2/1=-2

-3/2-(-3/2*2)/1=3/2

т.к. в индексной строке имеется отрицательное значение, то решение не является оптимальным и целевая функция не отражает максимум прибыли (11 рублей). Введем еще одну итерацию В таблице 3 определяем ключевую строку и ключевой столбец и, используя правила1-4., составляем i=4 таблицу.

С/б	Х/б	В	1	2	0	0	0
			Х1	Х2	Х3	Х4	Х5
0	Х5	4	0	0	2/3	-4/3	1
1	Х1	9	1	0	1	-1	0
2	Х2	2	0	1	-1/3	2/3	0
Zj-Cj		Z0=13	0	0	1/3	1/3	0

В индексной строке отсутствуют отрицательные значения, следовательно это и есть оптимальное решение, максимум прибыли составляет 13 рублей.

“Двойственная задача в линейном программировании.”

На практике часто приходится сталкиваться с задачами планирования при условии минимизации целевой функции. Такого рода задачи обычно связаны не с получением максимальных доходов или прибыли, а с получением минимальных затрат, необходимых для решения производственных задач, приносящих максимальную прибыль.

В качестве примера рассмотрим первую задачу оптимизации плана производства, в которой выпускается 2 вида продукции в цехах А, Б и В, оснащенных оборудованием в следующих количествах:

	1	2
А	2	3
Б	1	3
В	-	2

- объем выпуска продукции первого и второго вида соответственно.

(прибыль)

шт/час шт/час р/час

Примечание:

В двойственной задаче, если ограничения имеют знак ≥, то для выравнивания левой и правой части ограничения, вводится базисная переменная со знаком “+”, если ограничения имеют знак ≤, то вводится базисная переменная со знаком “-“, например:

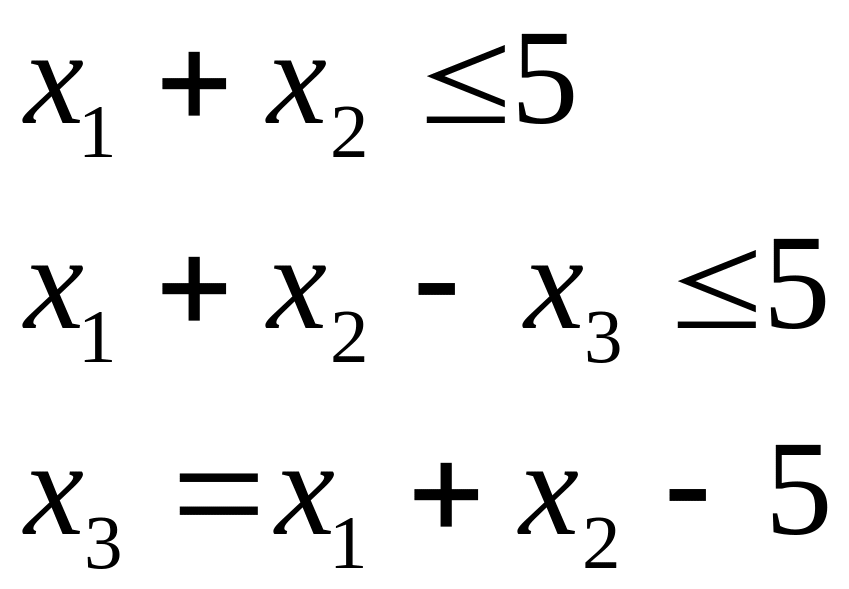
Примечание:

Если “5” – минимально допустимый результат, то - величина превышения этого результата.

Если независимые переменные вводятся со знаком “+”, то они показывают количество неиспользуемых ресурсов (см. лекцию 10).

Если базисная переменная вводится со знаком “-“, то она показывает избыток продукции при постоянстве ресурсов.

Применительно к 1-ой задаче, в рамках её двойственности, можно потребовать рассмотрение задачи аренды оборудования, необходимого для выпуска продукции и минимизировать общую плату за арендное оборудование. В этом случае формализация задачи минимизации арендной платы оборудования при производстве продукции вида будет иметь вид:

Пусть - аренда 2-х маш/час на ед. продукции вида 1 оборудования цеха А.

В цехе А – 24 станка.

- арендная плата за 1 час использования станка цеха Б.

- арендная плата за 1 час использования станка цеха В.

При выпуске единицы продукции первого вида, по условию задачи из таблички надо использовать 2 маш/часа оборудования цеха А и одного машиночаса оборудования цеха Б, при этом получается прибыль при производстве 1-го вида продукции – 1 руб. Для второго

вида продукции, по аналогии, прибыль – 2 руб. Требуется минимизировать арендную плату за оборудование при производстве 2-х видов продукции.

При введенных обозначениях имеем:

(плата за аренду должна быть менее 1 руб.)

Выбор оптимальных вариантов решения:

1. Приводим систему уравнения к канонической форме:

Сведем решение к симплексному методу:

Сб	Уб	В	24	15	8	0	0	М	М
			y1	y2	y3	y4	y5	y6	y7
М	y6	1	2	1	0	-1	0	1	0
М	y7	2	3	3	2	0	-1	0	1
Zj-Cj		3M	5M-24	4M-15	2M-8	-M	-M	0	0

Переход от отправной таблицы к следующей производится в соответствии с правилами симплексного метода (лекция 10).

В соответствии с чем, ключевым столбцом будет 4-ый, ключевой строкой будет 1-ая, на их пересечении – генеральный элемент.

Используя 4 правила из лекции 10, составим 2-ую таблицу:

Сб	Уб	В	24	15	8	0	0	М	М
			y1	y2	y3	y4	y5	y6	y7
М	y1	0,5	1	0,5	0	-0,5	0	0,5	0
М	y7	0,5	0	1,5	2	1,5	-1	-1,5	1
Zj-Cj		0,5M-12	0	1,5M-3	2M-8	1,5M-12	-M	-2,5М+12	0

Примечание:

В двойственной задаче, коэффициент при базисной переменной принимается, как большое число, условно равное М, превышающее по своему значению максимальный коэффициент при независимой переменной целевой функции.

Дальнейшие итерационные процедуры проводятся до исчезновения в индексной строке положительных чисел, оптимальным для ЛПР будут значения затрат по арендной плате без наличия в индексной строке отрицательных чисел.

Линейное программирование методом потенциалов в транспортных задачах.

В транспортных задачах обычно имеется база А располагающих каким-либо количеством машин n и объекты (потребители) Б нуждающихся в этих машинах, количество потребляемых машин объектами Б (m).

Машины объектам Б нужны для выполнения запланированного объема работ.

База А и объекты Б заинтересованы в обеспечении min простоя машин которые зависят от плана распределения их по базам и объектам. В ЛП потенциалами являются некоторые числа U_Ai и U_Бj соответственно к базам и объектам. Сумма которых для клеток табличного плана содержащих цифры распределенных машин, применяется равным результатов времени простоев:

U_Аi+U_Бj=C_ij (12.1)

Там где в клетках табличного плана нет распределения машин по объектам эта сумма будет не более стоимости результатов (Cij*Хij)

UАi+UБj (Cij*Хij) (12.2)

План распределения машин по объектам отображенный в таблице планов все клетки которого отвечают условиям 12.1, 12.2 являются оптимальными.

Задача: транспортная и РУР для ее решения.

Описание реального объекта.

Пусть имеются предприятия занимающихся механизацией трудоемких работ и располагает набором однородных технических средств в количестве n=30 еденицам. Машины размещаются на 3х базах Реутово (А1), Железнодорожный, (А2) Балашиха, (А3) при этом базы А1и А2 имеют по 11 машин, а база А3 8ед. Использование этой техники планируется на 4х объектах Б1,Б2,Б3,Б4.

Объекты Б1 нуждаются в 5ед.

Б2 и Б3 нуждаются в 9ед.

Б4 нуждается в 7ед.

Эффективность эксплуатации max средств во многом зависит от того на сколько интенсивно они используются или не используются простаивают. При этом чем меньше время простоев, тем выше эффективность технических средств.

Под простоем здесь понимается количество свободного времени (Тij) в течение которого ТС базой Аi не используются объектом Бj. Общая характеристика использования ТС с указанием ее наличия и потребности на объектах и базах приведено в таблице 12.1

таблице 12.1

Базы	Кол-во ТС	Объекты				UАi
		Б1 5	Б2 9	Б3 9	Б4 7
А1	11	7	8	5	3
А2	11	2	4	5	9
А3	8	6	3	1	2
Uвj

Требуется разработать такой план распределения ТС по объектам, при котором суммарное время простоев ТС будет минимальным.

Последовательность действий выбора наилучшей альтернативы методом потенциалов.

* составляем исходный план распределения машин по следующим правилам:

а) в правом верхнем углу клеток таблицы поместим цифры простоев ТС, а в левые нижние углы тех же клеток цифры характеризующие количество распределяемых единиц ТС.

б) в нижнюю строку исходной отправной таб. Вводится потенциал UВj, а в правый крайний столбец вводится потенциал UАi.

* правило заполнения строк:

таблице 12.2

Базы	Кол-во ТС	Объекты				UАi
		Б1 5	Б2 9(3)	Б3 9(5)	Б4 7
А1	11 (4)	5 < 7	7<8	5 4	3 7	0
А2	11(6)	2 5	4 6	2<5	0<9	-3
А3	8 (3)	1<6	3 3	1 5	-1<2	-4
Uвj		5	7	5	3

а) при заполнение первой строки выбираем направление то, время простоя минимально, т.е А1и Б4, здесь время простоев имеет стоимость С1 4=3. Количество машин на этом направлении устанавливаются как минимальный из их общего количества имеющая на А1 и потребного для Б4=7ед. При таком распределении достигается либо полный расход ТС , данной базы, либо полное насыщение данного объекта. В данной задачи полностью насыщается объект Б4. На базе А1 остается 4ед.

б) остаток ТС на базе А1 целесообразно направить на объект Б3 и по первому плану составляет количество простоев.

в) т.к все ресурсы А1 исчерпаны, а в направлении А1 Б3 остаются потребности в 5ед.

Используя правила выше изложенные заполним строки в направлении А2 иА3.

В результате получаем первый исходный план распределения машин по объектам .

Проверяем теперь соблюдение условий потенциалов для свободны клеток с этой целью просуммируем для каждой из них соотношения потенциалы баз и объектов и сравним их значения с временем простоев проставленных в таб. 12.1.

Проверка соблюдений условий потенциалов для свободных клеток

UБ3=С13-UА1=5-0=5

UБ4=С14-UА1=3-0=3

UА3=С33-UБ3=1-5=-4

UБ2=С23-UА3=3-(-4)=7

UА2=С22-UБ2=4-7=-3

UБ1=С21-UА2=2-(-3)=5

Сравним значения суммы потенциалов баз UАi и UБj с временем простоя таблицы 12.1

UА1+UБ1 5+1 7

UА1+UБ2 7+0 8

UА3+UБ1 -4+5 6

UА2+UБ3 -3+5 5

UА2+UБ4 3-3 9

UА3+UБ4 -4+3=-1 2

Этот план транспортировки распределения средств по объектам и базам является оптимальным , в случаи если хотя бы в одной из клеток нарушены условия по стоимостям простоя, то план подлежит улучшению путеи перехода к следующей итерациональной процедуре.

Резюме:

Из изложенного видно, что оптимизация плана распределения ТС в процессе РУР для транспортной задачи по критерию min простоя сводится в 4 этапа:

1 этап Составление описание задачи и отправной таблицы по строкам.

2 этап Расчет потенциалов

3 этап Расчет псевдо стоимости

4 этап Проверка оптимальности переход к улучшению плана в случаи нарушения условий хотя бы в одной клетке.

Линейное программирование методом приращения в задачах

распределения инвестиций.

Этот класс задач возникает в рыночных отношениях в случае наличия одного или нескольких инвесторов, располагающих свободным капиталом и желающих получить после его вложения прибыль с заданным уровнем потерь в условиях ограничений.

В методе приращения ЦФ L(х)=С1Х1+С2Х2+….+СnХn рассматривается при следующих ограничения

L1 х1 1

. 13.2

.

Ln хn n

Суммарный эффект в этом методе определяется в виде

Э=[1-(-1-Р1) ^х1-2.1]+….+[1-(1-Рn)^хn-Ln]= [1-(1-Рi)^хi-Li] 13.3

Где в выражения 13.2 и 13.3 введены следующие обозначения

Хi- объем инвестиций итого инвестора

Li, i- нижние и верхние значения объема соответственно

Рi-исходная вероятность получения прибыли

Э-суммарный эффект доставляющий минимальные потери, целевой функции 13.1 алгоритм РУР.

1.В качестве исходного состояния значения параметра х0 берутся их минимальные значения L1….Li….Ln

2.На первом шаге итерации из аргументов х0 дается определенное приращение хi0, вытекающий из условий 13.3 полученные в результате значения переменных образует «чистый набор» для хi равный

хi=хi1;хi2

3.Из х0 и х1 составляют два первых, комбинированных состояний, в каждом из которых один из аргументов соотношение новому значению.

4.На 2м шаге с помощью приращений наращивания значения аргументов исходя из «комбинированных состояний»исходя из ограничений 13.2 в итоге снова получаются «чистые и комбинированные» состояния далее итерация продолжается по изложенному пункту 5ь

5.На каждом шаге для «чистых и комбинированных» сост. неременных вычисляются значения L(х) 13.1,min значение Lк(х) на к-м шаге по всем чистым стратегиям данного и пришедствующих шагов обозначаются Lк(х), а по всему комбинированных сост. через Lк(х).

Итерационный процесс min потерь от инвестиций будет продолжаться до тех пор пока не будет выполняться условие достижения заданного уровня теперь Е.

Примечание:

В выражение 13.4 Е явл. требования точности решение задач (оценкой потерь которая задается инвесторам ) на основе располагаемой им статистики.

Задача: Распределение инвестиций

Пусть 2а партнера по бизнесу решили вложить капиталя в одно предприятие на основе предшествующего опыта. Можно определить вероятность успеха партнеров Р1=0,5, Р2=0,3, а также о величине их возможных финансовых потерь С1=0,8, С2=0,4.

Известны приделы капитальных вложений . Min капитальных вложений 1го партнера L1=1 2го L2=7. Max капитальных вложений 1го 1=2 2го =10.

Задана также требуемая эффективность решаемых задач. Э=0,9.

Эффективность рассматривается как вероятность заданная.

Требуется найти объемы Х1opt и Х2opt оптимальных вложений обоих партнеров обеспечивающих:

Заданную вероятность успеха

Обращ. в min потери партнеров ЦФ L(х)=С1Х1+С2Х2, при в веденных ограничениях на эти объемы.

Решения

Сост. исходное сост. аргументов

Х0=(Х01,Х02) или =(L1 L2)=(1,7)

Рассчитывается приращение Х которые обратно пропорциональным потерям

Х01=1/С1=1/0,8=1,25t

Х02=1/C2=1/0,4=25t 13.5

Для расчета величины t воспользуемся требованиями Э=0,9, а поскольку это вероятность успеха, то из теории вероятности известно, что вероятность не успеха операции «инвестиция», при 2х «зависимых» партнера имеет вид:

Э=0,9=1-[(1-Р1)^х1-L1(1-Р2)^х2L2] 13.6

В соответствии с правилами этого метода параметр t из 13.5 определяется из граничного условия z=0, при этом соотв. показательной степени в 13.7 принимают значения Х01 и Х02.

Z=0,1-0,5^1,250,7-0^2,5t 13.8

Из 13.8 следует, что t=1,21 тогда с учетом 13.5 Х01=1,25=1,25 1,21=1,51

Х02=2,5t=2,5 1,21=3,02

Выполняется 1й шаг интеграции. Чистое состояние.

Х11=L1+ Х01=1+1,51=2,51

12=L2= Х02=7+3,02=10,02

Х1=(Х01;Х02)=(2,51,10,02)

Комбинированное состояние

Х1=(10,02,10) (2,51,2)

По 13.1 рассчитывает значение L1(Х), при чем из 2х последних знаний для чистого состояния выбирается минимальное.

L1(х1)=(0,8 2,51+0,4 0,4 10.02)=6,016 чистое состояние

Для комбинированных состояний

L1(Х)=0,8 1+0,4 10,02=4,808

L1(Х)=0,8 2,51+0,4 2=2,808

Min 2,808=L1(Х).

Из требуемой гарантированной вероятности успеха Э=0,9 следует что Е=0,1,тогда L(Х)-L(Х) 0,1

6,016-2,808=3

Решение на первом шаге не соответствует принятой точности Е в оценке потерь, т.к оно взято из чистого состояния и составляет 2,51 и 10,02, поэтому осуществляется второй шаг итерации и состаляются используется те же правила и тот же алгоритм, но уже получаются 2 чистых состояния и 4 комбинированных. В соответствии с пунктом 4е алгоритма по выражению 13.1 рассчитываются:

L1(Х)=min из 2х чистых состояний

L2(Х)=min из 4х комбинированных

На втором шаге пункте 5ь алгоритма определить разность L2(Х)-(Х) Е между min чистыми и min комбинируемым состоянием, если эта разность превышает уровень заданных потерь Е, то переходят к 3ей итерационной процедуре.

Лекция 15. Динамическое программирование в задачах

распределения однонородных ресурсов.

Впервые, такого класса задачи были решены методом динамического программирования применительно к военным целям. Метод специально разрабатывался для распределения определенного количества однотипного оружия, по однотипным или разнотипным целям.

Алгоритм метода динамического программирования был перенесен с задач военного характера на задачи, которые стоят перед менеджером распределяющего финансовые ресурсы по исполнителям.

Все действия которые менеджер совершает в процессе распределения однородного ресурса, это многоэтапный процесс, протекающий во времени.

Алгоритм динамического программирования включают следующие этапы:

Общий этап

Имеется некая управляющая операция (распределение финансов генеральным директором) распадающаяся (естественно или искусственно) на m шагов.

На каждом шаге осуществляется распределение и перераспределение ресурсов участвующих в операции с целью улучшения ее результатов в целом. Эти распределения ресурсов в МДП (метод динамического программирования) называются управлениями U-операциями.

Эффективность операций в целом (приращение денег в банке) оценивается тем же показателем что и показатель эффективности управления. При этом Э(U) зависит от всей эффективности управления на каждом шаге операций. Тогда Э =Э(U)=Э(U1,U2….Un).

Управление при каждом показатель Э достигается max называется оптимальным управлении Uopt

Задачи динамического программирования заключаются в том, чтобы определить на каждом шаге Uiopt, где i=(1,m) и тем самым оптимальное управление в целом.

В большинстве задач МДП

Э = Эj max, где Эj-эффективность операций на этом шаге.

Динамическое программирование при решение задач распределения ресурсов осуществляется в два круга. В начале от последнего шага к первому. Затем в обратном направлении от первого к последнему.

На первом круге (от последнего шага к первому) находится условно-оптимальное управлении.

Оно выбирается таким чтобы все предыдущие обеспечивали max Эi+1го шага. Иначе на каждом шаге имеется такое управление Ui которое обеспечивает оптимальное продолжение операции при Эi-1 или Эi+1.Этот принцип выбора управления называется принципом оптимальности Беллмана. Так продолжается до первого шага.

Поскольку первый шаг имеет предыдущего, то полученные для него условное Uopt терпит свой условный характер и становится просто оптимальным управлением, играющий роль исходного для второго круга.

Второй круг оптимизации начинается с первого шага для каждого оптимального управления U1opt известно, имея все шаги после него устанавливают Uiopt оптимальное управление становится понятным или известен алгоритм действий который при его реализации на 2м круге обеспечит оптимальность всей операции в целом. На практике встречается много задач по распределению однородных ресурсов решаемых МДП, одно наиболее часто к этому методу приходится прибегать в задачах распределения однородных ресурсов.

Обычно в задачах распределения однородных ресурсов имеет место много этапность процессов, протекающих во времени.

В методе динамического программирования имеется некоторая управляемая операция (процесс - объект), распадающаяся на m-этапов. На каждом этапе осуществляется распределение n- нераспределенных ресурсов, участвующих в операции с целью улучшения ее результатов в целом.

Эти распределения ресурсов в динамическом программировании называются управлением операцией (процесс преобразования управляющего ресурса в управляющее воздействие).

Эффективность операции в целом оценивается тем же показателем, что и эффективность ее управления.

При этом Э(U) зависит от всей совокупности управлений на каждом этапе операции:

Закон управления, при котором показатель достигает max, называется оптимальным управлением ( ).

Задача динамического программирования всегда требует определить оптимальное управление на каждом этапе , i = (1,m) и тем самым оптимальное управление в целом.

В большинстве задач, в том числе и задач распределения ресурсов требуется обеспечить:

, где - эффективность операции на i- этапе процесса (операции).

Все вышеизложенное является постановкой задач динамического программирования в общем виде.

Примечание:

задача ДП как и другие задачи управления решается при наличии управленческого ресурса.

Решение задач ДП заключается в следующем алгоритме: оптимизация методом последовательных приближений, итераций в задачах ДП производится в 2 круга: в начале от последнего этапа к первому производится распределение начального ресурса от последнего этапа к первому, а затем в обратном направлении от первого к последнему.

На первом круге от последнего этапа к первому находятся т.н. псевдо оптимальное управление (иногда условно оптимальное). Оно выбирается таким, чтобы все предыдущие этапы обеспечивали этапа.

В общем, на каждом этапе имеется такое управление , которое обеспечивает псевдо оптимальное продолжение операции на этапе, этот принцип выбора управления называется принципом оптимальности Беллмана.

Так продолжается до первого этапа, но поскольку перед первым этапом нет предыдущего, то полученное от него псевдо оптимальное управление теряет свой псевдохарактер и становится просто начальным управлением, которое должно быть переведено в оптимальное.

Второй круг оптимизации начинается с первого этапа, для которого псевдо оптимальное управление, полученное на первом круге, переводится в путем вычитания из

(псевдо оптимум), (15.1)

где - разница между начальным значением ресурса на начало года и конечным значением ресурса на конец года.

Имея для всех этапов псевдо оптимальное управление и значения на конец каждого этапа накопленного ресурса (14.1) будем иметь оптимальное управление на каждом этапе второго

круга. На этом первая итерация заканчивается. Итерационные процедуры продолжаются до тех пор, пока не будет достигнуто начальное значение начального ресурса, характеризующего возможности субъекта, проводящего операции.

Рассмотрим алгоритм ДП при решении задачи распределения однородного ресурса, имеющей следующие

исходные данные:

Фирма планирует совместную работу сталелитейного и автомобилестроительного заводов на трехлетний период. Начальный запас стали составляет 2300т., начальные мощности 1200т. стали и 200шт. автомобилей в год. Сталь (сырье) расходуется на производство автомобилей в количестве 4т. на 1 автомобиль на автозаводе, а на производство собственной стали на литейном заводе в соотношении 1т. затрат на 4т. выпуска.

Кроме того сталь расходуется на увеличение мощности автозавода в соотношении 10т. затрат, прирост мощности 1 авто в год и на увеличение мощности сталезавода в соотношении 1т. затрат, прирост мощности сталезавода 0,15т. в год.

Решение о распределении стали на следующий год принимается по показателям очередного года.

Требуется определить мах объем выпуска продукции (авто) за весь планируемый период.

Решение сводится к построению процесса распределения начального запаса стали т. по трем потребителям: автозавод на развитие, сталезавод на развитие, сталезавод на собственное производство в течение трех плановых лет. Процесс максимизации выпуска авто складывается из следующих этапов, последовательно протекающих во времени и отражающих реальный процесс.

Этап 1: на сталезаводе

Планирование выпуска объема стали, необходимого для производства авто на автозаводе, исходя из начальной собственной мощности при наличии начального запаса =1200т. , шт.

Этап2: планирование выпуска объема стали на собственное производство определяется коэффициентом пропорциональности равным 1т. затрат на 4т. выпуска = 0,25

Этап3: планирование выпуска объема стали на увеличение мощности сталезавода

= 0,15т. к 1т. затрат.

На автозаводе:планирование выпуска авто, исходя из начальной мощности завода .

Планирование выпуска объема авто с учетом мощности ее развития.

= 4т./10т. затрат = 0,4

Согласно методу динамического программирования применительно к нашей задаче имеем 3 управления: в каждом плановом периоде соответственно.

На основании вышеизложенного алгоритма составляем исходную таблицу:

	Развитие автозавода =0,4	Развитие сталезавода =0,15	Собственное развитие сталезавода =0,25
1	200(1+0,4) = 280	1200*1,15 =1380	4*280*1,25 =1400
2	280(1+0,4) =392	1380*1,15 =1587	4*392*1,25 =1960
3	392(1+0,4) =548	1587*1,15 =1825	4*548*1,25 =2740

1220 4792 6100

Определить псевдооптимальное управление первого круга, начиная с третьего периода.

Здесь наша задача заключается в том, чтобы найти количество стали необходимое для выпуска авто в каждом периоде.

На втором плановом периоде:

На первом плановом периоде:

На втором круге оптимизации при определении оптимального управлений и при переходе к ним от псевдооптимальных имеем =850т.

Нам необходимо для производства 280 авто на начало планового периода 850т. стали, а на конец планового периода в соответствии с количеством стали на сталезаводе, выпущенной для развития, в соответствии формулой (14.1) будем иметь оптимальное значение

Определяем оптимальное управление на конец второго периода:

На конец третьего периода:

-355 / 4 = 89 максимально возможный выпуск авто при таком начальном запасе без пересмотра коэффициентов и без пересмотра итерационной процедуры :280+392+548-89 =1131 авто.

Если такой план выпуска авто при таком начальном ресурсе не устраивает менеджера, у него есть инструмент, который позволит ему сменить с 0,4 до цифры другой итерационной процедуры.

Задача: Распределение однородных ресурсов

Пусть имеются 5 видов ресурсов m=5, предназначенных для 4х объектов (этапа производственного плана) n=4. Из предыдущей практики было известно характеристики объектов и ресурсов: материальный эффект, при распределении на j объект любой единицы ресурсов Аi. Коэффициент Li характеризует возможности каждого из ресурсов применительно к конкретному объекту.

Характеристики заданы в таблице 14.1.

Хар-ка ресурсов	1	2	3	4
Ai	16	14	12	2
Li	0,1	0,1	0,1	0,1

Требуется определить количество единиц ресурса Х использование которых на каждом из объектов обеспечит максимальный эффект.

Решение:

В данной задаче нет естественного разделения операций на шаги. Такое разделение введем искусственно в соответствии с требованиями 1го пункта алгоритма. За шаги последовательное распределение ресурсов по объекту n=4.

На первом шаге обозначим Х1-количество ресурсов направляемых на 4-й объект, счет шагов с конца. При этом расчет эффективности этого решения, в силу специфических особенностей задачи планирования производства, произведенных по выражению.

Э1=f1(x1)=A4Pi=A4(1-e^-L4X1)=2(1-е^-0,1х1) 15.2

где Рi=1-е^{-Li х1}

В выражении 14.1 значение х1, известно т.к это количество ресурсов, которое осталось от условного оптимального U управлении на предпоследних от конца (2м от конца шаге).

Переберем все возможные значения х1 и для каждого из них рассчитываем f1(х1) или Эi.

Как видно из условий задачи х1 может принимать значения m=0,1,2,3,4,5. Подставляем в 14.1 значения m и после расчетов получаем:

Х1	f1(Х1)
0	0
1	0,19
2	0,363
3	0,518
4	0,659
5	0,787

На втором шаге (с конца) выделяется Х2 ресурсов, а соответственно Э2=f2(х2) должно учитывается по мимо эффекта от второго шага также эффект в результате условно – оптимального управления на первом с конца шага, тогда;

Э2=f2(X2)=Аn-1[1-е^-Ln-1(x1-x2)] 15.3

Max – ый эффект получаемый за 2 шага получается по формуле. Подставляя значения A3 и L3 в 14.2 и проведем расчеты для распределения ресурсов на втором шаге.

Таблица 14.3

Х2	f2(Х2)	Х1(Х2)
0	0	0
1	1,15	0
2	2,175	0
3	3,108	0
4	3,954	0
5	4,722	0

В таб. 14.3, по формуле 14.2 проведены расчеты всех возможных расчетов Х2. Эффективности и одновременно определены значения Х2 зависящие от Х1 при котором f2(х2) достигает max.

Далее аналогично определяем для всех возможных Х3 значения f3(Х3) и Х3(Х2).

Таб 14.4

Х3	f3(X3)	Х3(Х2)
0	0	0
1	1,33	0
2	2,541	0
3	3,508	2
4	4,68	2
5	5,804	2

Э3=f3(Х3)=А2(1-е^{-L2{x3-f2(x2)}})

Аналогичным путем рассчитываются условно – оптимальное на 4ом шаге с конца на первом с начала, но на этом шаге имеется исходная начальная единица ресурсов предназначена для всех этапов, то начинается 2 й круг оптимизации в обратном порядке.

По сколькую в начале для всех объектов имеются 5 единиц ресурсов m=5, а после выделения ресурсов на один из объектов в соответствии с условно – оптимальным управление Х3(Х2)=2, то тогда Х4(Х3)=3

Х4=U4=5ед-2ед=3ед.

Оптимальное управлении на 3ем с конца шаге должно быть таким, что при распределении оставшихся 3х единиц ресурса выдерживался принцип оптимальности при этом Х3=2 Х1=3 Остальные 0

В этом случаи

Э =16(1-е^-0,1*3)+14(1-е^-0,1*2)=6,68

суммарный эффект.

Резюме:

Изложенный алгоритм динамического программирования применительно к задачам распределения ресурсов по этапам производственного позволяет в соответствии с принципом Басмана получить оптимальное управление по всему плану путем получения условно – оптимальных управлений на каждом из его этапов и шагов.

Лекция 16. Нелинейное программирование в задачах

распределения разнородных ресурсов.

Нелинейное программирование (НП) – это математические методы определения max или min целевой функции при наличии ограничений в виде неравенств или уравнений.

Целевая функция или хотя бы одно из ограничений – нелинейное.

Смысл решения задач НП заключается в определении условий, обращающих ЦФ в экстремум.

Нелинейное программирование НП – это метод выбора наилучшего плана распределения неоднородных ресурсов, доставляющий экстремум ЦФ.

Методом НП решаются задачи распределения неоднородных ресурсов при следующей формулировке её в общем виде.

Постановка задачи

Пусть имеется m разнородных ресурсов, которое предполагается распределить по n потребителям.

Известны либо оценочные, либо вероятностные возможности переработки i-ого ресурса j-ым потребителем, а так же эффективность использования Э_ij

Распределение ресурсов по потребителям характеризуется параметром управления

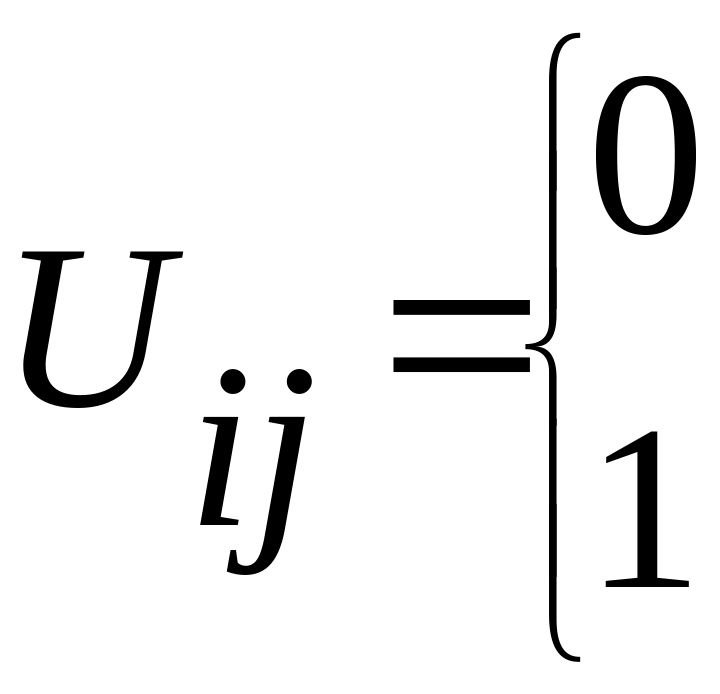, где 0 – если i-ый ресурс не направляется j-ому потребителю, а 1 –наоборот

Требуется распределит ресурсы по потребителям так (т.е. выбрать такие значения U_ij), что бы величина:

1. суммарной эффективности использования всех видов ресурсов была max.

2. полной вероятности достижения целевой функции была max.

Рассмотрим первый случай .

Для него 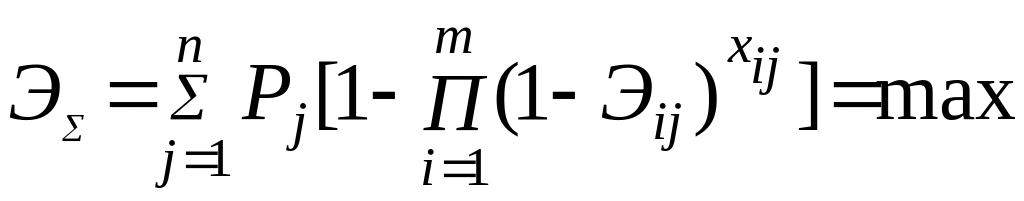(16.1)

Где x_ij –кол-во ресурсов i-ого типа, назначенные j-ому потребителю при ограничения (16.2)

Где N_i – кол-во единиц ресурса i-ого вида

Задача

Даны 2 группы разнородных ресурсов (m=2), которые можно включить в 3 проекта (n=3)

В первой группе ресурсов 6 единиц (N₁=6); во второй группе – 10 ед. (N₂=10).

Оценки важности проектов заданы таблицей.

Проекты	1	2	3
Pj – оценка	0,3	0,2	0,5

Эффективность вложений ресурсов различного рода Э_ij задана в таблице

Номер групп ресурсов	Номера проектов
	1	2	3
1	0,4	0,1	0,5
2	0,2	0,4	0,2

Распределение ресурсов по проектам характеризуется исходной матрицей

А = ||X_ij||

Требуется распределить по проектам разнородные ресурсы так, чтобы Э_Σ=max

Решение выполняется итерационным процессом

Алгоритм решения:

1. В области изменения максимизирующей функции определяется исходная отправное допустимое решение Э_ij удовлетворяющая ограничительные условия задачи.

2. с помощью специального Е критерия проверяется достаточно ли близко полученное решение к оптимальному (жилаемому).

3. если полученное отклонение 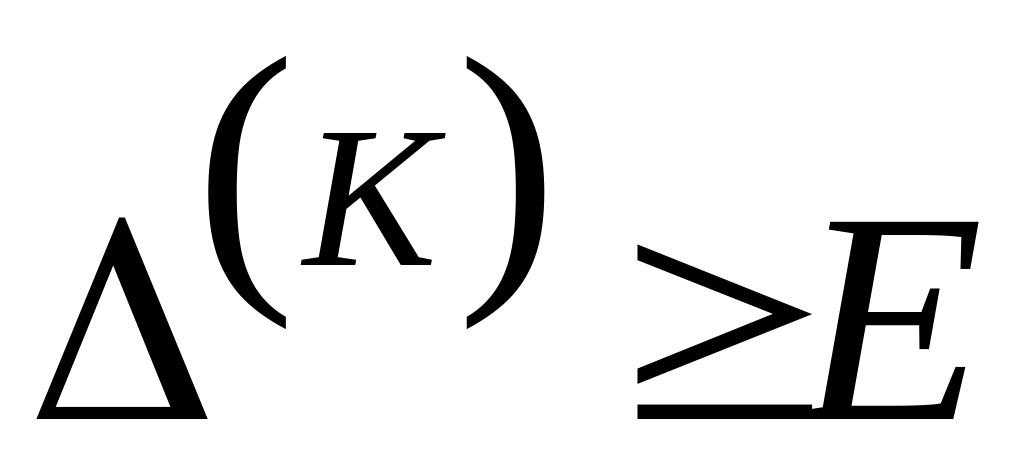, то путём построения, так называемого, возможного направления и определения в этом направлении конечного шага приближения к оптимуму, получают новое допустимое решение, которое увеличивает значение макс.функции.

4. процесс расчётов носит характер итерации, до полученного решения с минимальным отклонением (min^(K)>Δ). это и будет решение близкое с заданной точностью приближения Е.

реализация расчётов по алгоритму.

1. определяется отправное допустимое решение А⁽⁰⁾=||x_ij⁰||

где, А⁰ – матрица, характеризующая отправное распределение ресурсов по проектам.

Примечание: в качестве отправного распределения может быть взято любое (и произвольное в том числе) распределение с ограничительным условием задачи.

Чем отправное распределение ближе к оптимальному, тем меньше итераций понадобится.

Берём произвольно

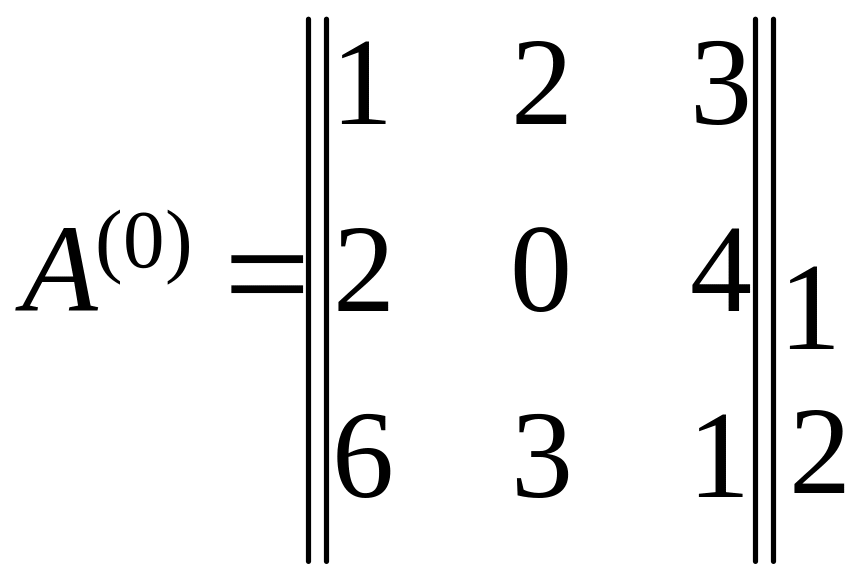
Столбцы – номера проектов

Строки – номера видов ресурсов

Далее осуществляется итерационная процедура. В результате выполнения к – итераций, получается К-ое приближение к оптимальному.

2. Определяется компонента матрицы возможного направления итерационных шагов, имеющая вид:

S^(K)=||S_ij^(K)||, где S_ij^(K)=

Величина находится с помощью матрицы y_ij^(K).

Резюме: при заданном Е критерии 0,01 необходимо после шага 4 итерации. В которых Δ^(K) больше Е кроме 4-ой итерации.

Точность приближения к оптимуму определяются ЛПР и Е может ровняться и 0,02; и 0,01; и 0,1; и 0,2.

Примечание : в курсовых проектах точность должна быть не менее 0,1.