5.5. Линейная корреляция

 

Если пары значений изучают с целью выявления линейной зависимости и при этом и не рассматривают соответственно как зависимую и независимую переменные, то в этом случае говорят о корреляции. Например, рост пар сестер имеет статистическую зависимость. Однако было бы бессмысленным рост одной сестры рассматривать как свободную, а рост другой — как зави­симую переменную. Такая же постановка вопроса имеет место, например, при сопоставлении давления воздуха, атмосферных осадков или температуры в различных местах.

Если пары значений нанести на - - диаграмму и искать прямую, которая изображает возможную линейную зависимость, то можно использовать метод наименьших квадратов. Имеют смысл две прямые, так как каждая переменная в равной мере может быть рассмотрена и как зависимая, и как независимая.

Если рассматривают функцию , то коэффициент b₁ выбирают так, чтобы сумма всех квадратов была бы минимальной. Однако с теми же основаниями величина у может рассматриваться как свободная переменная. Тогда коэффициент b₂ функции выбирают так, чтобы минимальной была сумма всех квадратов = В общем случае обе прямые не совпадают.

Можно показать, что обе величины b₁ и b₂ тем сильнее стремятся к нулю, и, следовательно, приближаются друг к другу, чем более независимы друг от друга и . При полной статистической независимости прямые перпендикулярны и b₁ = b₂ = 0.

Если имеет место функциональная зависимость в математическом смысле, то = 1/ и обе прямые регрессии совпадают.

Коэффициенты крутизны b₁ и b₂ в зависимости от степени (тесноты) статистической связи изменяются между нулем и значе­нием крутизны соответствующей линейной функциональной зависимости. Поэтому значения b₁ и b₂ в какой-то мере отражают тесноту линейной связи. Однако полностью охарактеризовать ее они не могут, так как не зафиксирована верхняя граница b. Этого можно достичь посредством нормирования. Нормированный следующим образом коэффициент r называется коэффициентом корреляции:

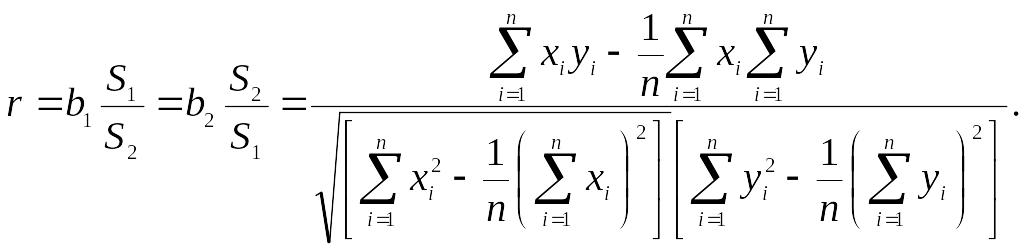(6.2)

Коэффициент, корреляции r может принимать значения только между -1 и +1. При строгой (функциональной) линейной связке и пары значений ( лежат на прямой. При положительном коэффициенте угла наклона прямой имеем r= +1, а при отри­цательном r= -1. Если и у полностью статистически независимы, то r = 0.

Модуль коэффициента r является мерой линейной зависимости. Чем ближе пары значений расположены к прямой, тем в большей степени модуль r приближается к единице.

Здесь необходимо сделать три замечания, чтобы избежать ошибочной интерпретации.

1. Из сказанного вытекает, что, если две величины не зависят друг от друга, то они не коррелированы и r = 0; если пары величин ( лежат на прямой, то r= 1.

Однако обратные утверждения в общем случае не верны. Если r = 0, то это означает, что отсутствует линейная зависимость. Но это не означает, что и у вообще не зависят друг от друга.

Если r = 1, то из этого не следует, что зависимость между и у линейна, а только то, что эти величины зависят друг от друга.

2. Если r используется как мера линейной зависимости, то необходимо учитывать, что r зависит от объема выборки n. Очевидно, что npи наличии только двух пар величин r всегда равен единице. Однако, как мы увидим при определении доверительных границ, при малых n доверительный интервал увеличивается и использование r в качестве статистической характеристики только при двух парах значений недопустимо.

3. Если пары значений лежат вблизи прямой, то из того, что r принимает значение, близкое ±1, не следует, что эта линейная зависимость отображает также причинно-следственную связь. Например, одновременно увеличиваются и средняя продолжительность жизни, и число жертв движения. Весьма вероятно, что имеется корреляция между числом совершаемых краж и числом автомобилей в определенной стране, так как и то и другое увеличивается. Возможно, что такая мнимая, лишенная смысла корреляция, происходит от того, что коррелированные явления имеют общую причину, однако так бывает не всегда. Гипотеза наличия причинно-следственной связи должна быть обоснована в каждом отдельном случае, Корреляция показывает лишь то, не противоречат ли полученные резуль­тата этой гипотезе.

Коэффициент корреляции r, рас­считанный по уравнению (6.2), характеризует корреляцию в выбор­ке. Он может быть использован в качестве оценки математического ожидания коэффициента корреля­ции генеральной совокупности. При этом снова возникает задача стати­стической достоверности этого коэффициента.

Наиболее просто проверить гипотезу = 0. При этом проверяют, является ли отличие коэффициента корреляции r от нуля статистически значимым. Однако эта проверка равнозначна проверке стати­стической значимости отличия от нуля коэффициентов b₁ пря­мой регрессии у — = b₁ . Поэтому она может быть осуществлена в соответствии с процедурой, изложенной выше.

Доверительный интервал для коэффициента корреляции опре­деляют следующим образом:

1. Выбирают доверительную вероятность Р (например, 95,99 % и т. п.).

2. По результатам, представленным на рис.5.1 статистической надежности определяют величину вычисляют и определяют с.

3. Определяют коэффициент корреляции

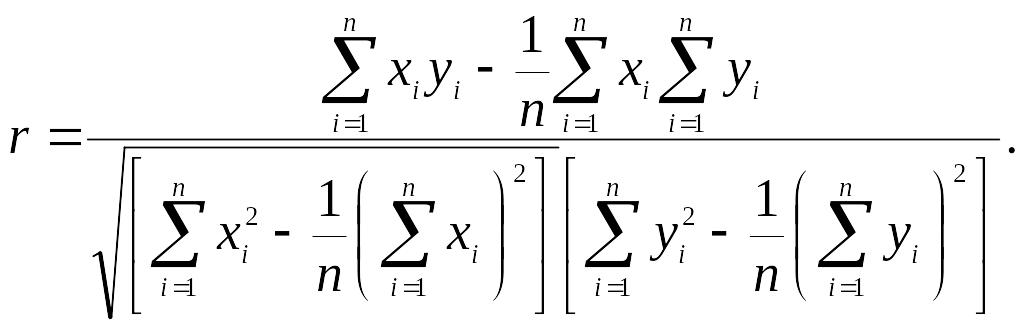
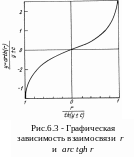
4. По результатам исследований (рис. 6.3) определяют зависимость

5. Еще раз, используя результаты, представленные на графике (рис. 6.3), определяют вели­чины:

6. Доверительный интервал для будет равен .