
- •(Для студентов специальности 7.010104 “Профессиональное обучение. Промышленное, гражданское и сельскохозяйственное строительство”)
- •Оглавление
- •1. Исследовательская и изобретательская деятельность
- •1. 1. Понятие о научно-исследовательской работе.
- •2. Основы измерения физических величин
- •2.2. Основные понятия об измерениях физической величины Блок-схема процесса измерения
- •2.3. Прямые и косвенные методы измерения
- •2.4. Аналоговые и цифровые методы измерений
- •2.5. Непрерывные и дискретные методы измерения
- •2.6. Методы отклонения и компенсационный метод
- •2.7. Классификация средств измерений
- •2.8. Структура измерительных приборов
- •2.9. Метрологические характеристики средств измерения
- •3. Погрешности измерений и их причины
- •3.1. Представительность измеряемой величины
- •3.2. Погрешности, связанные с процессом измерения
- •3.3. Погрешности, связанные с обработкой измеренных величин
- •3.4. Погрешности измерительных устройств
- •4. Статические погрешности измерений
- •4.1. Виды погрешностей
- •4.2. Случайная погрешность отдельного измерения
- •4.3. Случайная погрешность среднего значения
- •4.4. Систематическая погрешность
- •4.5. Распространение погрешностей
- •5. Способы обработки результатов измерений с учетом статистических погрешностей
- •5.1. Проверка гипотезы нормальности распределения
- •5.2. Грубые погрешности измерения и их отсеивание
- •5.3. Различие средних значений
- •5.4. Линейная регрессия
- •5.5. Линейная корреляция
- •5.6. Автоматическая коррекция погрешности
- •6. Динамические погрешности измерений
- •6.1. Измерение как процесс передачи сигналов
- •6.2. Сигналы и их математическое описание
- •6.3. Временные характеристики детерминированных сигналов
- •6.4. Временные характеристики стохастических сигналов
- •6.5. Частотные характеристики периодического сигнала
- •6.6. Частотные характеристики апериодического сигнала
- •6.7. Частотные характеристики стохастического сигнала
- •6.8. Дискретные сигналы
- •6.9. Динамические погрешности измерения
- •7.2. Погрешности отображения (преобразования) физической величины
- •7.3. Способы и средства первичного преобразования физической величины
- •7.4. Виды первичных преобразователей
- •7.5. Эффекты и чувствительные элементы, используемые для первичного преобразования
- •7.6. Измерительные преобразователи с электронным цифровым выходным сигналом
- •8. Приборы выдачи информации
- •8.1. Аналоговые приборы выдачи информации
- •8.2. Приборы выдачи цифровой информации
- •8.3. Дискретно-аналоговые преобразователи
- •8.4. Печатающие устройства для результатов измерений
- •8.5. Электронно-лучевые визуальные приборы
- •9. Способы и средства измерения продольных деформаций, наклепа и остаточных напряжений
- •9.1. Электрические способы измерения деформаций
- •Индуктивные тензометры
- •9.2. Механические способы измерения деформаций
- •9.3. Визуальные методы оценки деформаций
- •Литература
4.5. Распространение погрешностей
Если результат измерения определяется на основе математической обработки отдельных измеряемых величин, то погрешность вводится и в этот результат. Поэтому говорят о распространении погрешности. Различным структурам систематических и случайных погрешностей соответствуют разные законы распространения погрешностей.
4.5.1.
Систематические погрешности. Результат
измерения
![]() определяется по
определяется по
![]() различным измеренным величинам
i
. В статике
эта связь в общем виде описывается
уравнением
различным измеренным величинам
i
. В статике
эта связь в общем виде описывается
уравнением
= f ( ,..., i,... ) .
При малых отклонениях отдельных измеренных величин результирующее отклонение можно рассчитать, используя ряд Тейлора:
![]()
![]() .
.
Если
под малыми отклонениями
![]() понимать систематическую погрешность
Еs
понимать систематическую погрешность
Еs![]() ,
т.е. отклонение от действительного
значения, то систематическая погрешность
результата измерения определяется по
следующей формуле:
,
т.е. отклонение от действительного
значения, то систематическая погрешность
результата измерения определяется по
следующей формуле:
Е![]()
Следует отметить, что систематическая погрешность может иметь знак плюс или минус, вследствие чего возникает возможность её компенсации.
Особое
значение для требований, предъявляемых
к систематическим погрешностям, имеют
частные производные
![]() .
Эти коэффициенты воздействия, или
весовые коэффициенты, показывают, с
каким весом отдельные систематические
погрешности участвуют в образовании
систематической погрешности результата
измерения.
.
Эти коэффициенты воздействия, или
весовые коэффициенты, показывают, с
каким весом отдельные систематические
погрешности участвуют в образовании
систематической погрешности результата
измерения.
4.5.2.Случайные
погрешности. Случайная
погрешность, рассматриваемая как
единичное явление по своей природе не
может быть предсказана заранее. Однако
можно высказать суждение о её статистических
свойствах. При нормальном распределении
погрешности среднеквадратичное
отклонение
является мерой, характеризующей плотность
распределения погрешности. Поэтому
вопрос о распространении погрешности
сводится к способу распространения
статистической характеристики
или
доверительных границ. В этом случае
требуется определить среднеквадратичное
отклонение
![]() результата измерения
результата измерения
![]() при известных среднеквадратичных
отклонениях
при известных среднеквадратичных
отклонениях
![]() влияющих величин
влияющих величин
![]() .
.
Если
отдельные влияющие величины взаимно
независимы и для среднеквадратичных
отклонений справедливо неравенство
![]() «
,
то
«
,
то
![]() можно вычислить по следующей формуле:
можно вычислить по следующей формуле:
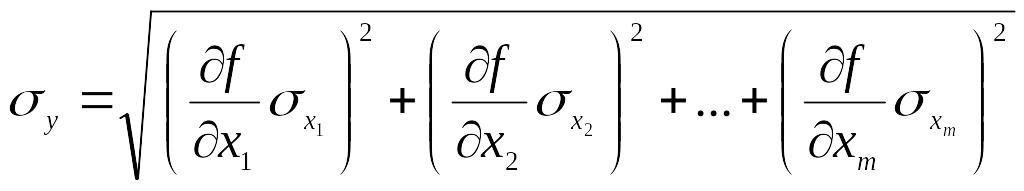
Если
вместо среднеквадратичных отклонений
представить их оценки – рассеяния
![]() ,
то получим соотношение (правда, не
строгое) для определения
,
то получим соотношение (правда, не
строгое) для определения
![]() результата
измерения:
результата
измерения:
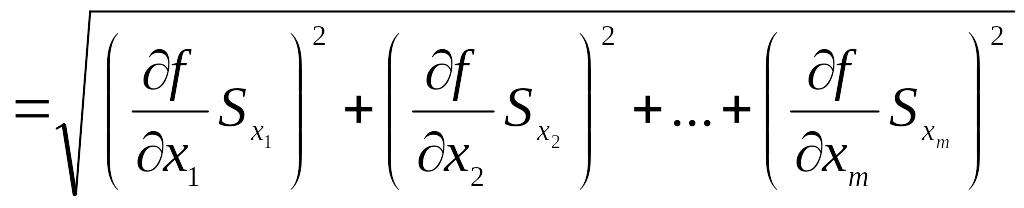 .
.
Для увеличения точности расчёта результата измерения можно использовать средние значения влияющих величин:
![]()
Если
для усреднения каждой из
влияющих
величин использованы по
![]() значений, то среднеквадратичное
отклонение или рассеяние уменьшается
согласно (5.1):
значений, то среднеквадратичное
отклонение или рассеяние уменьшается
согласно (5.1):
![]() или
или
![]() .
.
Если рассеяние влияющих величин заранее неизвестно, то можно определить его одновременно с усреднением , используя те же значений. Доверительные границы погрешности среднего результата измерения определяют по формуле:
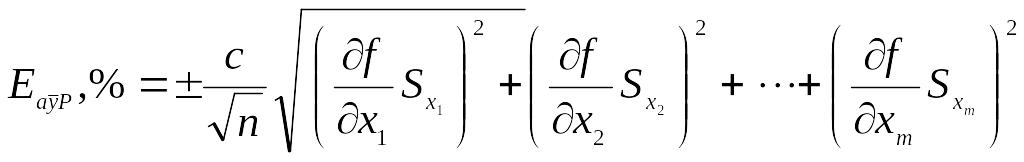 .
.
Величину
![]() определяют по рис. 1.3-8 для выбранной
доверительной вероятности Р
(%) и при числе
степеней свободы
определяют по рис. 1.3-8 для выбранной
доверительной вероятности Р
(%) и при числе
степеней свободы
![]() =
n
–1.
=
n
–1.
4.5.3. Предел погрешности. Предел погрешности применяют для задания максимального гарантированного значения погрешности. Этот предел содержит как оценённую систематическую, так и случайную погрешность. Пределы погрешностей отдельных измеренных величин могут иметь положительные, отрицательные или неопределённые знаки. При неопределённых знаках предел погрешности результата измерения определяется суммированием абсолютных величин пределов погрешности отдельных измеренных значений:
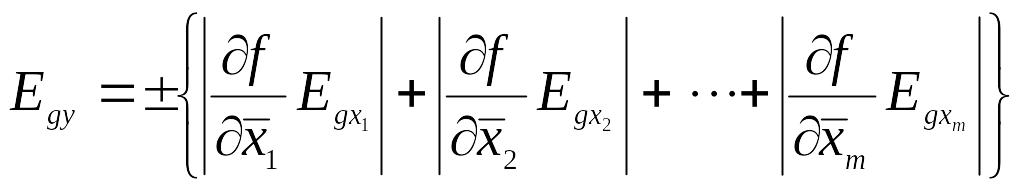 .
.
Если знаки пределов погрешности измеренных величин известны, то положительный и отрицательный пределы погрешности результата измерения вычисляются отдельно:
![]() ;
;
![]()
![]() ;
;
![]()
