5. Главное значение интеграла 1-го рода

Определение 3. Пусть f(x) определена на (-∞, ∞) и интегрируема на любой конечной части. Тогда интеграл в смысле главного значения есть от сокращения ее французского названия.

Пример 30. Пусть f(x)=x. Тогда , но не существуетть на основе формулы Ньютона–Лейбница и по определению .Отметим: сходимость интеграла влечет существование V.P. интеграла, но не наоборот, что иллюстрирует пример 30.

6. Несобственный интеграл 2-го рода

Определение 4. Пусть f(x) определена на [a, b), неограничена слева от b, интегрируема на любом и существует . Тогда этот предел называется несобственным интегралом 2-го рода от f(x) на [a, b), обозначается и говорят, что сходится, а f(x) интегрируема в несобственном смысле на [a, b). Если предел не существует, то расходится, а f (x) не интегрируема в несобственном смысле.

Замечание 8. Геометрический смысл для – это площадь неограниченной криволинейной трапеции под графиком f(x) на [a, b) . Если же f (x) ограничена на [a, b), то равен обычному интегралу Римана на [a, b]. Отметим, что если f(x) неограничена только в окрестности точки а, то несобственный ..

Точки a, b в окрестности которых f(x) неограничена, называют еще особыми точками для f(x). Если f(x) имеет особую точку с на [a, b] и интегрируема на [a, c) и (c, b], то f(x) называется интегрируемой в несобственном смысле на [a, b] и . Аналогично индуктивно определяется интеграл для n особых точек на [a, b]. Свойства интеграла:

1. Линейность. Если и сходятся, то для любых чисел λ, μ сходится .

2. Замена переменной. Пусть f(x) определена на [a,b) и b - особая точка и f(x) непрерывна на [a,b), а непрерывно дифференцируема на и , где . Тогда интеграл и они сходятся или расходятся одновременно.

3. Интегрирование по частям. Если f(x) и g(x) непрерывно дифференцируемы на [a, b) и - существует, то и . Эта формула справедлива, если существует хотя бы один из входящих в нее интегралов. Если же какой-либо из них расходится, то расходится и другой.

4. Формула Ньютона–Лейбница. Если f(x) определена на [a, b) и непрерывна, а b – особая точка и F(x) какая-либо ее первообразная на [a, b), то , где F(b-0) односторонний предел слева в точке и интеграл существует, если существует F(b-0).

5. Интегрирование неравенств. Если f(x) и g(x) интегрируемы на [a, b) в несобственном смысле и на [a, b), то верно . Для и имеем .

Замечание 9. Все вышеизложенные свойства верны и в случае, когда для f(x), g(x) особая точка а на (a, b]. Изменения здесь очевидны.

Пример 31. Исследовать . Решение. Для особая точка а. Если , то особой точки нет и интеграл определенный по Риману. Здесь для и при , а при и искомый интеграл сходится. Если , то и интеграл расходится. При имеем и при будет . Отсюда расходится. Итак, искомый интеграл сходится для и расходится для . Аналогично рассуждая, интеграл сходится для и расходится для .

Пример 32. Вычислить . Решение. Очевидно, имеем и для всех подинтегральных функций и a = 0. Тогда по примеру 31 получаем сходимость и .

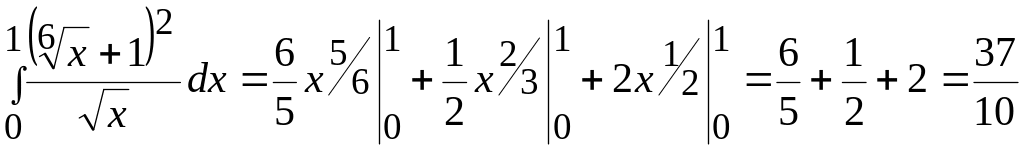Пример 33. Вычислить . Решение. Здесь 1 – особая точка. Заменим 1 – x = t², t > 0. Тогда x = 1 – t² и dx = - 2 t dt и пределы интегрирования α = 1, β = 0. Здесь функция , а . Очевидно, - непрерывно дифференцируема. Тогда по формуле замены переменной имеем .

Пример 34. Вычислить: . Решение. Положим , а . Тогда и ибо для μ > 0..

Пример35. Доказать .Решение. Имеем на [0, 2), где x₀ = 2 особая точка для подинтегральной функции,

оценки , ибо на [0, 2) функция , а и . Поэтому получаем . Но . Отсюда .

Пример 36. Вычислить для a < b. Решение. Здесь две особые точки: a и b. При замене переменной можно, не разделяя точки (т.е. не рассматривая , где a < c < b), подсчитать искомый интеграл. При , где и точки , соответствуют a и b, получаем , , . Тогда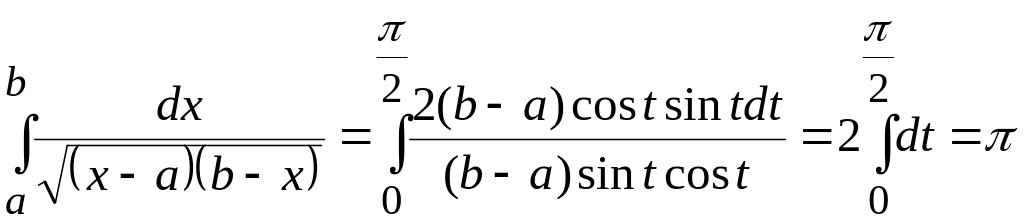 . Пример 37. Вычислить или установить расходимость .

Решение. Подинтегральная функция неограничена только в правой окрестности a = - 1. В левой окрестности точки b = 1 функция ограничена, так как предел по правилу Лопиталя. Тогда .