
- •Ознайомлення з діями множення і ділення
- •Дія множення
- •2. Різні підходи до складання та засвоєння таблиць множення і ділення
- •3. Прийоми закріплення таблиць множення і ділення
- •4. Методика ознайомлення з поняттями «більше в ….», «менше у …»; кратне порівняння чисел
- •5. Залежність результату множення і ділення від зміни одного з компонентів при сталому іншому.
Методика вивчення дій множення і ділення. Табличне множення і ділення
Лекція – 2 год
План лекції
Ознайомлення з діями множення і ділення
Різні підходи до складання та засвоєння таблиць множення і ділення
Прийоми закріплення таблиць множення і ділення
Методика ознайомлення з поняттями «більше в ….», «менше у …»; кратне порівняння чисел
5. Залежність результату множення і ділення від зміни одного з компонентів при сталому іншому.
Опорний конспект
Витяг з програми
Зміст навчального матеріалу |
Державні вимоги до рівня загальноосвітньої підготовки учнів |
Табличне множення та ділення
Арифметичні дії множення і ділення Сутність дії множення. Сутність дії ділення. Знаки арифметичних дій множення і ділення. Назви компонентів та результатів дій множення і ділення. Переставний закон множення. Взаємозв’язок між множенням і діленням. Властивості множення і ділення на 1, 10; множення на нуль, нуля на число; ділення нуля на число Неможливість ділення на нуль. Ділення рівних чисел.
|
знає назви компонентів та результатів дій множення і ділення; знає властивості дій множення і ділення на 1,10, множення на нуль, нуля на число, ділення нуля на число, ділення рівних чисел; розуміє що ділення на 0 неможливе; розуміє сутність дії множення як операцію об’єднання множин, які не перетинаються і містять однакову кількість елементів; розуміє, що суму однакових доданків можна замінити множенням; розуміє сутність дії ділення як операцію розбиття множини на кілька рівночисельних множин, що не перетинаються; розрізняє ділення на вміщення і ділення на рівні частини; застосовує взаємозв’язок між діями множення і ділення в обчисленнях; застосовує в обчисленнях переставний закон множення |
Таблиці множення і ділення Таблиці множення та ділення одноцифрових чисел. Залежність результату множення і ділення від зміни одного з компонентів при сталому іншому. Перевірка правильності виконання дій множення і ділення
|
знає таблиці множення чисел 2–9; знає таблиці ділення на числа 2–9; розуміє способи складання таблиць множення і ділення; розуміє залежність значення добутку від зміни одного з множників; розуміє залежність значення частки від зміни діленого або дільника; перевіряє правильність виконання дії множення діленням, а ділення – множенням |
Відношення кратного порівняння Збільшення та зменшення числа в кілька разів. Кратне порівняння чисел.
|
знає слова-ознаки відношення кратного порівняння; розуміє сутність відношення «більше в...», «менше в...»; моделює відношення кратного порівняння чисел |
Правила знаходження невідомих компонентів дій множення і ділення Знаходження невідомих множника, діленого, дільника |
застосовує в обчисленнях правила знаходження невідомих множника, діленого, дільника |
Ознайомлення з діями множення і ділення
Ознайомлення з діями множення і ділення відбувається за одною схемою:
– розглядається задача, що розкриває зміст дії;
– записується приклад, що дає розв’язання цієї задачі з відповідним коментуванням вчителя щодо позначень, запису і читання;
–опрацьовуються вправи на закріплення з поняттям дії, що вводиться.
а) Дія множення
Проводиться через задачу на знаходження суми однакових доданків.
Потрібно обчислити кількість розташованих парами кружечків (вишеньок)
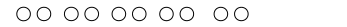
2 + 2 + 2 + 2 + 2 = 10
Знаходження суми однакових доданків називається множенням. 2 · 5 = 10. На першому місці записується число, що додається, на другому – число, яке показує. Скільки таких доданків є. між ними ставиться знак дії множення «·». Після знака «=» пишемо результат, тобто, значення суми.
б) Дія ділення
Задачі 1.( ділення на рівні частини) 6 груш розділили порівну на 3 тарілки. По скільки груш клали на кожну тарілку?
Розв’язування задачі супроводжується демонстрацією ситуації, описаної в задачі. Груші ділимо по одній по черзі у кожну тарілку. Після закінчення поділу рахуємо кількість груш у кожній тарілці. Груші ділили порівну. Над числами 6 і 3 виконується дія ділення, знак якої «:», запис має вид: 6 : 3 = 2.
Задача 2. (ділення на вміщення) 6 груш розклали по 3 груші на тарілки. Скільки тарілок заповнили?
При демонстрації ситуації груші відраховуємо по 3 і кладемо на тарілок. Після закінчення операції рахуємо кількість тарілок. У цьому випадку груші також ділили. Тому ця задача також розв’язується дією ділення 6 : 3 = 2. Але у цій задачі число 2 уже означає кількість заповнених тарілок.
в) Зв'язок між компонентами та результатами арифметичних дій множення і ділення.
Дія множення
-
4 · 6 = 24
24 : 6 = 4
24 : 4 = 6
Складаємо приклад на множення, рахуючи прямокутники по стовпчиках:
Складаємо приклади на ділення. Ділячи квадратики спочатку на 6 стовпчиків, а потім – на 4 рядки.
Висновок: З кожного прикладу на множення можна скласти два приклади на ділення.
Пригадуємо назви чисел при множенні: 4 і 6 – множники, 24 – добуток. Аналізуємо записи прикладів на ділення і робимо
Висновок: Якщо добуток поділити на один із множників, одержимо другий множник.
Перевірка правильності виконання дії множення: Щоб перевірити правильність виконання дії множення, можна добуток поділити на один з множників. Якщо отримаємо другий множник, то дія множення виконана правильно.
Дія ділення.
28 : 4 = 7
Прочитайте приклад на ділення. Як називається число 28? Число 4? Число 7?
Завдання: Дільник помножити на частку. Що одержимо? (При множенні дільника на частку (частки на дільник), отримаємо ділене).
Правило перевірки правильності виконання дії ділення за допомогою дії множення: Щоб перевірити правильність виконання дії ділення, можна дільник помножити на частку (частку помножити на дільник). Якщо одержимо ділене, дія ділення виконана правильно.
2) 32 : 4 = 8
Завдання: Поділити ділене на частку. Що одержимо? (При діленні діленого на частку одержимо дільник).
Правило перевірки правильності виконання дії ділення за допомогою дії ділення: Щоб перевірити правильність виконання дії ділення, можна ділене поділити на частку. Якщо одержимо дільник, то дія ділення виконана правильно
