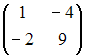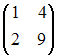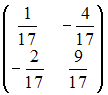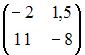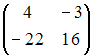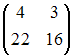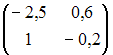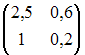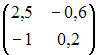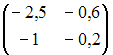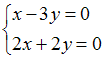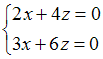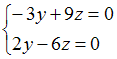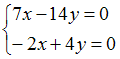- •1.1. Вычисление определителей
- •1.2. Линейные операции над матрицами
- •1.3. Умножение матриц
- •1.4. Ранг матрицы
- •1.5. Обратная матрица
- •1.6. Системы линейных уравнений
- •2.1. Прямоугольные координаты на плоскости
- •2.2. Полярные координаты на плоскости
- •2.3. Прямая на плоскости
- •2.4. Кривые второго порядка
- •2.5. Прямая и плоскость в пространстве
- •2.6. Поверхности второго порядка
- •3.1. Область определения функции
- •3.2. Предел функции
- •3.3. Производные высших порядков
- •3.4. Дифференциальное исчисление фнп
- •3.5. Основные методы интегрирования
- •3.6. Приложения определенного интеграла
- •4.1. Числовые последовательности
- •4.2. Сходимость числовых рядов
- •4.3. Область сходимости степенного ряда
- •4.4. Ряд Тейлора (Маклорена)
- •5.1. Типы дифференциальных уравнений
- •5.2. Дифференциальные уравнения с разделяющимися переменными
- •5.3. Линейные неоднородные дифференциальные уравнения первого
- •5.4. Задача Коши для дифференциального уравнения первого порядка
- •5.5. Линейные дифференциальные уравнения второго порядка с
- •5.6. Дифференциальные уравнения высших порядков, допускающие
- •6.1. Определение вероятности
- •6.2. Теоремы сложения и умножения вероятностей
- •6.3. Полная вероятность. Формулы Байеса
- •6.4. Законы распределения вероятностей дискретных случайных
- •6.5. Законы распределения вероятностей непрерывных случайных
- •6.6. Числовые характеристики случайных величин
1.5. Обратная матрица
Тема:
Обратная матрица
Дана
матрица
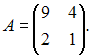 Тогда
обратная матрица
Тогда
обратная матрица
![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Обратная
матрица имеет вид
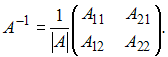 Вычислим
Вычислим
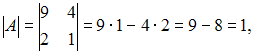
![]()
![]()
![]()
![]() Тогда
Тогда
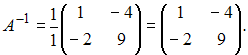
Тема:
Обратная матрица
Дана
матрицы
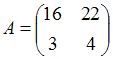 .
Тогда матрица
.
Тогда матрица
![]() равна …
равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Транспонируем
данную матрицу
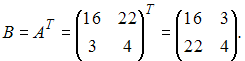 Обратная
матрица имеет вид
Обратная
матрица имеет вид
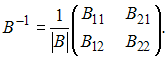 Вычислим
Вычислим
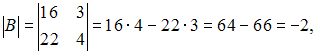
![]()
![]()
![]()
![]() Тогда
Тогда
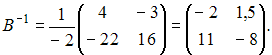
Тема:
Обратная матрица
Для
матрицы
 не
существует
обратной, если значение
не
существует
обратной, если значение
![]() равно …
равно …
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
– 2 |
Решение:
Матрица
не имеет обратной, если определитель
матрицы равен нулю, то есть
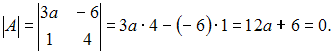 Тогда
обратной матрицы не существует при
Тогда
обратной матрицы не существует при
![]()
Тема:
Обратная матрица
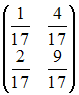
Дана
матрица
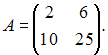 Тогда
обратная матрица
имеет
вид …
Тогда
обратная матрица
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Обратная
матрица имеет вид
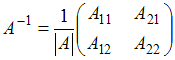 .
Вычислим
.
Вычислим
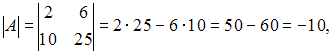
![]()
![]()
![]()
![]() Тогда
Тогда
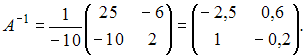
1.6. Системы линейных уравнений
Тема:
Системы линейных уравнений
Если
![]() и
и
![]() являются
решением системы линейных уравнений
являются
решением системы линейных уравнений
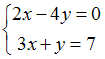 ,
то их разность
,
то их разность
![]() равна …
равна …
|
|
|
1 |
|
|
|
– 1 |
|
|
|
2 |
|
|
|
– 2 |
Решение:
Если
определитель матрицы системы не равен
нулю, то решение системы линейных
уравнений
 по
правилу Крамера находится в виде:
по
правилу Крамера находится в виде:
![]() ,
,
![]() ,
где
,
где
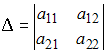 ,
,
 и
и
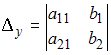 .
Тогда
.
Тогда
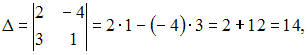
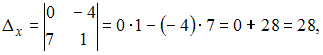
 и
и
![]()
![]() Следовательно,
разность равна
Следовательно,
разность равна
![]()
Тема: Системы линейных уравнений Единственное решение имеет однородная система линейных алгебраических уравнений …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Однородная
система линейных алгебраических
уравнений имеет одно единственное
решение, если ее определитель не равен
нулю.
1) Из системы
,
получим
 так
как столбцы пропорциональны.
2) Из
системы
,
получим
так
как столбцы пропорциональны.
2) Из
системы
,
получим
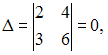 так
как строки пропорциональны.
3) Из
системы
,
получим
так
как строки пропорциональны.
3) Из
системы
,
получим
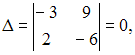 так
как строки пропорциональны.
4). Из
системы
,
получим
так
как строки пропорциональны.
4). Из
системы
,
получим
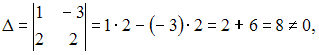 следовательно,
система имеет одно единственное решение.
следовательно,
система имеет одно единственное решение.
Тема:
Системы линейных уравнений
Система
линейных уравнений
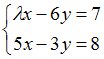 имеет
единственное решение, если
имеет
единственное решение, если
![]() не
равно …
не
равно …
|
|
|
10 |
|
|
|
– 10 |
|
|
|
2,5 |
|
|
|
– 2,5 |
Решение:
Система
линейных уравнений
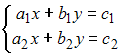 имеет
единственное решение, если определитель
матрицы системы
имеет
единственное решение, если определитель
матрицы системы
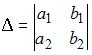 не
равен нулю. Вычислим
не
равен нулю. Вычислим
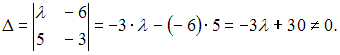 Тогда
Тогда
![]()
ДЕ 2. Аналитическая геометрия