Тема 5. Элементы математической статистики. Статистическая оценка параметров распределения
1. Генеральная и выборочные совокупности.
2. Статистическое распределение случайной величины.
3. Эмпирическая функция распределения. Графическое изображение статистических рядов.
4. Классификация точечных оценок. Метод моментов и метод наибольшего правдоподобия.
5. Доверительная вероятность, доверительный интервал. Интервальные оценки параметров распределения.
6. Статистический критерий значимости проверки нулевой гипотезы.
7. Статистическая проверка гипотез о параметрах распределения (математическом ожидании, равенстве математических ожиданий, дисперсии).
8. Статистическая
проверка непараметрических гипотез.
Критерии согласия
и Колмогорова.
9.Статистическая зависимость. Линейная регрессия. Метод наименьших квадратов.
10. Эмпирический коэффициент корреляции и его свойства.
Между составляющими
двумерной
может существовать зависимость, не
носящая функциональный характер. В этом
случае мы не можем говорить о том, какое
значение принимает одна составляющая,
если вторая приняла некоторое конкретное
значение, но мы можем говорить о законе
распределения (условном) одной
составляющей, если известно, какое
значение приняла вторая. Такая зависимость
называется статистической.
В практических приложениях при исследовании статистической зависимости СВ Х и Y рассматривают зависимость между значениями одной из них X и условным математическим ожиданием другой
(5.1)
Уравнение (5.1) называется модельным уравнением регрессии Y на X . Если эта зависимость линейная, т.е.
, (5.2)
то регрессия называется линейной.
Поскольку модельное уравнение регрессии неизвестно, то для его оценки используют эмпирическое уравнение регрессии
, (5.3)
где коэффициенты
и
находят
по результатам выборки
объема
методом наименьших квадратов, а именно
и
выбирают
так, чтобы они минимизировали функцию
.
Используя
необходимые условия экстремума
,
получают, систему уравнений:
И далее:
(5.4)
где
Решая
систему (5.4), получим
. (5.5)
После подстановки в формулу (5.3) значений и из (5.5) она примет вид:
,
где
(5.6)
Число
является выборочным коэффициентом
корреляции,
.
При этом число
(5.7)
называется коэффициентом детерминации.
Другая формула
для
:
. (5.8)
Поэтому
показывает долю разброса результатов
наблюдений
относительно прямой
,
которая объясняется выборочной регрессией
(5.3). При этом числа
в
формуле (5.8) называются остатками,
а число
(5.9)
- остаточной суммой квадратов.
Числа
и
,
полученные по методу наименьших квадратов
являются несмещенными оценками параметров
и
из (5.2), то есть
.
Число
(5.10)
называется остаточной дисперсией.
В качестве примера рассмотрим задачу из задания 5, исходные данные возьмем для варианта 31*(см. ниже).
Пример 5.1.
Решение. 1) Зависимость между X и Y будем искать в виде . Параметры и модели найдем из системы (5.4):
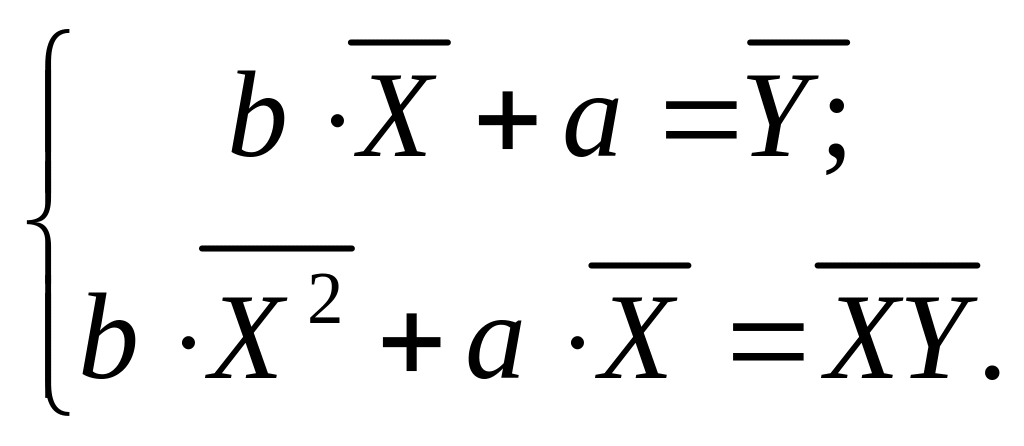
Тогда по формуле (5.5)
Из первого уравнения
.
Итак, уравнение
прямой линии регрессии Y
на x:
.
Вспомогательные вычисления соберем в таблицу.
xi |
yi |
xiyi |
xi2 |
yi2 |
ei2 |
4 |
2 |
8 |
16 |
4 |
0,2025 |
4,5 |
3 |
13,5 |
20,25 |
9 |
0,057121 |
5,5 |
3 |
16,5 |
30,25 |
9 |
0,146689 |
6 |
4 |
24 |
36 |
16 |
0,0936 |
6,5 |
4 |
26 |
42,25 |
16 |
0,00003 |
7 |
5 |
35 |
49 |
25 |
0,4679 |
7,2 |
5 |
36 |
51,84 |
25 |
0,31315 |
7,8 |
4 |
31,2 |
60,84 |
16 |
0,66194 |
8 |
5 |
40 |
64 |
25 |
0,00384 |
10 |
6 |
60 |
100 |
36 |
0,03313 |
=66,5 |
=41 |
=290,2 |
=470,43 |
=181 |
Qe=1,9799 |
|
|
|
|
|
s2=0,2475 |
2) Построим корреляционное поле и график ,
.
График линии регрессии
3) Вычислим
коэффициент корреляции
по формуле (5.4) и коэффициент детерминации
:
4) Коэффициент детерминации
(с
точностью до 0,01).
Поэтому 85% рассеивания зависимой переменной Y объясняется линейной регрессией Y на X, а 15% рассеивания Y остались необъясненными.
5) По формуле (5.9):
.
6) По формуле (5.10):
.
7) Подставим точку
в уравнение
,
(с точностью до 0,01).
8) Вычислим
по формуле (5.8), при этом используя
равенство
(с точностью до
0,01).
9) Если
;
то
,
т.е. при энерговооруженности
тыс. кВт час в год/ч можно ожидать среднюю
производительность
(тыс.изд.
в год/ч).