Задача № 2

От магистральной кабельной линии в цеху промышленного предприятия получают питание k групп электродвигателей (n₁, n₂, ..., n_k) с потребляемой мощностью: 1) aS₁ кВА, n₁=а; 2) bS₂ кВА, n₁=b; 3) …; n_n=k; … и одинаковым cos. Вероятность включения в работу каждого двигателя в группах соответственно р_i (p₁, p₂, ..., p_k). События включения в работу и отключения каждого двигателя в каждой группе – независимые.

Требуется определить вероятности нагрузки головного участка линии;

а) Н₁ = 0;

б) ;

в) .

Решение

Для определения вероятностей нагрузки головного участка используем схему независимых испытаний - биномиальный закон распределения.

а) Вероятность нагрузки головного участка, равная нулю, определяется при условии, что не включен ни один двигатель (в этом случае m_i=0).

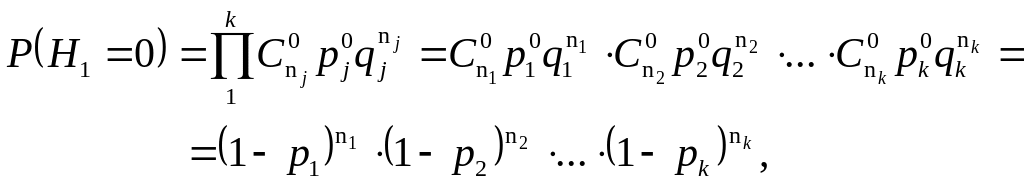
где (1-р_i) – вероятность отключенного состояния i-го двигателя;

  – число сочетаний из n элементов по m.

Для выполнения пунктов б) и в) необходимо выявить все случаи, когда нагрузка головного участка равна и больше (меньше) S₁ и определить эти вероятности.

Вероятность нагрузки головного участка Р( ) или Р( ) определяется по выражениям:

,

,

где М – количество случаев удовлетворяющих условию Н  S₁;

N – количество случаев удовлетворяющих условию Н < S₁.

Если число случаев очень велико, то задачу рекомендуется решить, учитывая противоположное состояние.

Рекомендации по выбору варианта

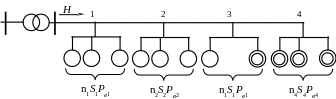
Рис. 2

Таблица 3

№ вар.	1			2			3			4
	n1	S1	Pв1	n2	S2	Pв2	n3	S3	Pв3	n4	S4	Pв4
1	2	3	0,5	3	4	0,6	4	5	0,7	2	7	0,4
2	4	3	0,4	5	5	0,3	3	2	0,6	2	5	0,6
3	2	10	0,3	3	5	0,4	3	15	0,5	4	10	0,6
4	3	5	0,4	2	10	0,5	4	5	0,3	3	15	0,7
5	2	3	0,8	3	5	0,4	4	2	0,6	5	5	0,4
6	5	10	0,7	3	5	0,6	2	15	0,5	4	5	0,4
7	4	15	0,6	6	10	0,5	3	15	0,4	2	10	0,7
8	2	7	0,5	4	5	0,4	6	3	0,7	3	4	0,6
9	3	15	0,4	2	10	0,7	4	15	0,6	6	10	0,5
0	5	5	0,6	3	5	0,6	2	3	0,2	4	2	0,4

Таблица 4

№ вар.

А О Э

Б П Ю

В Р Я

Г С

Д Т

Е У

Ж З Ф

И Х

К Ц

Л Ч

М Ш

Н Щ

1

>10

=22

<10

=21

=12

>54

>56

=54

=56

<54

<56

=25

2

>11

=11

<11

=12

>48

=43

<48

=48

=18

>10

<10

=10

3

<15

=15

>15

=55

=45

>25

=25

<25

4

=45

>25

=25

<25

>90

<90

=40

>15

<15

=60

=15

=105

5

>5

=5

<15

=15

>15

=8

=11

=25

=39

>39

<39

>50

6

>20

<20

=30

=50

=80

=40

=90

>95

=95

<95

>100

<100

7

>25

<25

>35

<35

=100

=120

=150

=140

=90

>150

<150

>140

8

=25

<56

<54

=56

=54

>56

>54

=12

=21

<10

=22

>10

9

>140

<150

>150

=90

=140

=150

=120

=100

=35

>35

<25

>25

0

>50

<39

>39

=39

=25

=11

=8

>15

=15

<15

=5

>5

Выбор количества электроприемников n_j, их величины S_j и вероятности включения каждого Р_вj определяется по таблице 3 в соответствии с последней цифрой зачетной книжки.

Расчетная вероятность Р(Н) выбирается по первой букве фамилии из таблицы 4, при соответствующем номере варианта исходных данных.

Например. Иванов Николая Иванович. Зачетная книжка № 87354. Исходные данные для расчета:

n₁=3, S₁=5, P_в1=0,4; n₂=2, S₂=10, P_в2=0,5;

n₃=4, S₃=5, P_в3=0,3; n₄=3, S₄=15, P_в4=0,7;

Р(Н) > 15.