Оборудование и материалы

1. Установка (рис.1) для проведения исследований, в которую входят: термостат 2, кварцевый стержень 5, индикатор 4, термометр 6, опоры 3.

2. Термобиметаллическая пластина (1).

Порядок проведения работы

1. Ознакомиться со схемой установки, показанной на рис.1.

2. Внести в таблицу 1 исходные температуру опыта t₀ и показания индикатора n₀ в мм.

Таблица 1

t, С
n, мм.

3. Включить термостат, фиксировать изменение стрелы прогиба пластины через каждые 20° до 160° С, внося результаты в таблицу 1.

4. На основании полученных данных рассчитать и занести в таблицу 2 величину стрелы прогиба пластины f_э = n_n- n₀ и приращения температуры Т = t_n- t₀.

Таблица 2

T, K
fэ, мм.
fр,, мм.

5. Построить экспериментальную кривую зависимости f_э от T.

6. Рассчитать и внести в таблицу 2 величину прогиба f_р . Построить на том же графике расчетную кривую зависимости величины прогиба f_р от Т в исследуемом интервале температур. При расчетах использовать следующие параметры ТБ пластины:

₁= 15·10^-6 К ^-1; ₂= 1,5·10^-6 К ^-1; h₁+h₂=2,4 мм; b= 160 мм.

Содержание отчета

1. Цель работы.

2. Схема установки.

3. Расчетная формула для определения стрелы прогиба f термобиметаллической пластины.

4. Заполненная таблица 2.

5. График зависимости f_э и f_р от T.

Контрольные вопросы

1. Что называется термобиметаллами?

2. Из каких материалов изготовляются пассивный и активный слои термобиметалла?

3. Какие основные требования предъявляются к термобиметаллу?

4. Какими параметрами оценивается температурная чувствительность термобиметалла?

5. Какие напряжения возникают вблизи границы соединения слоев термобиметалла?

6. Где применяются термобиметаллы?

Литература

1. Пятин O.K. Материалы в приборостроении и автоматике. - М.: Машиностроение, 1969, гл. 5, с.301, 317—321.

2. Феодосьев В.И. Избранные задачи и вопросы по сопротивлению материалов. - М.: Машиностроение, 1953, с. 127.

Часть 4. Теплопроводность металлических материалов

Цель работы: определить коэффициент теплопроводности металла.

Содержание работы

В твердых телах происходит самопроизвольный перенос тепла от более нагретых частей тела к менее нагретым, интенсивность которого обусловлена способностью материала проводить тепло.

Явление теплопроводности учитывается при термообработке, расчете тепловых режимов работы деталей и изделий или используется для обеспечения подвода и отвода тепла, для равномерного распределения температуры в деталях, а также в целях тепловой изоляции.

В изотропном твердом теле распространение тепла в направлении x, перпендикулярном некоторой площади S, описывается уравнением Фурье:

(d Q/dt)/S = – dT/dx,

где dQ – количество тепла, проходящее за время dt через площадь S; Т – температура;  – коэффициент теплопроводности. Знак “минус” означает, что поток тепла направлен против градиента температуры dT dx, то есть от горячей области к холодной.

В твердых телах имеют место два основных механизма переноса тепловой энергии:

- за счет связанных тепловых колебаний атомов;

- электронами проводимости.

Связанные колебания атомов относительно положений равновесия можно рассматривать как совокупность распространяющихся в теле упругих волн.

Частота колебаний (длина волн) и соответствующая им энергия могут принимать только определенные (дискретные) значения. Это позволяет, по аналогии с квантовой теорией света, представить такие колебания (моды) как подвижные квазичастицы – фононы, заполняющие объем тела в виде газа. Фононы при своем движении сталкиваются с другими фононами (фонон-фононное взаимодействие) и со статическими дефектами, теряя при этом энергию. Как и в случае рассмотрения процессов переноса в классическом газе теплопроводность _реш, обусловленную переносом энергии фононным газом, можно записать как:

_реш = 1/3·C_Vф·<υ_ф>·<l_ф>,

где C_Vф – теплоемкость единицы объема тела, связанная с тепловыми колебаниями атомов; <υ_ф> - средняя скорость фононов, близкая к скорости звука в теле; <l_ф> - средняя длина свободного пробега фононов между двумя последовательными актами рассеяния энергии, вызванными столкновениями фононов между собой или со статическими дефектами решетки.

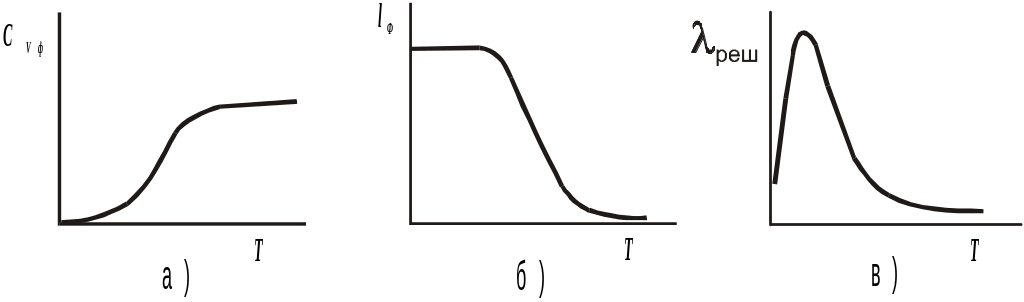
Рис. 1. Температурные зависимости С_Vф <l_ф>, _{реш для теплопроводности решетки}

Зависимость _реш от температуры (Т) (рис. 1в) определяется, в основном, температурным изменением величин С_Vф и <l_ф>. Скорость фононов <υ_ф> почти не изменяется, так как скорость звука слабо зависит от Т.

Влияние С_vф на величину _реш (рис. 1а,в) проявляется через зависимость концентрации фононов, переносящих энергию, от Т. При низких Т таких фононов мало, а, значит, мала переносимая ими суммарная энергия, что соответствует небольшим значениям С_vфи_реш. С повышением Т энергия отдельных фононов и их концентрация увеличиваются, при этом С_vф растет до некоторого постоянного значения. Это приводит к прекращению роста _{реш, что соответствует максимуму на кривой} (рис. 1в). Влияние <l_ф> на величину _реш с ростом Т (рис. 1б,в) обусловлено изменением частоты взаимных столкновений фононов. При низких Т концентрация фононов очень мала, вследствие чего они редко сталкиваются между собой, что соответствует максимальной <l_ф>, ограниченной поверхностями раздела, например, границами зерен и размерами тела. Повышение Т приводит к резкому росту концентрации фононов, в связи с чем их столкновения становятся более частыми. Это вызывает уменьшение <l_ф>, что является определяющим фактором уменьшения _реш.

Электронная теплопроводность _эл характерна для металлических материалов и во многом сходна с явлением электропроводности. В процессе переноса тепла электроны передают энергию решетке за счет взаимодействия с фононами. При рассмотрении электронной теплопроводности можно воспользоваться соотношением, похожим на соотношение для фононного газа:

_эл = 1/3·C_Vэл· υ_F ·<l_эл>,

где C_Vэл – теплоемкость электронного газа; υ_F –скорость электронов; <l_эл> – средняя длина свободного пробега электронов между столкновениями с фононами и статическими дефектами тела.

Зависимость _эл от температуры Т определяется, в основном, температурным изменением величины <l_эл> и C_Vэл.Скорость электронов υ_F почти не изменяется.

Для понимания влияния C_Vэл на _эл необходимо иметь ввиду, что электроны в электронном газе подчиняются принципу Паули: на одном энергетическом подуровне может находиться не более двух электронов (рис 2).

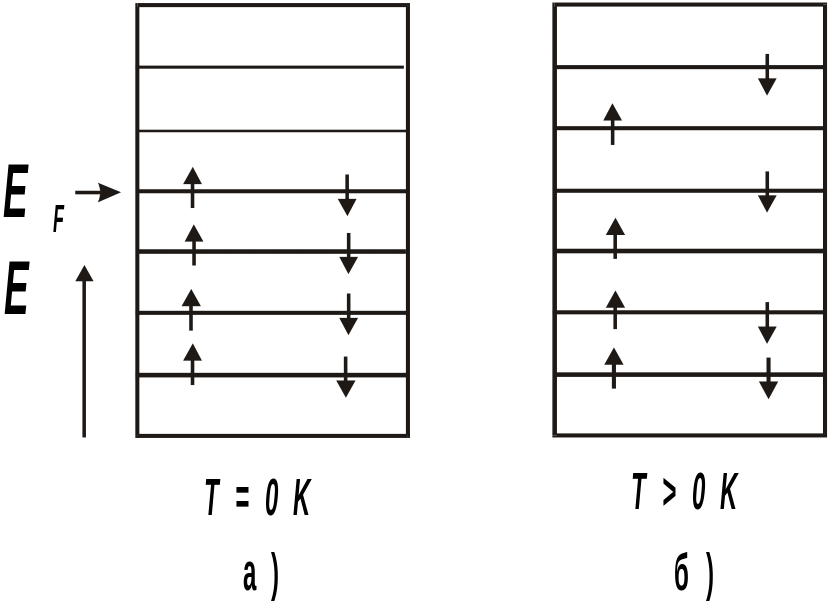
Рис. 2. Распределение электронов по энергиям в металле

Поглощение электроном энергии означает его переход на более высокие энергетические подуровни. Из этого следует, что поглощать тепловую энергию и участвовать в процессе ее переноса могут только электроны, имеющие возможность перейти на более высокие свободные энергетические подуровни, то есть уже находящиеся на самых высоких подуровнях. Такие электроны имеют большую и практически неизменную скорость υ_F. При низких температурах их концентрация очень мала по отношению к общей концентрации электронов, поэтому поглощаемая и переносимая ими суммарная энергия также невелика и, как следствие, мала C_Vэл и _эл (рис.3).

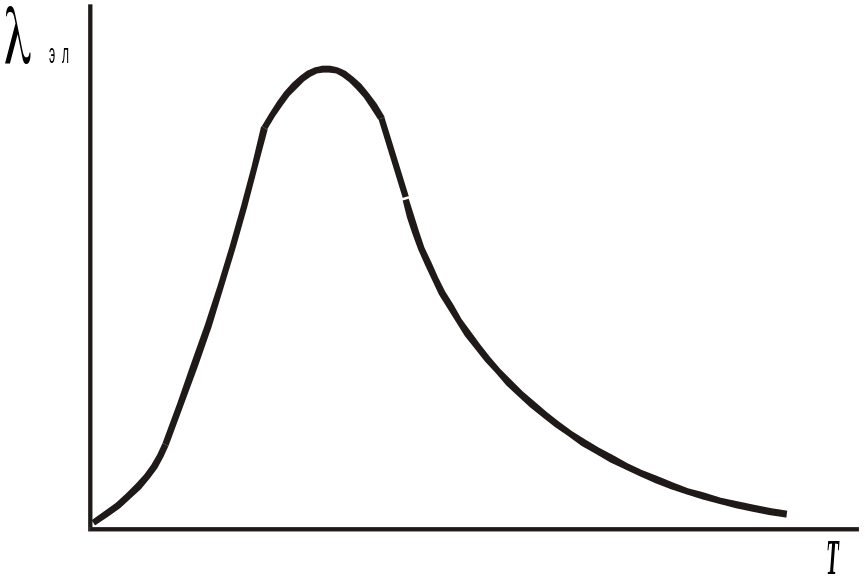
Рис. 3. Температурная зависимость _эл

Но с повышением Т концентрация электронов проводимости растет, несколько увеличивая C_Vэл и, соответственно, _эл металла.

С другой стороны при температурах близких к 0К невысока концентрация фононов, поэтому электрон-фононное взаимодействие маловероятно, и <l_эл> ограничена только примесями и дефектами решетки. Рост температуры приводит к увеличению числа фононов и электронов проводимости, вследствие чего <l_эл> начинает уменьшаться за счет более частых электрон-фононных столкновений, что способствует уменьшению _эл. Поэтому в области низких температур малая _эл объясняется низкой концентрацией электронов проводимости несмотря на большую <l_эл>. В области максимума _эл уже достаточно велика концентрация электронов проводимости и еще не слишком мала <l_эл>. В области высоких температур, несмотря на увеличение концентрации подвижных электронов, они имеют резко уменьшающуюся <l_эл>, что понижает результирующую _эл.

Между удельной электронной теплопроводностью _эл и удельной электрической проводимостью  чистых металлов выполняется соотношение:

_эл/ = L·T,

где L=2,45·10^-8 Вт·Ом / К^{2 -} число Лоренца.

Поскольку в диэлектриках концентрация электронов проводимости чрезвычайно мала, то теплопроводность диэлектриков обусловлена фононной теплопроводностью.

Теплопроводность металлов в общем случае складывается из теплопроводности, обеспеченной фононами и свободными электронами:

 = _реш + _эл

Однако в связи с тем, что υ_F значительно больше <υ_ф> электронная теплопроводность примерно в 100 раз превышает теплопроводность, обусловленную фононами, поэтому металлы проводят тепло лучше, чем диэлектрики. Фононной составляющей теплопроводности в данном случае можно пренебречь.

Зависимость от состава в сплавах твердых растворах и механических смесях имеет характер схожий с концентрационной зависимостью электропроводности. Для неупорядоченных твердых растворов зависимость теплопроводности имеет минимум в районе 50 % (атомных), так как при этом концентрация статических точечных искажений решетки, вызванных присутствием атомов разного вида, будет максимальной (рис.4) (см. «Удельное электрическое сопротивление сплавов – твердых растворов»).

При упорядочении твердых растворов происходит резкое увеличение . Для сплавов - механических смесей суммарная виличина  складывается из  отдельных составляющих с учетом их объемной доли и расположения относительно потока тепла. Однако, величина  в данном случае не превышает теплопроводность чистых компонентов (см. «Удельное электрическое сопротивление сплавов - механических смесей»). Заметное влияение на значение оказывает величина зерен поликристалла – чем больше размер зерен, тем выше Это следует принимать во внимание при выборе скоростей нагрева в процессе термоообработки и оценке прокаливаемости стали. 

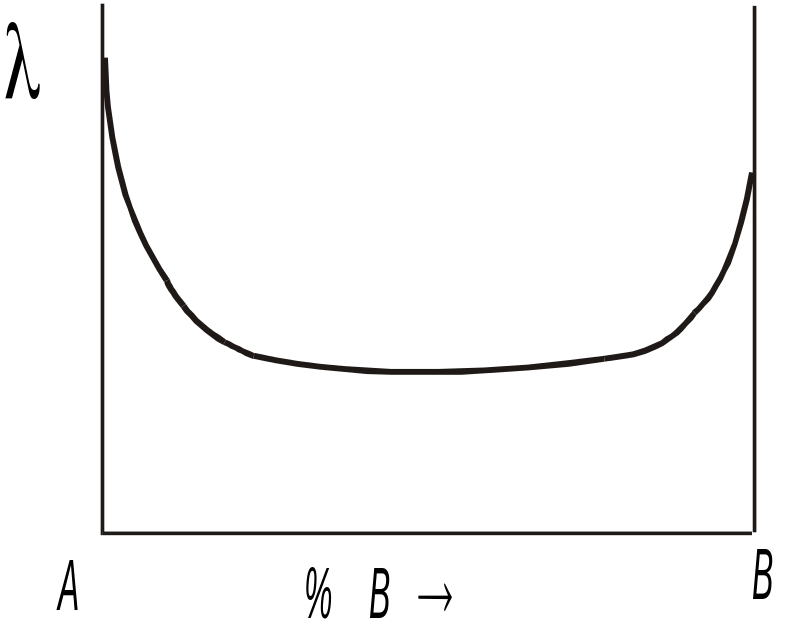
Рис. 4. Концентрационная зависимость теплопроводности для неупорядоченных твердых растворов

В данной работе для используется метод Кольрауша, основанный на измерении разницы температур между серединой и концами тонкого проволочного образца, нагреваемого электрическим током (рис. 5).

За счет продольного потока тепла, середина образца оказывается более нагретой, чем его концы, закрепленные на массивных медных токоподводах. Если разность потенциалов между концами образца равна U, а температура в середине и на концах Т_с и Т_о соответственно, то для образца, находящегося в вакууме, без учета потерь на излучение выполняется соотношение

Tс – T_o = T = U² / (8··_T), (1)

где _ коэффициент теплопроводности материала нагретого образца, удельное электрическое сопротивление.

Изменение средней температуры образца Т_ср по отношению к T_o. определяется по изменению его электрического сопротивления R с учетом известного табличного значения _ при 20С:

T_ср = (R_T – R₀) / (_·R₀₎, (2)

где T_ср- изменение средней температуры образца; R_T – сопротивление нагретого образца; R₀ – сопротивление при 20С; _ - температурный коэффициент удельного сопротивления.

Разница температур между серединой образца и его краями определяется из следующего равенства:

Т=2Т_ср (3)

Таким образом, измеряя сопротивление образца при нормальных условиях и в нагретом состоянии, а также ток I, протекающий в образце, зная его геометрические размеры, можно определить коэффициент теплопроводности

_ = U² /(8·_T·T) = I²·R_T² ·l₀ /(8·R_TS₀·T) = I²·R_T· l₀ /(8·S₀·T) =

I²·R_T·l₀ /(16·S₀·T_ср), Вт/(м·К), (4)

где l₀ - длина образца; S₀ – площадь сечения образца.

Полученные результаты должны быть проанализированы на основе представлений о физической природе теплопроводности металлических материалов.

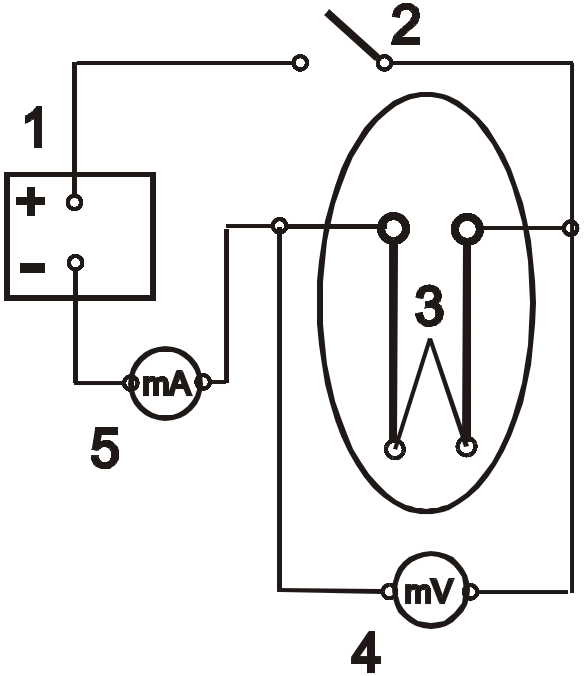
Рис. 5. Схема установки для определения теплопроводности