Лабораторная работа № 3 тепловые свойства материалов

Часть 1. Тепловое расширение сплавов – твердых растворов

Цель работы: на примере системы Cu-Ni исследовать зависимость теплового расширения сплавов – неограниченных твердых растворов замещения от их состава.

Содержание работы

Изменение размеров твердого тела в зависимости от температуры должно постоянно учитываться при проектировании технических устройств, так как нередко определяет их работоспособность. С другой стороны тепловое изменение размеров может быть использовано в измерительных устройствах и исполнительных механизмах. Поэтому знание закономерностей этого явления необходимо для оптимального выбора материалов.

Выясним физическую природу теплового расширения, анализируя закон взаимодействия частиц (атомов, ионов, молекул).

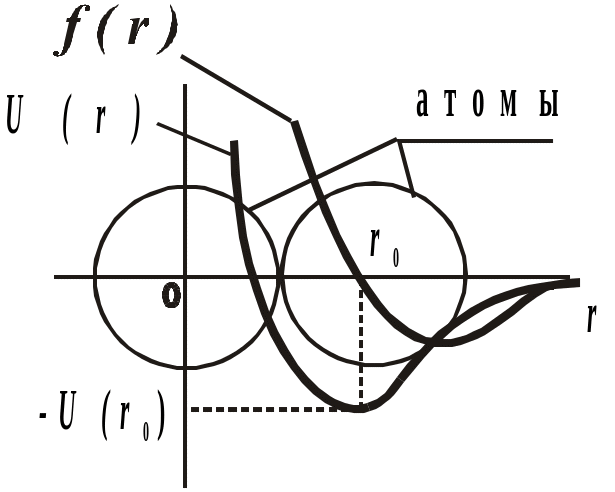
Рис. 1. Кривые межатомного взаимодействия; -U (r₀) - потенциальная энергия в положении равновесия r₀

Для двухатомной модели твердого тела (рис. 1) потенциальная энергия межатомного взаимодействия U(r) складывается из энергии, обусловленной действием сил притяжения и отталкивания атомов, что может быть представлено выражением:

U(r) = U(r)_пр + U(r)_отт = (-C/r^m) + (D/rⁿ),

здесь C и D константы; r – межатомное расстояние. Важно отметить, что из-за различной физической природы сил притяжения и отталкивания показатель степени m < n. Из условия m < n следует асимметрия закона взаимодействия.

Для удобства рассмотрения допустим, что атом, находящийся в начале системы координат неподвижен, а второй атом – подвижен и может совершать колебания около положения равновесия. По мере увеличения кинетической энергии W, вызванного повышением температуры Т тела, амплитуда колебаний подвижного атома будет увеличиваться. При этом его среднее положение (центр колебаний) смещается вправо по кривой ab (рис. 2), что и соответствует тепловому расширению.

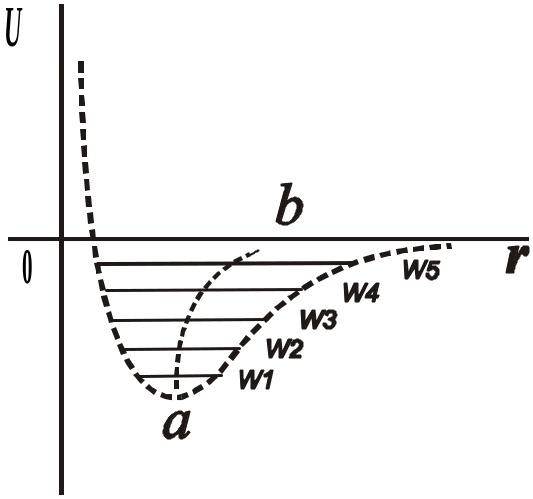
Рис. 2. Смещение центра колебаний атома с ростом кинетической энергии колебаний W.

Очевидно, что, чем больше энергия межатомной связи, равная /-U(r₀)/, тем выше температура плавления кристалла. Установлено также, что при нагреве до температуры плавления большинство металлических материалов увеличивают свой объем примерно на 7%. Это позволяет сделать следующий вывод: чем больше температура плавления материала, тем меньше тепловое расширение, приходящееся на один градус нагрева.

Количественной характеристикой теплового расширения тел является, как известно, температурный коэффициент линейного расширения

_L = L / (L₀·T),

здесь L - абсолютное удлинение при повышении температуры на величину T; L₀ - начальная длина образца. Величина _L является средней для данного температурного интервала T. Истинная (дифференциальная) величина коэффициента линейного расширения равна

_L =(dL / dT) 1/L₀.

Найдем связь между коэффициентом теплового расширения и параметрами межатомного взаимодействия. Если колебания атомов в рассматриваемой модели достаточно малы, то силу взаимодействия f (рис. 1) можно принять прямо пропорциональной смещению x из положения равновесия r₀

f = -·х,

где  – константа взаимодействия; смещение x = r – r₀

Данной линейной зависимости f от х соответствует параболический ход кривой потенциальной энергии U(r) (кривая cd на рис. 3). При этом изменение потенциальной энергии U(r) может быть выражено через смещение x:

U(r) = -U(r) - (-U(r₀)) = (1/2)· ·x²,

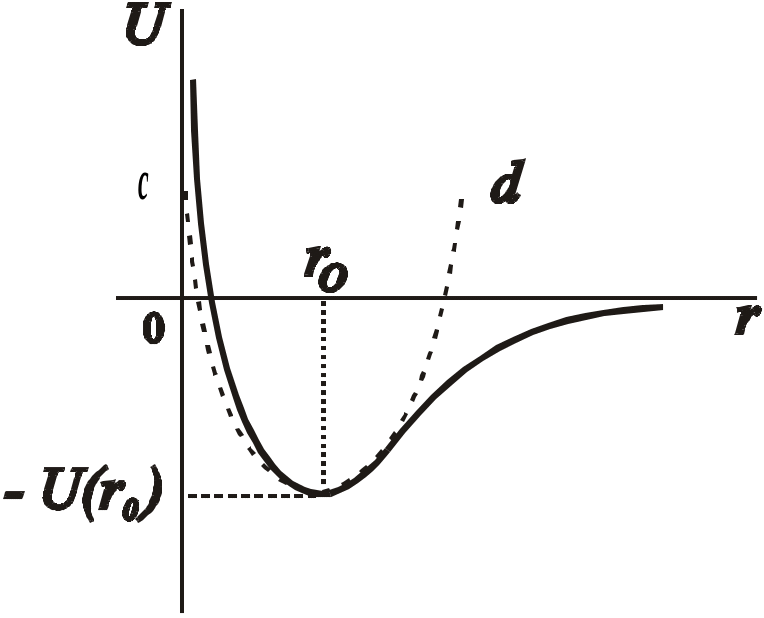
Рис.3 Симметричный и асимметричный характер колебаний атома

Очевидно, что в этом случае подвижным атомом совершаются гармонические, то есть симметричные колебания и среднее смещение относительно положения равновесия <x> =0, что соответствует отсутствию теплового расширения.

Однако, так как реальный закон взаимодействия асимметричен, то и колебания должны иметь асимметричный характер. Приблизительный учет асимметрии взаимодействия производится включением в выражение для U(r) дополнительного члена, содержащего нечетную степень х:

U(r) = (1/2··x² – 1/3··x³),

где  – константа взаимодействия.

Получим выражение для силы взаимодействия f с учетом асимметрии взаимодействия

f = - d(U(r))/dx = - ·x + ·x²,

Анализ выражения для f показывает, что при удалении атомов друг от друга из точки r₀ сила взаимодействия изменяется более плавно, чем при их сближении, что и отражает асимметрию взаимодействия. Поэтому при сближении атомов результирующим взаимодействием является резкое отталкивание и, как следствие, остановка атома на сближении – х. При удалении действует в основном плавное притяжение и остановка атома на удалении +х. Так как |+x| > |-x|, то атомы, по мере увеличения энергии ассиметричных колебаний, все больше удаляются друг от друга. Вследствие этого при Т >0K подвижный атом колеблется около центра колебаний, смещенного относительно r₀ на среднюю величину <x> >0. Полагая, что <f> =0, получим

<x> = (/)·<x²>.

Допустив, что тепловые колебания носят гармонический характер и учитывая, что средняя потенциальная энергия колебаний атомов U(r)=(1/2)··<x²> равна средней кинетической энергии колебаний W=(1/2)·k·T (k – постоянная Больцмана) получим

<x²> = (k·T) / 

В результате для средней величины смещения <х> реализуется известное приближение

<х> = ·k·T,

где = /² - коэффициент, учитывающий асимметричность (ангармоничность) колебаний атомов и жесткость связей.

Выражение для истинного коэффициента линейного расширения применительно к модели из двух атомов и к атомной цепочке, состоящей из атомов одного вида, можно записать

_L = (dx/dT)·1/r₀.

Учитывая выражение для <x> можно найти темп смещения атомов от положения равновесия в зависимости от температуры:

dx/dT = ·k,

тогда

_L = ·k·1/r_0.

Если цепочка состоит из атомов различного вида А и В, то выражения для _L можно преобразовать:

_L=((n_АA·_АA+n_АВ·_АВ+n_ВB·_ВB) / N)·k·1/<r₀>,

где n_AA, n_AB, n_BB – число соседств атомов АА, АВ, ВВ; N – общее число атомов в цепочке; <r₀> - среднее расстояние между атомами в цепочке.

Формула позволяет прогнозировать поведение _L в сплавах различного состава и строения. Например, если атомы сплава образуют неупорядоченный твердый раствор замещения, то в цепочке они располагаются случайным образом, тогда количество пар атомов n_АА, n_АB, n_BB, определяется вероятностью их встречи в цепочке

n_АА =1/2N_AZN_A/N=NC_A^2,

где Z - число соседей атомов в цепочке; C_A= N_A/N – концентрация атомов А; C_A² - вероятность встречи атомов А.

Аналогично можно показать:

n_BB=N·C_B^2,

n_АB=2N·C_А·C_B..

Путем подстановки получаем для неупорядоченного твердого раствора

_L = ((С_A²· _AA+ 2С_A · С_B· _AB+ С_B²· _BB)·k·1/<r₀>).

Можно также вывести зависимость _L в упорядоченных твердых растворах, механических смесях и сплавах, содержащих упорядоченную фазу (например, химическое соединение).

Константы _AA, _BB определяются значениями коэффициентов расширения компонентов сплавов и параметрами их кристаллических решеток. Значение _AB в случае неупорядоченных твердых растворов можно оценить, сопоставляя теоретические и экспериментальные концентрационные зависимости _{L .}

На величину _L мало влияет структурное состояние материала, наличие в нем дефектов кристаллической решетки, однако, _L зависит от направления в кристаллической решетке. Для поликристаллов _L может быть изотропным из-за хаотичной ориентации зерен.

В работе экспериментально определяется концентрационная зависимость коэффициента теплового расширения сплавов – твердых растворов системы Cu-Ni.

Полученные результаты должны быть проанализированы на основе физических представлений о влиянии состава и типа сплава на тепловое расширение.