1. Определение и задачи эконометрики. Место эконометрики в общественных науках

Эконометрика – это наука, кот. дает конкретное количественное выражение общим (качественным) взаимосвязям эк. явлений и процессов, обусловленным эк. теорией.

Эконометрика (сейчас) – наука о моделировании эк. явлений, позволяющем прогнозировать их развитие, выявлять и измерять определяющие факторы.

Эконометрика - это наука, изучающая количественные закономерности эк. явлений и процессов, с помощью статистических методов и моделей.

Базовые компоненты:

1. Эк. теория. Разрабатываются концепции развития изучаемых процессов;

2. Статистика. Процессы выражаются в статистических показателях;

3. Математика. Построение модели изучаемых процессов, оценка их параметры, соответствие реальным данным, прогнозирование развития изучаемого явления.

Главное назначение Э. – модельное описание конкретных количественных взаимосвязей, существующих между анализируемыми показателями.

Задачи разграничиваются по трем параметрам:

1. По конечным прикладным целям (прогноз соц. и эк. показателей; имитация различных возможных сценариев соц.-эк. развития анализируемой системы);

2. По уровню иерархии анализируемой системы (построение э. модели на разных уровнях: страна, регион, отрасль, домохозяйство, фирма);

3. По профилю анализируемой системы (исследование проблем рынка (спрос, предложение, инвестиц. политика)).

Предмет эконометрики – экономика в количественном аспекте.

Объект изучения эконометрики – связи, существующие в эк. жизни.

Главный инструмент эконометрики – эконометрическая модель.

Место в науках: Входит в семейство дисциплин, посвященных измерениям и применению статистических методов в различных областях науки и практики. Отдельно социометрия — статистические методы анализа взаимоотношений в малых группах, статистический анализ в социологии.

2. История эконометрических исследований

Предпосылки возникновения эконометрики и этапы развития:

1. Разработка количественных методов в экономических исследованиях;

2. Накопление учетно-статистических данных;

3. Создание современной микро - и макроэкономики.

Развитие:

1. Зарождение количественного подхода к эк. - 2п. 17в., школа политических арифметиков (Петти и Граунт) - особенность говорить об эк. на языке мер, весов и чисел.

2. Работы Адольфа Кетле (1786-1874). «Теория среднего человека» и "Соц. физика". Включил в методы познания кривые распределения, средние величины и отклонения от средних; важность статистики в раскрытии соц. законов.

3. Выявление закономерности формирования потребления: пропорциональность отношения полных расходов и расходов на питание к приросту доходов домохозяйства (Энгель, Швабе, Слуцкий, Боули).

4. Анализ закономерности распределения доходов Парето (кривая Парето),

где У – число лиц, получающих доход больше Х: y = a/(x-a)^a

5. Работы на основе временных рядов – циклическая экономика (динамика эк. явлений), например Функция Кобба – Дугласа: Р = а * L^b1 * K^b2 * e, Р - объем производства; L - численность занятых; К - объем капитала; а, b1, b2- параметры; e - случайная компонента.

6. 30-е гг. – макроэк. моделирование (по теории Кейнса) -15 моделей, 5 тождеств, 40 эк. показателей.

3. Методология эконометрического моделирования

Главный инструмент эконометрики – эконометрическая модель, параметры которой оцениваются с помощью методов математической статистики.

Виды моделей, используемых в эконометрическом моделировании:

1. Регрессионные модели с одним уравнением (лин., лелин., парные, множ. регрессия);

2. Системы одновременных уравнений (взаимосвязанных – 1 уравнение и 1 баланс. тождество);

3. Модели временных рядов (трендов, сезонности, взаимосвязи по временным рядам, авторегрессии, с распред. ладом).

1. Статические и динамические – по характеру исп-х данных (1 – основаны на одновременных данных по совокупности объектов, 2 – на временных рядах). Промежуточные - модели панельных данных, основанные на данных по одной и той же совокупности за ряд лет;

2. Комплексные и не комплексные (1 отличаются тем, что отражают связи между макроэк. показателями на всех стадиях процесса воспроизводства)

3. Аналитические, имитационные и прогностические (по целям применения).

Этапы построение э. модели:

1. Теоретическое описание рассматриваемого эк. процесса с отражением существующих тенденций, постановка проблемы.

2. Сбор данных, анализ их качества.

3. Спецификация модели – выбор формы модели с подбором соотв. экзогенных (внешние) и эндогенных (внутренние) переменных.

4. Идентификация модели – выявление условий корректного оценивания параметров модели на основе соотношения количества переменных и связей между ними.

5. Оценка параметров модели.

6. Верификация модели, то есть проверка достоверности модели.

4. Выбор типа математической функции при построении уравнения регрессии

Регрессный анализ заключается в определении аналитического выражения связи между явлениями, в котором изменение одной величины (зависимой) обусловлено влиянием одной или нескольких независимых величин.

Условия применения корреляционно-регрессионного метода:

1. Наличие данных по достаточно большой совокупности;

2. Однородность совокупности;

3. Необходимость подчинения распределения совокупности по факторному и результативному признакам нормальному закону распределения.

Задачи корреляционно-регрессионного метода:

1. Измерение параметров уравнения, выражающего связь между признаками. Решается оценкой параметров уравнения регрессии.

2. Измерение тесноты связи между признаками. Решается оценкой показателей корреляции.

Виды функций, наиболее часто используемые в эконометрическом моделировании:

1. Линейная y = a + bx

2. Гипербола y = a + b/x – 1/x = z; a + bz

3. Парабола второго порядка y = a + bx + cx² – x² = z; y = a + bx + cz

4. Степенная функция y = ax^b – lgy = lga + b*lgx

5. Показательная функция y = ab^x – lny = lna + x*lnb

6. Экспонента y = e^{a + bx} – lny = a + bx

7. Обратная модель y = 1/(a + bx)

8. Логарифмическая y = a + b*lnx

!!! Если ф. нелинейная, то для оценки параметров ее нужно привести к линейному виду (сбоку).

Методы выбора функции:

1. Аналитический метод (теоретический анализ взаимосвязи между признаками);

2. Графический метод (строится поле корреляции - выводы);

3. Экспериментальный метод (строим разные функции - выбор).

5. Оценка параметров уравнения парной регрессии

Эконометрическое оценивание моделей включает два основных этапа:

1. Теоретический. Считается, что определена генеральная совокупность. Зная ее статистические свойства, м. теоретически определить параметры модели.

2. Эмпирический. Используются выборочные данные. Можно оценить, но нельзя точно определить значения параметров модели, т.к. они являются случайными величинами.

Параметры - характеристики генеральной совокупности.

Оценки - характеристики выборочной совокупности.

Оценка генеральных параметров может быть получена двумя методами:

а) МНК – используется чаще;

б) методом максимального правдоподобия.

Требования к оценкам (свойства):

1. Несмещенность. В среднем оценка соответствует параметру при любом объеме выборки.

2. Эффективность. Несмещенная оценка эффективна, если она имеет мин. дисперсию по сравнению с другими выборочными оценками. Та из оценок, которая имеет меньшую дисперсию, является более эффективной.

3. Состоятельность. Оценка состоятельна, если при увеличении объема выборки она стремится к оцениваемому параметру. Т.е. х_ср не отличается от µ, когда n → ∞.

Для оценки параметров лин. ф., используется МНК: Σ (у – у_{с крыш})² → min. Позволяет получить оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака от теоретических минимальна.

Для линейных и нелинейных уравнений, привод. к лин., решается система относительно а и b: Σу = na + bΣx; Σyx = aΣx + bΣx² – система норм. ур-ий.

Тогда можно вывести формулы для нахождения параметров системы:

b = (yх_ср - х_ср * y_ср) / (x²_ср – x_ср²); а = y_ср - b х_ср.

а - свободный член уравнения регрессии; экономически не интерпретируется.

b - абсолютный показатель силы связи (в лин. ур-ии). Наклон линии регрессии или коэффициент регрессии. Мера зависимости у от х.

Условия применения МНК:

1. Модель регрессии должна быть линейной по параметрам.

2. x – не стохастическая переменная (не случайная).

3. Значения ошибки (остатка) - случайные. Их изменение не образует опред. модели.

4. Число наблюдений д.б. больше числа оцениваемых параметров (в 5-6 раз).

5. Значения переменной x не должны быть одинаковыми.

6. Изучаемая совокупность должна быть однородной.

7. Отсутствие взаимосвязи между фактором x и остатком.

8. Модель регрессии должна быть корректно специфицирована.

9. В модели не должно наблюдаться тесной взаимосвязи между факторами (для множ. регрессии).

6. Абсолютные и относительные показатели силы связи в уравнениях парной регрессии

Абсолютные – показывают, на сколько единиц в среднем меняется результативный признак при изменении факторного признака на одну единицу (в лин. ур-ии b - абсолютный показатель силы связи).

Относительные (коэфф. эластичности) - показывают, на сколько % в среднем меняется результативный признак при изменении факторного признака на 1%.

Коэффициент эластичности: Э = f’(x) * x/y.

Ф-ия: Абс: Отн:

1. Линейная y = a + bx: b_ср b*x_ср/ у_ср

2. Гипербола y = a + b/x: -b/x² -b/ax + b

3. Парабола второго порядка y = a + bx + cx² : b + 2cx (b + 2cx)x/(a+bx+cx²)

4. Степенная функция y = ax^b : abx^b-1 b_ср

5. Показательная функция y = ab^x : ab^x lnb x*lnb

7. Показатели тесноты связи в моделях парной регрессии

Насколько близко фактические значения показателя расположены к линии регрессии. Чем ближе, тем теснее.

Теснота связи – характеризует, насколько фактор или факторы, включенные в уравнение регрессии, объясняют изменение результата.

I. Коэфф. детерминации – обобщенный показатель оценки построенного уровня регрессии; показывает долю вариации (дисперсии) результативного признака, объясняемую регрессией, в общей вариации результата.

r² = SS_R / SS_T = 1 - SS_E / SS_T.

r² = [0; 1]. 0 – связи нет, 1 – связь функциональная.

В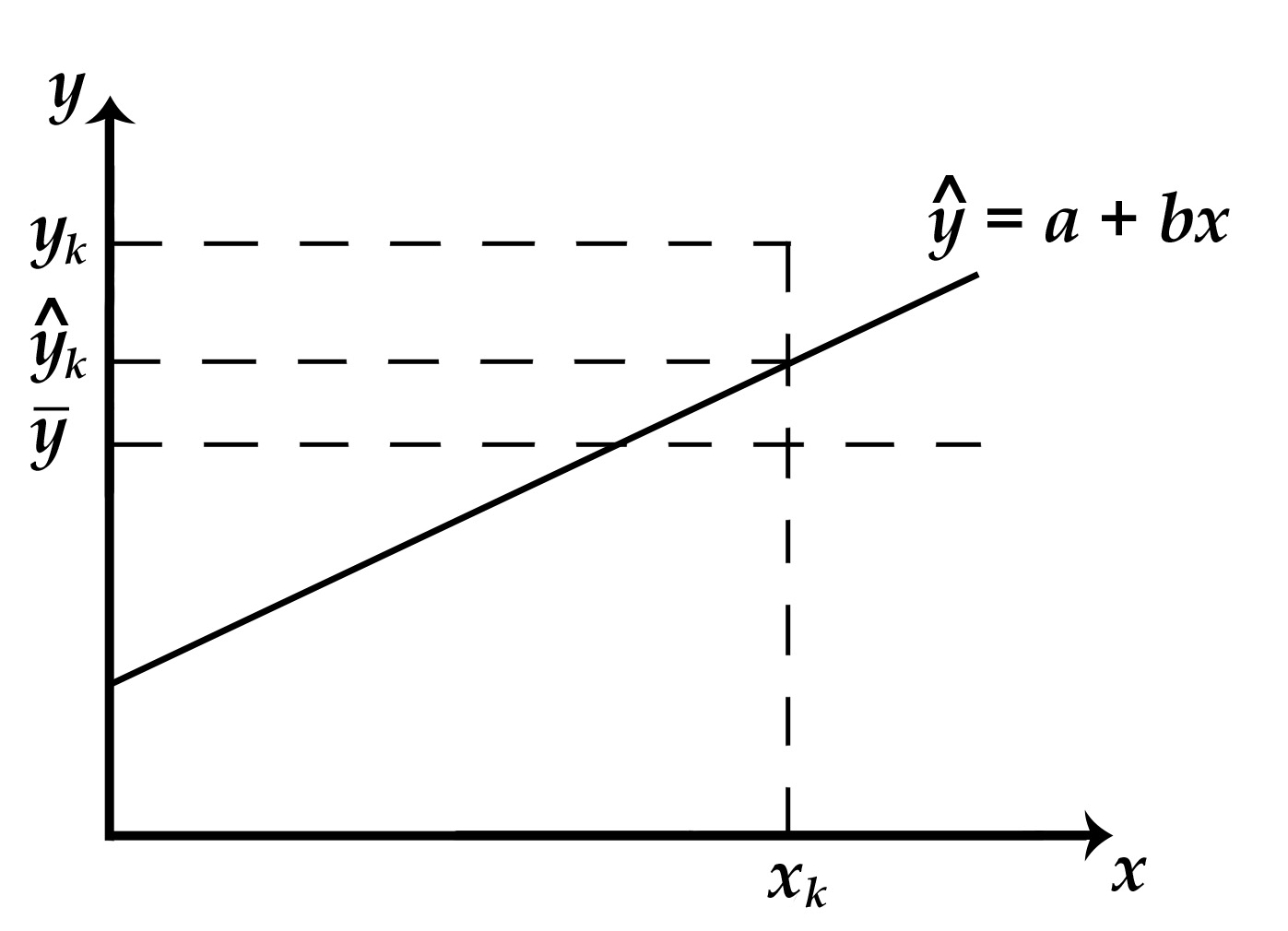 его основе – правило сложения дисперсий.

Если подставим в y_{с крыш} вместо х у_к.,

то получим, что фактич. значение =

теор. значению.

1. (у_к – у_ср) – общее отклонение за счет всех факторов;

2. (у_к –у_{к с крыш}) – ошибка (остаток); отклонение за счет прочих неучтенных факторов;

3. (у_{к с крыш} – у_ср) – отклонение за счет учтенных факторов.

Если рассмотреть множество точек, то:

Σ(у – у_ср)² = Σ(у – у_{с крыш})² + Σ(у_{с крыш} – у_ср)²

SS_T = SS_R + SS_E

1. (у – у_ср) ² = SS_T - общая сумма квадратов отклонений;

2. (у – у_{с крыш}) ² = SS_R - факторная сумма квадратов отклонений;

3. (у_{с крыш} – у_ср) ² = SS_E - остаточная сумма квадратов отклонений.

Если разделить SS на n (количество единиц совокупности), то:

δ_T² = δ_R² + δ_E²

II. Индекс корреляции.

Корень из r² = ŋ = корень из (SS_R / SS_T)= корень из (1 - SS_E / SS_T); ŋ = [0; 1] – чем ближе к 1, тем теснее связь.

!!! При измерении лин. связи индекс корреляции совпадает с коэфф. корреляции.

III. Коэфф. корреляции.

r = b * δ_х / δ_у = ((ух)_ср - х_сру_ср ) / (δ_х δ_у) – только для лин. регрессии.

r = [-1; 1]. Чем ближе к 1 по модулю, тем теснее связь.

Свойства r:

- r - стандартизованный коэффициент регрессии;

- r сравним для признаков с разными единицами измерения;

- если связи между х и у нет, то r = 0; НО если r = 0, то нет только линейной связи;

- r_ху = r_ух.

Шкала значения коэфф. корреляции:

1. До 0,3 связь слабая 2. 0,3-0,5 связь умеренная

3. 0,5-0,7 связь заметная 4. 0,7-0,9 связь высокая

5. 0,9-1,0 связь весьма высокая, близкая к функциональной.

Вывод: на r² % вариация признака зависит от включенного в модель фактора (- ов), остальные (1 - r²)% - зависит от прочих неучтенных факторов.

8. Статистический анализ достоверности модели парной регрессии

Значение коэфф. детерминации r² может отражать истинную зависимость, а может – стечение обстоятельств, т.к. при построении уравнения используются выборочные данные. Поэтому необходимо определить, насколько выборочные показатели (оценки) достоверны, значимы. Для этого используют вероятностные оценки стат. гипотез.

Статистическая гипотеза (Н) - предположение о свойстве генеральной совокупности, которое можно проверить, опираясь на данные выборки.

Этапы проверки статистических гипотез:

1. формулируется задача исследования в виде стат. гипотезы;

2. выбирается статистическая характеристика гипотезы;

3. выдвигаются испытуемая и альтернативная Н₀ и Н₁;

4. определяется ОДЗ, критическая область и критическое значение статистического критерия;

5. вычисляется фактическое значение статистического критерия;

6. испытуемая Н₁ проверяется на основе сравнения значений фактического и критического критерия, и в зависимости от результатов проверки Н₁ либо отклоняется, либо принимается.

Критическая область – область, попадание значения статистического критерия в которую приводит к отклонению Н₀ . Вероятность попадания значения критерия в эту область равна уровню значимости (1 минус доверительная вероятность).

ОДЗ - область, попадание значения статистического критерия в которую приводит к принятию Н₀.

Статистическая оценка достоверности регрессионной модели:

1. выдвигается H₀: r² в генеральной совокупности = 0;

2. выдвигается H₁: r² в генеральной совокупности не = 0;

3. определяется ОДЗ или уровень значимости;

4. рассчитывается критерий Фишера F (n – число единиц совокупности, m – число факторов):

F = MS_R / MS_E = (Σ(y _{с крыш} – y_ср)² / m) / (Σ(y– y _{с крыш})² / (n-m-1))

F = r²/(1-r²) * (n-m-1)/m = r²/ (1-r²) * (n-²);

5. определяется табличное значение критерия Фишера F_табл;

6. фактическое значение сравнивается с табличным.

а. Если F>Fтабл., то гипотеза о случайной природе оцениваемых характеристик отклоняется и признается статистическая значимость и надежность.

б. Если F<Fтабл., то гипотеза о случ… не отклоняется и признается статистическая незначимость, ненадежность уравнения регрессии.

Число степеней свободы (df) - число свободно варьируемых переменных.

df_T = df_R + df_E; n-1 = m + (n – m – 1).

При расчете фактической суммы квадратных отклонений ((у – у_{с крыш}) ² = SS_R) используются теоретические значения результативного признака (у_{с крыш}), определенного по линии регрессии (у_{с крыш} = a + bx). Т.к. объясненная (факторная) сумма квадратов зависит только от 1-ой константы, то данная модель имеет 1-у степень свободы.

Если разделить сумму квадратов на число степеней свободы, можно получить дисперсии на 1-у степень свободы (MS):

MS_R = SS_R/df_R = Σ(y _{с крыш} – y_ср)² / m

MS_Е = SS_Е/df_Е = Σ(y– y _{с крыш})² / (n-m-1)

9. Таблица дисперсионного анализа (назначение, построение)

Все показатели м. оформить в виде таблицы дисперсионного анализа ANOVA.

Источник вариации:	df	SS	MS	F
- регрессия	m	SSR	MSR	F
- остаток	n-m-1	SSE	MSE	–
- итого	n-1	SST	–	–

df – кол-во степеней свободы; MS = SS/df – дисперсия на 1 степень свободы; SS - сумма квадратов отклонений (общ., факт., остат.); F = MS_R/MS_E – критерий Фишера.

10. Оценка значимости параметров уравнения парной регрессии

Оценка значимости коэффициентов регрессии:

1. Выдвигается Н₀: коэффициент регрессии b в генеральной совокупности равен 0;

2. Выдвигается Н₁: коэффициент регрессии b в генеральной совокупности не равен 0;

3. Определяется уровень значимости α;

4. Определяется критическое значение критерия Стьюдента (S_eb – станд. ошибка b; b – коэфф. регрессии, абс. показатель силы связи (в лин. ур-ии), мера зависимости у от х):

t = b/S_eb

S_eb = корень из (MS_E / Σ(x-x_ср)²) = корень из (Σ(у-у _{с крыш})²/(n-2))/Σ(x-x_ср)²

а. t > t_табл., то Н₀ отклоняется, то есть параметр b не случайно отличается от нуля, сформировался под влиянием систематически действующего фактора.

б. t < t_табл., то Н₀ не отклоняется, и признается случайная природа формирования b.

Можно проверить достоверность а (свободный член уравнения регрессии; экономически не интерпретируется):

S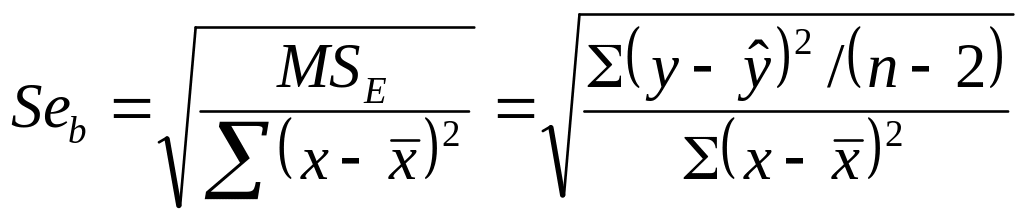 _eа = корень из (Σ(у-у _{с крыш})²/(n-2)) * Σx²/(n* Σ(х- x_ср)²)

11. Интервальная оценка параметров уравнения парной регрессии

Критическое значение критерия Стьюдента (S_eb – станд. ошибка b; b – коэфф. регрессии, абс. показатель силы связи (в лин. ур-ии), мера зависимости у от х):

t = b/S_eb

S_eb = корень из (MS_E / Σ(x-x_ср)²) = корень из (Σ(у-у _{с крыш})²/(n-2))/Σ(x-x_ср)²

∆_b – предельная ошибка.

∆_b = +– t_табл * S_eb

b - ∆_b <= b <= b + ∆_b

b – t_табл * S_eb <= b <= b + t_табл * S_eb

Вывод: с вероятностью α (0,95) можно утверждать, что параметр b генеральной совокупности находится в пределах от … и до… .

12. Нелинейная регрессия (линеаризация, оценка параметров)

Регрессный анализ заключается в определении аналитического выражения связи между явлениями, в котором изменение одной величины (зависимой) обусловлено влиянием одной или нескольких независимых величин.

Условия применения корреляционно-регрессионного метода:

1. Наличие данных по достаточно большой совокупности;

2. Однородность совокупности;

3. Необходимость подчинения распределения совокупности по факторному и результативному признакам нормальному закону распределения.

Задачи корреляционно-регрессионного метода:

1. Измерение параметров уравнения, выражающего связь между признаками. Решается оценкой параметров уравнения регрессии.

2. Измерение тесноты связи между признаками. Решается оценкой показателей корреляции.

Виды функций, наиболее часто используемые в эконометрическом моделировании:

1. Линейная y = a + bx

2. Гипербола y = a + b/x – 1/x = z; a + bz

3. Парабола второго порядка y = a + bx + cx² – x² = z; y = a + bx + cz

4. Степенная функция y = ax^b – lgy = lga + b*lgx

5. Показательная функция y = ab^x – lny = lna + x*lnb

6. Экспонента y = e^{a + bx} – lny = a + bx

!!! Если ф. нелинейная, то для оценки параметров ее нужно привести к линейному виду – линеаризация (сбоку).

Показатели:

1. Индекс корреляции:

R = корень из (1 - δ_E / δ_T) = корень из (1 - Σ(у-у _{с крыш})²/Σ(x-x_ср)²)

δ_E = Σ(у-у _{с крыш})² / n - остаточная дисперсия; δ_T = Σ(x-x_ср)² / n - общая дисперсия.

2. Оценка значимости коэфф. корреляции (R²):

F = MS_R / MS_E = (Σ(y _{с крыш} – y_ср)² / m) / (Σ(y– y _{с крыш})² / (n-m-1))

F = R²/(1-R²) * (n-m-1)/m = R²/ (1-R²) * (n-2);

а. Если F>Fтабл., то гипотеза о случайной природе оцениваемых характеристик отклоняется и признается статистическая значимость и надежность.

б. Если F<Fтабл., то гипотеза о случ… не отклоняется и признается статистическая незначимость, ненадежность уравнения регрессии.

!!! Все показатели м. оформить в виде таблицы дисперсионного анализа ANOVA.

Источник вариации:	df	SS	MS	F
- регрессия	m	SSR	MSR	F
- остаток	n-m-1	SSE	MSE	–
- итого	n-1	SST	–	–

df – кол-во степеней свободы; MS = SS/df – дисперсия на 1 степень свободы; SS - сумма квадратов отклонений (общ., факт., остат.); F = MS_R/MS_E – критерий Фишера.

3. Оценка значимости коэфф. регрессии (b):

t = (R² – r²) / m_|R-r|

m_|R-r| - ошибка разности между R² и r² .

m_|R-r| = 2 * корень из (((R² – r²) - (R² – r²) ² * (2 - (R² + r²)) / n)

а. t > t_табл., то различия между рассм. показателями корреляции существенны и замена нелинейной регрессии уравнением линейной невозможна.

б. t < 2, различия несущественны и возможно применение линейной регрессии.

13. Средняя ошибка аппроксимации

Оценку качества (достоверности) модели можно произвести не только с помощью постановки гипотезы о случайной природе оцениваемых характеристик (Н), критерия Фишера (F) и дисперсии на 1-у степень свободы (MS), но и с помощью нахождения ошибки аппроксимации .

Ошибка аппроксимации (А) – ошибка или остаток.

у – у_{с крыш} = ε

Можно рассчитать А по каждому наблюдению в относительном виде:

А = (Σ |(у-у _{с крыш}) / у| * 100%) / n

Расчет м. оформить в таблице:

№	y	x	у с крыш	у-у с крыш	|(у-у с крыш) / у| * 100%
1	10,57	1	21,48	-10,91	103,22
2	17,50	3	22,29	-4,79	27,37
…	…	…	…	…	…
Итого:	-	-	-	-	197,15

Если n = 8, то А = 197,15 / 8 = 24,64 %

Если А<10% - норма.

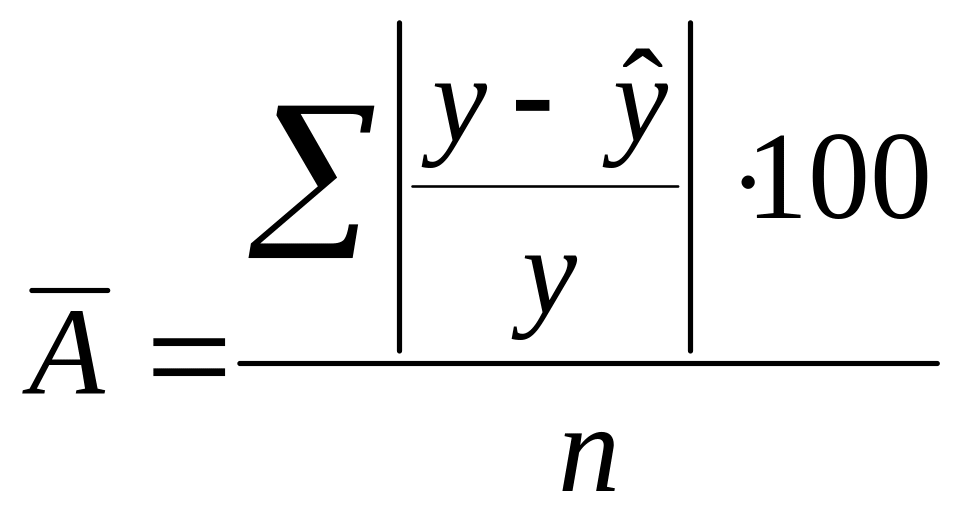
14. Использование модели парной регрессии для прогнозирования

Виды прогнозирования:

1. Точечный прогноз. Осуществляется путем постановки в найденное уравнение регрессии прогнозных значений х_р:

y _{с крыш р} = a + bх_р

Нужно учесть ошибку местоположения регрессии и ошибку каждого конкретного значения.

2. Интервальный прогноз.

а. Определяется средняя ошибка прогнозного значения у:

S_{e(y с крыш р)} = корень из (MS_E (1 + 1/n + Σ (х_р-x_ср)² / Σ (х - x_ср)²)

б. Строится доверительный интервал прогноза:

у_{с крыш р} – t_табл * S_{e(y с крыш р)} <= у_{с крыш р} <= у_{с крыш р} + t_табл * S_{e(y с крыш р)}

в. Вывод: с вероятностью α (0,95) можно утверждать, что прогнозное значение параметра находится в пределах от … и до… .

Если ф. нелинейная, то необходимо ее привести к линейному виду, а затем произвести прогноз.

15. Визуальный анализ остатков

Свойства остатков:

1. Отсутствие связи между остатками и факторной переменной.

2. Отсутствие связи между остатками и предсказанными значениями (у_{с крыш}).

3. Математическое ожидание остатков = 0; но в выборке Σ (у-у _{с крыш}) = 0.

4. Остатки имеют постоянную дисперсию. Дисперсия остатков = 1. Постоянство дисперсии остатков называют гомоскедастичностью остатков. Если же дисперсия остатков непостоянна, то имеет место гетероскедастичность остатков.

5. Остатки не коррелированны (не связаны) между собой.

6. Остатки д.б. распределены по нормальному закону распределения

Анализ остатков – разными методами. Один из них – визуальный анализ остатков.

16. Смысл и значение множественной регрессии в эконометрических исследованиях. Выбор формы уравнения множественной регрессии

Цель МР – построение модели с несколькими факторами у = f (х₁,х₂,…х_n), определив при этом их влияние в отдельности и в совокупности на результат.

Наиболее часто используются следующие функции:

1. линейная y = a + b₁x₁ +b₂x₂ + … ;

2. степенная y = ax₁^b1x₂^b2… ;

3. показательная y = ab₁^x1b₂^x2… ;

4. экспонета y = e^{a + b1x1 + b2x2 + …} ;

5. гипербола y = 1 / (a + b₁x₁ +b₂x₂ + …).

Если ф. нелинейная – линеаризация.

Методы выбора функции:

1. Аналитический метод (теоретический анализ взаимосвязи между признаками);

2. Экспериментальный метод (строим разные функции - выбор).

Графический метод (строится поле корреляции - выводы) – не используем.

17. Отбор факторов в уравнение множественной регрессии

Цель МР – построение модели с несколькими факторами у = f (х₁,х₂,…х_n), определив при этом их влияние в отдельности и в совокупности на результат.

При отборе факторов в уравнение МР необходимо соблюдать условия:

1. нужно включать только существенные факторы, непосредственно формирующее результат;

2. факторы должны быть количественно измерены;

3. факторы не должны находиться в тесной взаимосвязи друг с другом (значение коэффициента корреляции между факторами, входящими в модель должно быть менее 0,7; если больше, то такие параметры неинтерпретируемые).

Отбор факторов основан на 2 этапах:

1. теоретическом анализе взаимосвязи результата с кругом факторов;

2. количественном анализе (на основе матрицы парных коэффициентов корреляции, матрицы частных коэффициентов корреляции, с помощью стандартизованных коэффициентов регрессии, на основе F, t-критериев).

Отбор факторов:

1. метод последовательного включения факторов;

2. метод последовательного исключения факторов.

Т.е. оставляем тот фактор из 2 очень связанных, который с остальными менее связан. Убирает тот, что наоборот.

18. Оценка параметров уравнения множественной регрессии

Эконометрическое оценивание моделей включает два основных этапа:

1. Теоретический. Считается, что определена генеральная совокупность. Зная ее статистические свойства, м. теоретически определить параметры модели.

2. Эмпирический. Используются выборочные данные. Можно оценить, но нельзя точно определить значения параметров модели, т.к. они являются случайными величинами.

Параметры - характеристики генеральной совокупности. Оценки - характеристики выборочной совокупности.

Требования к оценкам (свойства):

1. Несмещенность. В среднем оценка соответствует параметру при любом объеме выборки.

2. Эффективность. Несмещенная оценка эффективна, если она имеет мин. дисперсию по сравнению с другими выборочными оценками. Та из оценок, которая имеет меньшую дисперсию, является более эффективной.

3. Состоятельность. Оценка состоятельна, если при увеличении объема выборки она стремится к оцениваемому параметру. Т.е. х_ср не отличается от µ, когда n → ∞.

Для оценки параметров уравнения множественной регрессии применяют МНК. Нелинейные ф. приводятся к линейному виду по параметрам.

Функция: y = a + b₁x₁ +b₂x₂ и система:

Σy = na + b₁ Σx₁ +b₂ Σx₂

Σyx₁ = a Σx₁ + b₁Σx₁² +b₂ Σx₁x₂

Σyx₂ = a Σx₂ + b₁Σ x₁x₂ +b₂ Σ x₂²

Система решается методами:

Подстановка: a = y_ср – b₁x_1ср – b₂x_2ср

b₁ = ((r_yx1 – r_yx2 * r_x1x2) / (1 – r²_x1x2)) * δ_y/δ_x1

b₂ = ((r_yx2 – r_yx1 * r_x1x2) / (1 – r²_x1x2)) * δ_y/δ_x2

где ß₁ = (r_yx1 – r_yx2 * r_x1x2) / (1 – r²_x1x2); ß₂ = (r_yx2 – r_yx1 * r_x1x2) / (1 – r²_x1x2).

Определитель:

1. Рассчитываем определитель системы ∆ (2,3,4) и частные определители ∆а (1,3,4), ∆b₁(2,1,4), ∆b₂(2,3,1).

2. Рассчитываем параметры а =∆а/∆; b1 =∆ b₁/∆; b2 =∆ b₂/∆.

3. Записываем уравнение y_{с крыш} = a + b₁x₁ +b₂x₂

b₁ и b₂ - абсолютные показатели силы связи.

19. Построение уравнения регрессии в стандартизованном масштабе

y = a + b₁x₁ +b₂x₂

Можно определить параметры системы с помощью построения уравнения в стандартизованном масштабе на основе матрицы парных коэффициентов.

t_y = ß₁t_x1 + ß₂t_x2 + … +ε

- t_xi, t_y - стандартизованные переменные, для которых среднее значение равно нулю: t_yср = t_xiср = 0.

t_y = (y - y_ср)/δ_y; t_xi = (x_i – x_iср)/δ_xi; t_ср = 0; δ_t = 1.

- ß – стандартизованные коэфф. регрессии.

Для оценки параметров уравнения множественной регрессии в стандартизованном масштабе применяют МНК. Нелинейные ф. приводятся к линейному виду по параметрам. Мы получили систему нормальных уравнений:

r_xy1 = ß₁ + ß₂ * r_x2x1 + ß₃ * r_x3x1 + …

r_xy2 = ß₁ * r_x1x2 + ß₂ + ß₃ * r_x3x2 + …

r_xy3 = ß₁ * r_x1x3 + ß₂ * r_x2x3 + ß₃ + …

Решим систему методом определителя:

1. Рассчитываем определитель системы ∆ (2,3,4) и частные определители ∆а (1,3,4), ∆b₁(2,1,4), ∆b₂(2,3,1).

2. Рассчитываем параметры – стандартизованные коэфф. регрессии ß₁ = ∆а/∆; ß₂ =∆ b₁/∆; ß₃ =∆ b₂/∆.

!!! Вывод: Стандартизованные коэфф. регрессии (ß-коэфф.) показывают, на сколько сигм (δ) изменится в среднем результат, если соответствующий фактор х_i изменится на 1 сигму (δ) при неизменном среднем уровне других факторов.

!!! Преимущество стандартизованных коэфф. над коэфф. чистой регрессии: Т.к. все переменные – центрированы и нормированы, то стандартизованные коэфф. ß_i сравнимы между собой. Сравнивая их, можно ранжировать факторы по силе их воздействия на результат.

20. Абсолютные и относительные показатели силы связи в модели множественной регрессии

Абсолютные - показывают, на сколько единиц в среднем изменяется результативный признак при изменении рассматриваемого факторного признака на одну единицу при условии, что остальные факторы зафиксированы на среднем уровне и не меняются.

Пример: b₁ и b₂ - абсолютные показатели силы связи; нельзя сравнивать между собой, т.к. они измерены в разных единицах.

b₁ = ((r_yx1 – r_yx2 * r_x1x2) / (1 – r²_x1x2)) * δ_y/δ_x1; b₂ = ((r_yx2 – r_yx1 * r_x1x2) / (1 – r²_x1x2)) * δ_y/δ_x2

Относительные - показывают, на сколько % в среднем меняется результативный признак при изменении факторного признака на 1% при условии, что остальные факторы зафиксированы на среднем уровне и не меняются.

1. Стандартизованные коэффициенты регрессии (ß-коэффициенты).

ß_i = b_i * δ_xi / δ_y

Показывают, на сколько сигм (δ) изменится в среднем результат, если соответствующий фактор х_i изменится на 1 сигму (δ) при неизменном среднем уровне других факторов.

Преимущество стандартизованных коэфф. над коэфф. чистой регрессии: Т.к. все переменные – центрированы и нормированы, то стандартизованные коэфф. ß_i сравнимы между собой. Сравнивая их, можно ранжировать факторы по силе их воздействия на результат.

2. Частные коэффициенты эластичности

Э = b_i * x_{i ср} / y_ср

Показывают, на сколько % в среднем меняется результативный признак при изменении рассматриваемого факторного признака на 1 % при условии, что остальные факторы зафиксированы на среднем уровне и не меняются.

!!! Параметры b_i в степенной модели являются частными коэффициентами эластичности.

По значениям коэфф. Э. м. сравнивать факторы, ранжировать их.

Связь 1. и 2.: Э = b_i * δ_xi : ν_x/ δ_y : ν_y = ß_i * ν_y / ν_xi

!!! М.б. ситуация, когда эти две ранжировки факторов не совпадают. Происходит тогда, когда коэфф. вариации при таком факторе значительно высок.

21. Множественный коэффициент корреляции и коэффициент детерминации

Теснота связи – характеризует, насколько фактор или факторы, включенные в уравнение регрессии, объясняют изменение результата. Насколько близко фактические значения показателя расположены к линии регрессии. Чем ближе, тем теснее.

Коэффициент множественной детерминации R² - обобщенный показатель оценки построенного уровня регрессии; показывает долю вариации (дисперсии) результативного признака, объясняемую регрессией, в общей вариации результата.

R² = SS_R / SS_T = 1 - SS_E / SS_T.

Вывод: на R² % вариация признака зависит от включенного в модель фактора (- ов), остальные (1 - R²)% - зависит от прочих неучтенных факторов.

R² = [0; 1]. 0 – связи нет, 1 – связь функциональная.

1. (у_к – у_ср) – общее отклонение за счет всех факторов;

2. (у_к –у_{к с крыш}) – ошибка (остаток); отклонение за счет прочих неучтенных факторов;

3. (у_{к с крыш} – у_ср) – отклонение за счет учтенных факторов.

Если рассмотреть множество точек, то:

Σ(у – у_ср)² = Σ(у – у_{с крыш})² + Σ(у_{с крыш} – у_ср)²

SS_T = SS_R + SS_E

1. (у – у_ср) ² = SS_T - общая сумма квадратов отклонений;

2. (у – у_{с крыш}) ² = SS_R - факторная сумма квадратов отклонений;

3. (у_{с крыш} – у_ср) ² = SS_E - остаточная сумма квадратов отклонений.

Если разделить SS на n (количество единиц совокупности), то:

δ_T² = δ_R² + δ_E²

Коэфф. (индекс) множественной корреляции

Корень из R² = R = корень из (SS_R / SS_T)= корень из (1 - SS_E / SS_T);

R = [0; 1] – чем ближе к 1, тем теснее связь (а в парной = [-1; 1]).

Свойства R:

- R - стандартизованный коэффициент регрессии;

- если связи между х и у нет, то R = 0; НО если R = 0, то нет только линейной связи;

- R_ху = R_ух.

Шкала значения коэфф. корреляции:

1. До 0,3 связь слабая 2. 0,3-0,5 связь умеренная

3. 0,5-0,7 связь заметная 4. 0,7-0,9 связь высокая

5. 0,9-1,0 связь весьма высокая, близкая к функциональной.

Скорректированный (нормированный) коэфф. детерминации R²_скорр :

По R² можно сравнивать модели, НО необходимо пересчитать его на число степеней свободы, т.к. модели м. иметь разный набор факторов и разные числовые наблюдения.

R²_скорр = 1 – (SS_E : (n-m-1) / SS_T : (n-1)) = 1 – (1- R²) * ((n-1) / (n-m-1))

R²_скорр всегда больше, чем R²_факт.

22. Показатели частной корреляции

Коэфф. (индекс) множественной корреляции

Корень из R² = R = корень из (SS_R / SS_T)= корень из (1 - SS_E / SS_T);

R = [0; 1] – чем ближе к 1, тем теснее связь (а в парной = [-1; 1]).

Свойства R:

- R - стандартизованный коэффициент регрессии;

- если связи между х и у нет, то R = 0; НО если R = 0, то нет только линейной связи;

- R_ху = R_ух.

Шкала значения коэфф. корреляции:

1. До 0,3 связь слабая 2. 0,3-0,5 связь умеренная

3. 0,5-0,7 связь заметная 4. 0,7-0,9 связь высокая

5. 0,9-1,0 связь весьма высокая, близкая к функциональной.

Скорректированный (нормированный) коэфф. детерминации R²_скорр :

По R² можно сравнивать модели, НО необходимо пересчитать его на число степеней свободы, т.к. модели м. иметь разный набор факторов и разные числовые наблюдения.

R²_скорр = 1 – (SS_E : (n-m-1) / SS_T : (n-1)) = 1 – (1- R²) * ((n-1) / (n-m-1))

R²_скорр всегда больше, чем R²_факт.

Показатели частной корреляции основаны на соотношении сокращения остаточной вариации за счет дополнительно включенного в модель фактора к остаточной вариации до включения в модель соответствующего фактора.

Частные коэфф. корреляции (рекуррентные формулы - выражающие каждый член последовательности через предыдущих членов):

r_yx2.x1 = корень из ((SS_{E yx1} – SS_{E yx1x2}) / SS_{E yx1}) = к. из ((1 – SS_{E yx1x2}) / SS_{E yx1}), х₂ зафиксирован;

r_yx1.x2 = корень из ((SS_{E yx2} – SS_{E yx1x2}) / SS_{E yx2}) = к. из ((1 – SS_{E yx1x2}) / SS_{E yx2}), х₁ зафиксирован.

!!! Матрица частных коэфф. корреляции м.б. использована для отбора факторов в модель.

23. Оценка значимости уравнения множественной регрессии и его параметров

Значение коэфф. детерминации R² может отражать истинную зависимость, а может – стечение обстоятельств, т.к. при построении уравнения используются выборочные данные. Поэтому необходимо определить, насколько выборочные показатели (оценки) достоверны, значимы. Для этого используют вероятностные оценки стат. гипотез.

Статистическая гипотеза (Н) - предположение о свойстве генеральной совокупности, которое можно проверить, опираясь на данные выборки.

Этапы проверки статистических гипотез:

1. формулируется задача исследования в виде стат. гипотезы;

2. выбирается статистическая характеристика гипотезы;

3. выдвигаются испытуемая и альтернативная Н₀ и Н₁;

4. определяется ОДЗ, критическая область и критическое значение статистического критерия;

5. вычисляется фактическое значение статистического критерия;

6. испытуемая Н₁ проверяется на основе сравнения значений фактического и критического критерия, и в зависимости от результатов проверки Н₁ либо отклоняется, либо принимается.

Критическая область – область, попадание значения статистического критерия в которую приводит к отклонению Н₀ . Вероятность попадания значения критерия в эту область равна уровню значимости (1 минус доверительная вероятность).

ОДЗ - область, попадание значения статистического критерия в которую приводит к принятию Н₀.

I. Статистическая оценка достоверности регрессионной модели:

А. 1. выдвигается H₀: r² в генеральной совокупности = 0;

2. выдвигается H₁: r² в генеральной совокупности не = 0;

3. определяется ОДЗ или уровень значимости;

4. рассчитывается критерий Фишера F (n – число единиц совокупности, m – число факторов):

F = MS_R / MS_E = (Σ(y _{с крыш} – y_ср)² / m) / (Σ(y– y _{с крыш})² / (n-m-1))

F = R²/(1-R²) * (n-m-1)/m = R²/ (1-R²) * (n-2);

5. определяется табличное значение критерия Фишера F_табл;

6. фактическое значение сравнивается с табличным.

а. Если F>Fтабл., то гипотеза о случайной природе оцениваемых характеристик отклоняется и признается статистическая значимость и надежность.

б. Если F<Fтабл., то гипотеза о случ… не отклоняется и признается статистическая незначимость, ненадежность уравнения регрессии.

Вывод: с вероятностью α м. утверждать, что коэфф. детерминации R² в генеральной совокупности не значим; модель недостоверна.

Число степеней свободы (df) - число свободно варьируемых переменных.

df_T = df_R + df_E; n-1 = m + (n – m – 1).

При расчете фактической суммы квадратных отклонений ((у – у_{с крыш}) ² = SS_R) используются теоретические значения результативного признака (у_{с крыш}), определенного по линии регрессии (у_{с крыш} = a + bx). Т.к. объясненная (факторная) сумма квадратов зависит только от n констант, то данная модель имеет n степеней свободы.

Если разделить сумму квадратов на число степеней свободы, можно получить дисперсии на 1-у степень свободы (MS):

MS_R = SS_R/df_R = Σ(y _{с крыш} – y_ср)² / m

MS_Е = SS_Е/df_Е = Σ(y– y _{с крыш})² / (n-m-1)

Все показатели м. оформить в виде таблицы дисперсионного анализа ANOVA.

Источник вариации:	df	SS	MS	F
- регрессия	m	SSR	MSR	F
- остаток	n-m-1	SSE	MSE	–
- итого	n-1	SST	–	–

df – кол-во степеней свободы; MS = SS/df – дисперсия на 1 степень свободы; SS - сумма квадратов отклонений (общ., факт., остат.); F = MS_R/MS_E – критерий Фишера.

Б. Есть частные F-критерии, с помощью которых м. оценить дополнительное включение фактора в модель. Необходимость такой оценки связана с тем, что не каждый фактор в модели существенно увеличивает фактическую вариацию – поэтому нужно ли включать этот фактор в модель?

Важно, что из-за различной связи между факторов, значимость одного и того же доп. фактора различна в зависимости от порядка его включения в модель.

Частные F-критерии строятся на сравнении прироста факторов на 1 степень свободы за счет доп. включения в модель фактора к остаточной вариации до модели.

F_x1 = ((R²_yx1x2 – r²_yx2) / (1-R² _yx1x2)) * (n-m-1) = 0,96

F_x2 = ((R²_yx1x2 – r²_yx1) / (1-R² _yx1x2)) * (n-m-1) = 1,9

F_табл = 10.

Вывод: С вероятностью α м. утверждать, что включение фактора х₁ после х₂ не целесообразно, и включение х₂ после х₁ нецелесообразно – нельзя построить двухфакторную модель.

Все показатели м. оформить в виде частной таблицы дисперсионного анализа ANOVA.

Источник вариации:	df	SS	MS	F
- регрессия	2	SSR	MSR	F
- в т.ч. с ф. х2	1	SSRх2	MSRх2	F х2
- регрессия, обусл. вкл. в модель ф. x1 после x2	1	SSRх1	MSRх1	F х1
- остаток	3	SSE	MSE	–
- итого	5	–	–	–

df – кол-во степеней свободы; MS = SS/df – дисперсия на 1 степень свободы; SS_x2 = SS_T * r_2yx2 - сумма квадратов отклонений (общ., факт., остат.); F = MS_R/MS_E – критерий Фишера. F = t².