§ 7. Понятие линейного пространства

(продолжение)

3. Понятие линейной зависимости и независимости. Базис

Напомним, что если – некоторое множество, элементы которого можно складывать и умножать на числа, то выражение (где , , , , , , , – числа) называют линейной комбинацией элементов , , , с коэффициентами , , , . Если и является линейной комбинацией элементов , , , , т.е.

,

то говорят, что линейно выражается через элементы , , , .

Пусть – линейное пространство над ℝ(ℂ), , , , .

ОПРЕДЕЛЕНИЕ. Говорят, что векторы , , , линейно зависимы, если существуют числа , , , , не все равные нулю и такие, что линейная комбинация равна нулевому элементу линейного пространства .

Если же равенство возможно только при условии , то векторы , , , называют линейно независимыми.

Справедливо следующее утверждение.

ЛЕММА 4. Векторы , , , линейно зависимы тогда и только тогда, когда хотя бы один из них линейно выражается через оставшиеся.

ДОКАЗАТЕЛЬСТВО

1) Необходимость.

Пусть векторы , , , – линейно зависимы. Тогда по определению существуют числа , , , , не все равные нулю и такие, что

.

Пусть, например, . Тогда

,

.

2) Достаточность.

Пусть один из векторов , , , линейно выражается через оставшиеся. Например, пусть

.

.

Следовательно, векторы , , , – линейно зависимы.

Замечание. Часто в качестве определения линейно зависимых векторов берут формулировку леммы 4.

ПРИМЕРЫ.

1) Рассмотрим матрицы

, , , , .

Матрицы , , , , – линейно зависимы, матрицы , , , – линейно независимы.

2) Многочлены , , , – линейно зависимы, так как является линейной комбинацией , , .

Многочлены , , , – линейно независимы.

3) Пусть , , . Выясним, является ли эта система векторов пространства ℝ линейно зависимой. Пусть .

Тогда имеем:

.

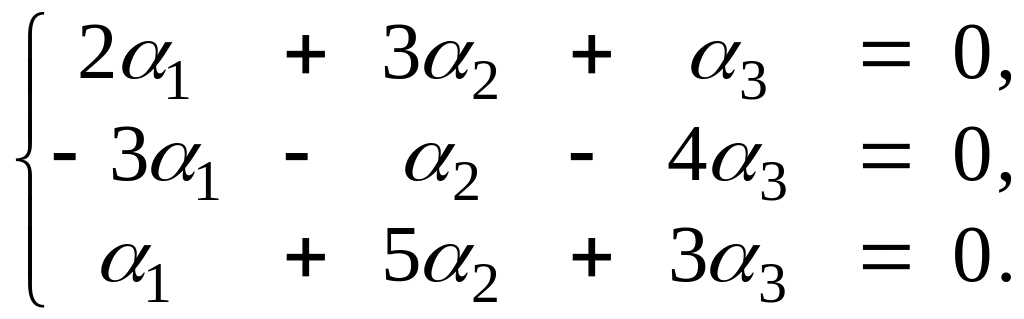
Таким образом, векторы , , будут линейно независимыми, если – единственное решение системы. Согласно критерию единственности решения системы (см. §4) это будет иметь место, если , где – матрица системы, – число неизвестных.

В нашем случае имеем: ,

.

Следовательно, система имеет только тривиальное решение , и, значит, векторы , , – линейно независимые.

Теперь рассмотрим произвольных векторов из ℝ :

, , , .

Эти векторы всегда будут линейно зависимы. Действительно, рассмотрение линейной комбинации приведет нас к системе уравнений

Так как – матрица размера и , то ее ранг . Следовательно, система будет иметь нетривиальные решения, и, значит равенство возможно не только при нулевых коэффициентах.

Таким образом, мы можем утверждать, что в пространстве ℝ линейно независимых векторов может быть не более трех.

ОПРЕДЕЛЕНИЕ. Максимальная линейно независимая система векторов линейного пространства называется базисом этого линейного пространства.

Иначе говоря, векторы , , , образуют базис в линейном пространстве если выполняются два условия:

1. , , , – линейно независимы;

2. , , , , – линейно зависимы для любого вектора из .

Очевидно, что в линейном пространстве существует не единственный базис (например, легко доказать, что если , , , образуют базис в линейном пространстве и , , , – отличные от нуля действительные числа, то векторы , , , тоже будут базисом). Но справедлива следующая теорема.

ТЕОРЕМА 5. Любые два базиса линейного пространства состоят из одного и того же числа векторов.

Если в линейном пространстве существует базис из векторов, то пространство называют конечномерным, а называют размерностью линейного пространства (пишут: ).

Если в линейном пространстве для любого натурального можно найти линейно независимую систему векторов, то пространство называют бесконечномерным (пишут: ).

ПРИМЕРЫ.

1) Линейное пространство ℝ матриц второго порядка с элементами из ℝ имеет размерность ℝ . Его базисом будут, например, матрицы

, , , .

Базис , , , в дальнейшем будем называть стандартным базисом пространства ℝ .

2) Множество свободных векторов плоскости является конечномерным линейным пространством. Его размерность . Базисом будут являться любые два неколлинеарных вектора.

Действительно, пусть , – неколлинеарные векторы на плоскости. Покажем, что они линейно независимы. Пусть

.

Предположим, что хотя бы один из коэффициентов этой линейной комбинации отличен от нуля. Например, . Тогда

,

и, значит, векторы и – коллинеарные. Следовательно, предположение неверно и линейная комбинация векторов , равна нулевому вектору только при , что и означает линейную независимость векторов , .

Т еперь покажем, что любой вектор можно представить в виде линейной комбинации векторов и . Для этого построим векторы , и . Через точку проведем прямые параллельные векторам и . Точки пересечения этих прямых и прямых, на которых лежат векторы и , обозначим соответственно и . По правилу параллелограмма имеем:

.

Но векторы и коллинеарны, и, следовательно,

для некоторого ℝ. Аналогично

.

Таким образом, получили

.

3) Линейное пространство свободных векторов пространства имеет размерность . Легко доказать, что базисом в пространстве являются любые три некомпланарных вектора.

Замечание. Хотя в качестве базиса на плоскости (в пространстве) можно взять любые два неколлинеарных (любые три некомпланарных) вектора, на практике предпочитают работать с декартовым прямоугольным базисом , ( , , ). Это единичные векторы, которые сонаправлены координатным осям и соответственно (сонаправлены координатным осям , и соответственно).

4) Арифметическое линейное пространство ℝ тоже является конечномерным. Его размерность ℝ . Базисом будут являться, например, векторы

, , ,

(будем называть его стандартным базисом пространства ℝ ).

5) Пусть задана некоторая система линейных однородных уравнений , имеющая нетривиальные решения. Множество ℋ ее решений является конечномерным линейным пространством. Его базисом будет фундаментальная система решений, и, следовательно, ℋ , где – число неизвестных, – ранг матрицы

6) Линейное пространство ℝ многочленов с коэффициентами из ℝ является бесконечномерным. Легко проверить, что для любого натурального многочлены

, , , ,

будут линейно независимы.

Роль базиса в линейном пространстве характеризует следующая теорема.

ТЕОРЕМА 6 (о базисе). Каждый вектор линейного пространства линейно выражается через любой его базис, причем единственным образом.

ДОКАЗАТЕЛЬСТВО

Пусть , , , – базис линейного пространства и – произвольный вектор из . Тогда, по определению, , , , – линейно независимы, а , , , , – линейно зависимы. Следовательно, существуют числа , , , , не все равные нулю и такие, что линейная комбинация

.

Причем, коэффициент не может быть равен нулю.

Действительно, если , то , где коэффициенты , , , не все равны нулю. Так как существует нулевая линейная комбинация элементов , , , с коэффициентами, среди которых есть ненулевые, то , , , – линейно зависимые. Но они по условию образуют базис, и, следовательно, линейно независимы.

Так как , то линейно выражается через , , , :

,

.

Теперь докажем, что линейно выражается через базис единственным образом. Предположим противное. Пусть

и ,

причем хотя бы для одного . Пусть для определенности . Тогда

,

.

Так как , то . Таким образом, получили, что существует нулевая линейная комбинация векторов , , , , среди коэффициентов которой есть ненулевые. Значит , , , – линейно зависимые. Но они по условию линейно независимы, так как образуют базис.

Следовательно, предположение неверное и вектор разлагается по базису , , , единственным образом.