
3.4 Швидке перетворення Фур’є
Перетворення Фур’є широко використовується в інженерній практиці для аналізу як періодичних, так і неперіодичних сигналів.
Перетворення Фур’є дійсної
функції
![]() ,
яка визначена на нескінченому інтервалі,
обчислюється за формулою
,
яка визначена на нескінченому інтервалі,
обчислюється за формулою
![]() ,
,
де
![]() - частота;
- частота;
- уявна одиниця.
Якщо область інтегрування
не обмежена, то у загальному випадку
перетворення Фур’є не існує. Для
кінцевого інтервалу часу
![]() можна отримати фінітне перетворення
Фур’є
можна отримати фінітне перетворення
Фур’є
![]() .
.
Допустимо, що величина
спостерігається у дискретні моменти
часу
![]() ,
де
,
де
![]() ,
,
![]() ;
;
![]() - крок дискретності. Тоді інтеграл в
останньому співвідношенні можна замінити
сумою
- крок дискретності. Тоді інтеграл в
останньому співвідношенні можна замінити
сумою
![]() .
.
Для обчислення
![]() вибирають , як правило, дискретні значення
частот
вибирають , як правило, дискретні значення
частот
![]() ,
,
![]() .
.
Тоді
![]() .
.
Підставляючи в останню формулу
замість
![]() його значення, отримуємо
його значення, отримуємо
![]() .
.
Якщо ввести позначення
![]() ,
то
,
то
![]() ,
(3.6)
,
(3.6)
Величина
![]() носить назву множника
повороту.
носить назву множника
повороту.
Вектор
![]() називається дискретним
перетворенням Фур’є
(Discrete Fourier Transform, DFT) вектора
називається дискретним
перетворенням Фур’є
(Discrete Fourier Transform, DFT) вектора
![]() і позначається таким чином:
і позначається таким чином:
![]() .
.
В алгоритмі дискретного перетворення Фур’є використовуються властивості комплексних коренів із одиниці.
Комплексним коренем степені
із одиниці називають
таке комплексне число
![]() ,
що
,
що
![]() .
(3.7)
.
(3.7)
Рівняння (3.7) має рівно комплексних коренів
![]() ,
(3.8)
,
(3.8)
де
;
![]() - уявна одиниця.
- уявна одиниця.
Комплексні корені із одиниці рівномірно розподілені на колі одиничного радіуса з центром у нулі (рис. 3.5). Значення
![]() (3.9)
(3.9)
називається головним
значенням кореня степені
![]() із одиниці. Інші корені
із одиниці є його степенями.
із одиниці. Інші корені
із одиниці є його степенями.
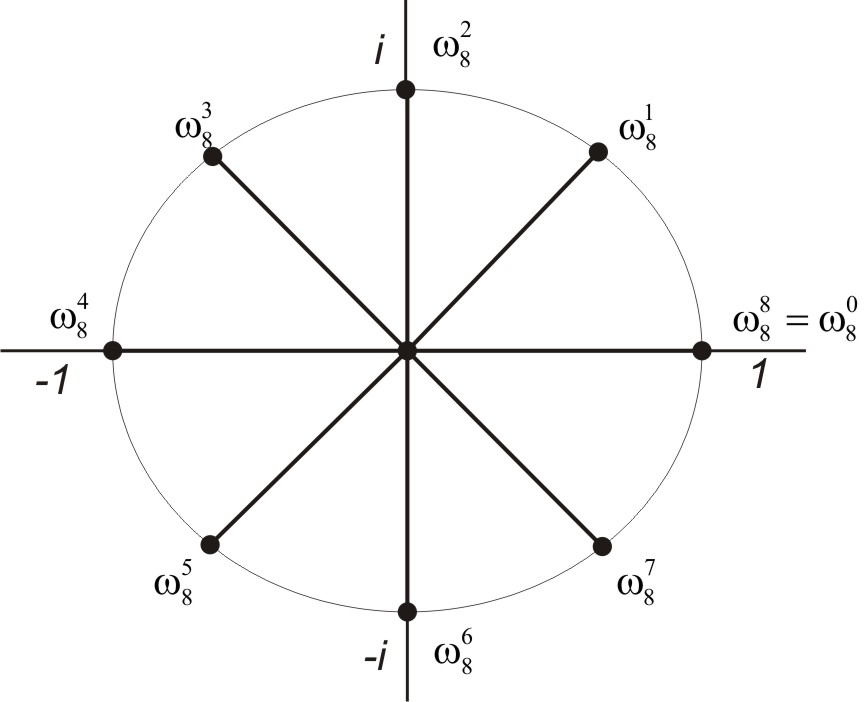
Рисунок 3.5 – Значення
![]() на комплексній площині (
на комплексній площині (![]() )
)
Наведемо основні властивості коренів із одиниці.
Властивість 1.
для будь-яких цілих
![]() ,
,
![]() і
і
![]()
![]() .
(3.10)
.
(3.10)
У відповідності з (3.8)
![]() .
(3.11)
.
(3.11)
Властивість 2.
Для будь-якого парного
![]()
![]() .
(3.12)
.
(3.12)
Використовуючи співвідношення
(3.8), можемо записати
![]() .
Згідно формули Ейлера
.
Згідно формули Ейлера
![]() .
Із рівності (3.9) випливає, що
.
Із рівності (3.9) випливає, що
![]() ,
тобто має місце формула (3.11).
,
тобто має місце формула (3.11).
Властивість 3 (ділення
наполовину). Якщо
парне, то, піднісши до квадрату всі
комплексних коренів степені
із одиниці, отримаємо всі
![]() комплексні корені степені
із одиниці.
комплексні корені степені
із одиниці.
Оскільки
![]() ,
то з врахуванням (3.12), маємо
,
то з врахуванням (3.12), маємо
![]() .
Із останньої рівності випливає, що
.
Із останньої рівності випливає, що
![]() .
Розглянемо величину
.
Розглянемо величину
![]() .
Із властивості 1, коли
.
Із властивості 1, коли
![]() випливає, що
випливає, що
![]() .
Так як
.
Так як
![]() ,
то
,
то
![]() .
.
Властивість 4
(додавання). Для будь-якого
![]() і невід’ємного числа
,
яке не є кратним до
,
має місце рівність
і невід’ємного числа
,
яке не є кратним до
,
має місце рівність
![]() .
(3.13)
.
(3.13)
Ряд
![]() представляє собою геометричну прогресію,
у якої перший член -
,
знаменник -
представляє собою геометричну прогресію,
у якої перший член -
,
знаменник -
![]() і останній член прогресії
і останній член прогресії
![]() .
Тому
.
Тому
![]() .
Оскільки
.
Оскільки
![]() .
Оскільки
.
Оскільки
![]() ,
то
,
то
![]() .
Отже, маємо
.
Отже, маємо
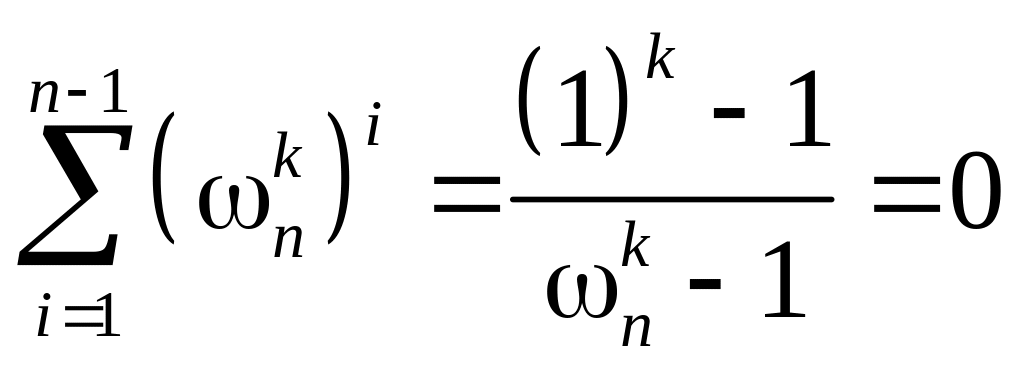 .
.
Знаменник не перетворюється у нуль, так як не кратне .
У формулі (3.6) введемо позначення:
![]() .
Тоді формула (3.6) набуде такого вигляду:
.
Тоді формула (3.6) набуде такого вигляду:
![]() .
(3.14)
.
(3.14)
Таким чином, FFT-задача
трансформувалась у задачу обчислення
значень многочлена (3.14) степені
у коренях степені
із одиниці, тобто у точках
![]() ,
,
![]() ,
,
![]() ,
…,
,
…,
![]() .
.
Для розв’язку FFT-задачі
використаємо метод «розділяй і володарюй».
Допускаємо, що степінь полінома (3.14) є
степеню числа 2, тобто
![]() ,
де
,
де
![]() - ціле додатне число. Якщо це не так, то
поліном (3.14) доповнюється до полінома
степені
- ціле додатне число. Якщо це не так, то
поліном (3.14) доповнюється до полінома
степені
![]() ,
з нульовими коефіцієнтами при відповідних
степенях. Утворимо два поліноми
,
з нульовими коефіцієнтами при відповідних
степенях. Утворимо два поліноми
![]() і
і
![]()
![]() ,
,
![]() ,
,
кожний із яких є поліномом
степені
![]() .
Дальше ділимо
.
Дальше ділимо
![]() на поліноми
на поліноми
![]() і
і
![]() .
У результаті отримаємо два поліноми
.
У результаті отримаємо два поліноми
![]() і
і
![]() та
відповідні залишки
та
відповідні залишки
![]() і
і
![]() мають степінь не більшу ніж
мають степінь не більшу ніж
![]() кожний, тобто
кожний, тобто
![]() або
або
![]() .
Обчислення
у точці
.
Обчислення
у точці
![]() рівносильне знаходженню залишку від
ділення на
рівносильне знаходженню залишку від
ділення на
![]() (це випливає з того, що у такому випадку
можна записати у такому вигляді:
(це випливає з того, що у такому випадку
можна записати у такому вигляді:
![]() ,
де
,
де
![]() - постійна величин. Тоді
- постійна величин. Тоді
![]() ).
).
Оскільки при
,
де
![]() ,
,
![]()
![]() ;
у тому випадку, коли
;
у тому випадку, коли
![]()
![]() і
і
![]() .
Таким чином, знаходження
.
Таким чином, знаходження
![]() при
рівноцінно знаходження залишку від
ділення
на
.
Аналогічно для знаходження
при
необхідно поліном
поділити на
і знайти залишок від такого ділення.
Рекурсивне застосування тактики
«розділюй і володарюй» є значно
ефективнішим прямолінійного ділення
на кожний дільник
.
при
рівноцінно знаходження залишку від
ділення
на
.
Аналогічно для знаходження
при
необхідно поліном
поділити на
і знайти залишок від такого ділення.
Рекурсивне застосування тактики
«розділюй і володарюй» є значно
ефективнішим прямолінійного ділення
на кожний дільник
.
У тому випадку, коли
степінь числа 2, то швидке перетворення
Фур’є має степінь складності
![]() .
.
