3.3 Множення матриць

Матриця - математичний об’єкт, який задається таблицею чисел , , . Числа і визначають розмір матриці , тобто матриця має рядків і стовпців; на перетині -го рядка та -го стовпця знаходиться елемент матриці . Отже, матриця розміром задається таблицею чисел

.

Дві матриці і однакового розміру можна додавати чи віднімати у результаті отримаємо матрицю чи , у якій або , , .

Якщо число стовпців матриці співпадає з числом рядків матриці , то такі матриці можна перемножувати, тобто . У тому випадку коли матриці і мають розміри і відповідно, то елементи матриці обчислюються за такою формулою:

, , . (3.2)

У результаті виконання операції (3.2) отримаємо матрицю розміром .

У загальному випадку , тобто операція множення матриць не комутативна.

Стандартний алгоритм множення двох матриць і розмірами і має наступний вигляд:

MatrixMultiply

1 Визначити розміри матриць А і В – m,r,n

2 for i=1 to m

3 for j=1 to n

4 C(i,j)=0

5 for k=1 to r

6 C(i,j)=C(i,j)+A(i,k)*B(k,j)

7 end for

8 end for

9 end for

Алгоритм MatrixMultiply множення матриць і розмірами і виконує операцій множення і операцій додавання. Загальна кількість операцій, що виконує алгоритм MatrixMultiply при перемноженні двох матриць, дорівнюватиме .

Крім стандартного алгоритму множення матриць відомі ще такі алгоритми як Винограда та Штрассена, які є ефективнішими за стандартний алгоритм. Якщо, наприклад, перемножуються дві квадратні матриці розмірами , то наочне уявлення про ефективність кожного із трьох алгоритмів дає табл. 3.1

Таблиця 3.1 – Порівняння ефективності трьох

алгоритмів

Алгоритм	Операції
	множення	додавання
Стандартний
Винограда
Штрассена

Економія обчислювальних ресурсів при використанні алгоритмів Винограда чи Штрассена проявляється при множенні матриць великої розмірності, що досягається шляхом ускладнення відповідних алгоритмів. Алгоритм Штрассена на практиці застосовується рідко. Застосування його виправдано для щільних матриць (таких, що вміщують мало нулів) і, розмір яких досить великий (приблизно ). Матриці невеликого розміру рекомендується перемножувати за допомогою стандартного алгоритму.

Ми розглянули алгоритм перемноження двох матриць і . На практиці зустрічаються задачі, коли необхідно знайти добуток ланцюжка матриць

, (3.3)

де матриця має розмір , .

Ланцюжок матриць (3.3) можна перемножувати природнім способом – зліва направо. При множенні матриці на розмірами і отримаємо матрицю розміром . Потім до матриць та застосовуємо операцію множення, що дає змогу отримати матрицю розміром і т. д.

Виявляється, що кількість операцій, які необхідно затратити для пошуку добутку ланцюжка матриць (3.3) можна значно скоротити, якщо порядок множення матриць визначити певною розстановкою дужок. Нагадаємо, що операція множення матриць володіє властивістю асоціативності, тому результат не залежить від способу розстановки дужок. Наприклад, якщо задана послідовність матриць , то спосіб їх обчислення повністю визначається за допомогою розстановки дужок п’ятьма різними варіантами

,

,

,

,

.

Час обчислення добутку матриць визначається кількістю скалярних добутків, які обчислюються у рядку 6 процедури MatrixMultiply. Ця кількість дорівнює . Якщо -ту лінійку матриці та -тий стовпець матриці розглядати як вектори з компонентами і , то під скалярним добутком будемо розуміти операцію знаходження елемента матриці як скалярний добуток двох векторів .

Щоб проілюструвати як спосіб розстановки дужок при перемноженні декількох матриць впливає на кількість операцій, що виконуються, розглянемо приклад, у якому перемножуються три матриці . Допустимо, що розміри цих матриць – , та . Перемножуючи ланцюжок матриць у природному порядку – зліва направо; спочатку отримаємо матрицю , а потім матрицю . Розміри матриць і відповідно дорівнюють і відповідно, де , і . Матриця буде мати розмір . Для обчислення всіх елементів матриці необхідно обчислити скалярних добутків. Знаходження елементів матриці , яка матиме розмір , потребує . Разом будемо мати 5000+2500=7500 скалярних множень. Якщо обчислити результат, який задається виразом , то неважко підрахувати, що отримаємо 75000 скалярних множень. Таким чином, для обчислення першим способом добутку ланцюжка матриць затрати часу будуть у 10 раз менші, ніж у другому випадку.

Задачу про перемноження послідовності матриць сформулюємо наступним чином: для заданої послідовності матриць , в якій матриця має розмір , за допомогою дужок повністю визначити порядок множення у матричному добутку , при якому кількість скалярних множень буде мінімальною.

Звернемо увагу на те, що операція перемноження матриць у задачу не входить. Мета розв’язку поставленої задачі – визначити оптимальний порядок перемноження матриць.

Сформульована задача, у принципі, може бути розв’язана шляхом перебору всіх можливих варіантів розстановки дужок у матричному добутку . Позначимо через кількість альтернативних способів розстановки дужок у послідовності, що складається із матриць. Якщо , то порядок розстановки дужок повністю визначений і - . При величину можна визначити із рекурентного співвідношення

(3.4)

Розв’язком рекурентної співвідношення (3.4) є так звана послідовність чисел Каталана, яка зростає як . Таким чином, кількість варіантів розстановки дужок має експоненціальне збільшення зі зростанням , і метод прямого перебору не є ефективним для визначення оптимальної стратегії розстановки дужок.

Для розв’язку поставленої задачі застосуємо алгоритмічну стратегію динамічного програмування.

Позначимо результат перемноження матриць через , де . Якщо задача нетривіальна, то будь-який спосіб розстановки дужок розбиває добуток між матрицями і , де - ціле число, що задовольняє умові . Таким чином, при деякому спочатку обчислюються матриці і , а потім вони перемножуються між собою і у результаті отримуємо добуток . Вартість, яка визначається вибраним способом розстановки дужок дорівнює сумі вартості обчислення матриці , вартості обчислення матриці та вартості обчислення добутку матриць і .

Нехай мінімальна кількість скалярних добутків необхідних для обчислення матриці . Тоді повна вартість мінімальної кількості скалярних добутків для обчислення буде - .

Оскільки початкову задачу ми розбили на дві підзадачі, то величина дорівнює сумі мінімальних вартостей обчислення часткових добутків і плюс вартість множення матриць і одну на одну. Якщо врахувати, що кожна матриця має розмір , то неважко зрозуміти, що для обчислення добутку матриць і знадобиться скалярних добутків, тобто

. (3.5)

У рекурсивному співвідношенні невідомою є величина . Для знаходження значення є можливостей, а саме - , тобто

(3.6)

В описаній нижче процедурі MatrixChainOrder допускається, що розміри матриці - , . Вхідні дані – це послідовність , розмір якої . у процедурі використовується допоміжна таблиця для зберігання вартостей . Таблиця використовується для побудови оптимального рішення. У ході виконання алгоритму таблиця заповнюється у порядку збільшення довжини послідовності матриць.

MatrixChainOrder

1 n=length(p)

2 for i=1 to n

3 m(i,i)=0

4 end for

5 for l=2 to n

6 for i=1 to n-l+1

7 j=i+l-1

8 m(i,j)=

9 for k=i to j-1

10 q=m(i,k)+m(k+1,j)+p_i-1p_kp_j

11 if q< m(i,j)

12 then m(i,j)=q

13 s(i,j)=k

14 end if

15 end for

16 end for

17 end for

Спочатку в процедурі MatrixChainOrder (рядки 2 – 4) величинам присвоюється нульове значення, що відповідає послідовності нульової довжини. У першій ітерації циклу (рядки 5 – 16) за допомогою рекурентного співвідношення (3.6) обчислюються величини при - мінімальні вартості для послідовностей довжини . При другому проході цього ж циклу обчислюються величини при - мінімальні вартості для послідовностей довжини . і т. д. На кожному етапі уже вичислені у рядках 9 – 17 величина залежать тільки від попередньо обчислених і занесених у таблицю значень і .

Оптимальне значення нескладно знайти за допомогою інформації, що зберігається у таблиці . Кожний елемент таблиці вміщує індекс , де при оптимальному розміщенні дужок у послідовності виконано розбиття. . Таким чином, нам відомо, що оптимальне обчислення добутку матриць виглядає наступним чином: . Ці часткові добутки матриць можна обчислити рекурсивно, оскільки елемент визначає матричне множення, що виконується останнім при обчисленні , а - останнє множення при обчисленні .

Приклад 3.3 Для матриць, розміри яких наведені у табл. 3.2 визначити оптимальну розстановку дужок з використанням процедури MatrixChainOrder.

Оскільки використовується тільки частина таблиці у якій елементи визначені тільки при , то використовується тільки та її частина, що розміщена над верхньою діагоналлю (рис. 3.4). На рис. 3.4 таблиця повернута таким чином, щоб її головна діагональ розмістилась горизонтально. Із даної таблиці легко знайти мінімальну вартість часткового добутку матриць .Вона знаходиться на пересіченні ліній, що йдуть від матриці вправо і вгору, і від матриці - вліво і вгору. У кожному горизонтальному рядку матриці знаходяться вартості перемноження часткових послідовностей, які складаються з однакової кількості матриць. У процедурі рядки обчислюються знизу вверх, а елементи у кожному рядку - зліва направо. із таблиці видно, що мінімальна вартість скалярних добутків, яка необхідна для перемноження шести матриць із табл. 3.2, дорівнює 15125. Таблиця дає змогу визначити порядок розстановки дужок у добутку матриць . У верхній клітинці таблиці знаходиться значення , яке розбиває добуток матриць на два співмножники і . Оскільки , то оптимальна розстановка дужок у добутку матриць буде такою: .

Таблиця 3.2 – Матриці та їх розміри

Матриця	Розмір

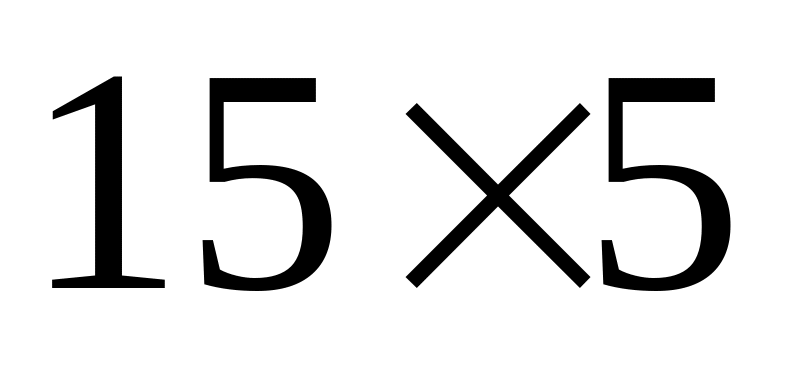
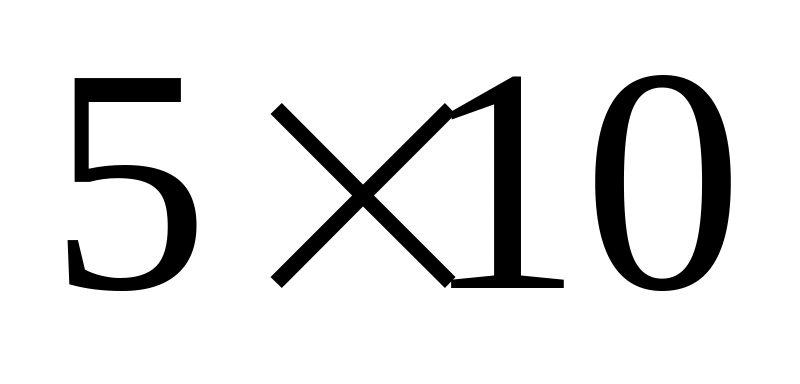
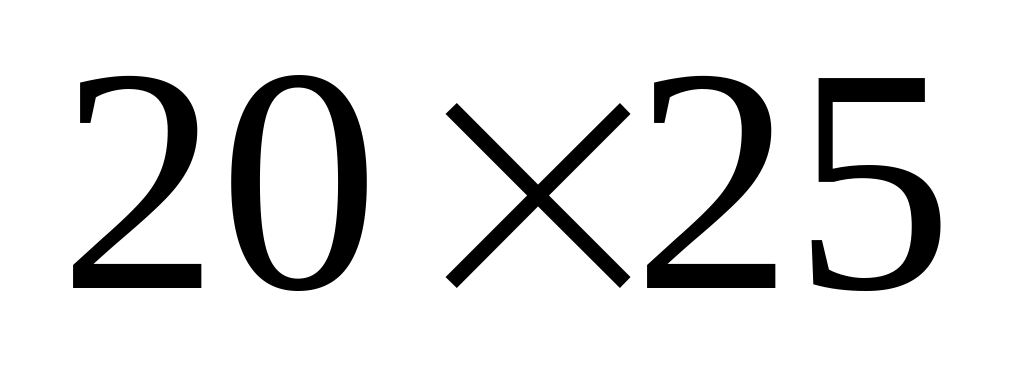
Для порівняння підрахуємо кількість скалярних добутків шести матриць, коли множення здійснюється зліва направо (природнім чином) (табл. 3.3).

Рисунок 3.4 – Таблиці та , що обчислюються процедурою MatrixChainOrder для

Порівняльний аналіз отриманих результатів показує, що при використанні процедури MatrixChainOrder кількість скалярних добутків при перемноженні шести матриць є значно меншою ніж при природному їх множенні.

Аналіз структури вкладених циклів у процедурі MatrixChainOrder показує, що час її роботи складає . Для збереження таблиць і необхідний обсяг пам’яті складає .

Таким чином, процедура MatrixChainOrder значно ефективніша, ніж метод перебору і повірки всіх можливих варіантів розстановки дужок, час роботи якого експоненціально залежить від кількості матриць, що перемножуються.

Таблиця 3.3 – Скалярні добутки матриць при природному їх

множенні

Часткові добутки матриць	Розмір матриці	Скалярні добутки
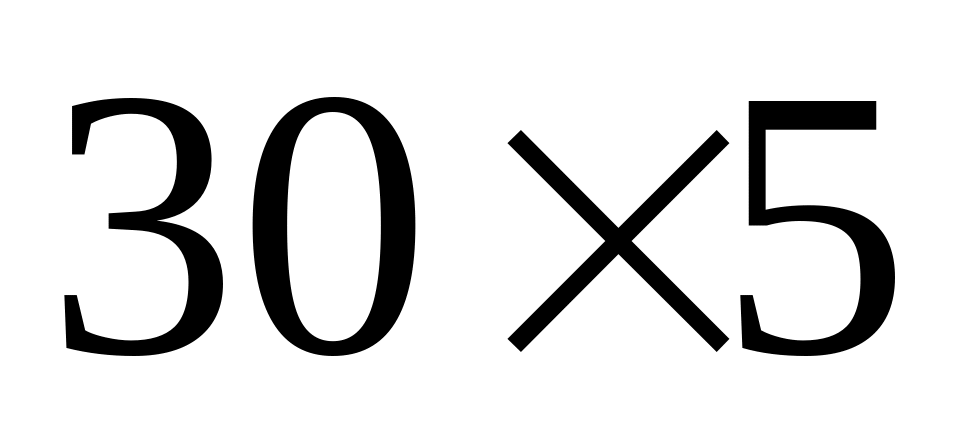
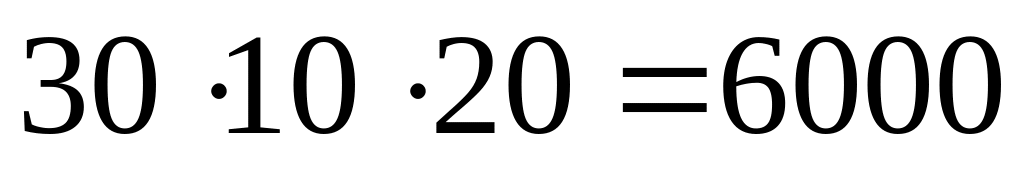
Загальна кількість скалярних добутків		40500