
- •Загальні рекомендації
- •. Огляд засобів розробки програм
- •1 Загальні поняття
- •2 Системи програмування
- •3 Технології програмування
- •3.1 Алгоритмічне (модульне) програмування
- •3.2 Структурне програмування
- •3.3 Подієво-орієнтоване програмування
- •3.4 Об'єктно-орієнтоване програмування
- •3.5 Візуальне програмування
- •Запитання для контролю та самоконтролю
- •. Основні поняття алгоритмізації
- •1. Поняття алгоритму. Властивості алгоритму
- •2. Способи подання (опису) алгоритму
- •3. Правила оформлення блок-схем алгоритмів
- •4. Базові алгоритмічні конструкції
- •Запитання для контролю та самоконтролю
- •. Етапи розв’язування прикладних задач
- •1. Постановка задачі
- •2. Побудова моделі
- •3. Розробка алгоритму
- •4. Вибір структур даних
- •5. Розробка програми
- •6. Тестування програми
- •7. Аналіз результатів роботи програми
- •8. Корисні технологічні правила програмування
- •Запитання для контролю та самоконтролю
- •V. Практикум з програмування. Turbo pascal
- •Робота з інтегрованим середовищем розробника
- •Запитання для контролю та самоконтролю
- •Тема №1 структура програми. Лінійна програма. Введення/виведення. Типи даних Теоретичні відомості
- •Var перелік імен змінних та їх типів;
- •Приклад
- •Варіанти завдань
- •Запитання для контролю та самоконтролю
- •Тема №2 програми розгалуженої структури Теоретичні відомості
- •Приклад
- •Варіанти завдань
- •Запитання для контролю та самоконтролю
- •Тема №3 цикли з параметром Теоретичні відомості
- •Приклад
- •Варіанти завдань
- •Запитання для контролю та самоконтролю
- •Тема №4 цикли з невідомим числом повторень Теоретичні відомості
- •Приклад
- •Варіанти завдань
- •Запитання для контролю та самоконтролю
- •Тема №5 використання масивів Теоретичні відомості
- •Var Ім'я : array[поч_індекс . . Кін_індекс] of Тип_даних;
- •Var Ім'я:array[поч_індекс1..Кін_індекс1,
- •Приклад
- •Варіанти завдань
- •Запитання для контролю та самоконтролю
- •Тема №6 символьний тип даних, рядки Теоретичні відомості
- •Приклад
- •Варіанти завдань
- •Запитання для контролю та самоконтролю
- •Тема № 7 використання допоміжних програм Теоретичні відомості
- •Приклад
- •Варіанти завдань
- •Запитання для контролю та самоконтролю
- •Тема № 8 використання множин Теоретичні відомості
- •Приклад
- •Варіанти завдань
- •Запитання для контролю та самоконтролю
- •Тема № 9 обробка записів Теоретичні відомості
- •Var Ім’я_запису : Ім’я_типу;
- •Приклад
- •Варіанти завдань
- •Запитання для контролю та самоконтролю
- •Тема № 10 організація обробки файлів Теоретичні відомості
- •Приклад
- •Варіанти завдань
- •Запитання для контролю та самоконтролю
- •Рекомендована література
Приклад
Скласти
таблицю значень функції ex
в інтервалі
![]() з кроком 1.
з кроком 1.
x - дійсне число, яке змінюється від -5 до 5 із кроком 1.
Для знаходження значень функції скористаємося стандартною (убудованою) функцією exp(x). Значення x обчислюємо за формулою: x=x+h, де h=1.
Число
повторень n
обчислюється за формулою:
![]() .
.
А
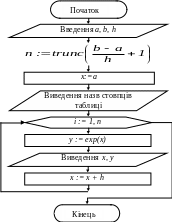 лгоритм:
лгоритм:

Вибираємо т
 ипи
даних: a,
b, h, x, y
- дійсний тип, i,
n
- цілий тип.
ипи
даних: a,
b, h, x, y
- дійсний тип, i,
n
- цілий тип.Текст програми:
program p3;
var a, b, h, x, y: real; i, n: integer;
begin
writeln('Введіть ліву границю, праву границю та крок');
readln(a,b,h);
n:=trunc((b-a)/h+1);
x:=a;
writeln(' Таблиця значень функції');
writeln('____________________________');
writeln('| x | y |');
for i:=1 to n do begin
y:=exp(x);
writeln('|',x:4:0,' |',y,' |');
x:=x+h;
end;
writeln('____________________________');
end.
Тестовий приклад: Для x=0 функція y=ex приймає значення 1.
Робочий розрахунок:
Введіть ліву границю, праву границю та крок
-5 5 1
Таблиця значень функції
____________________________
| x | y |
| -5 | 6.7379469991E-03 |
| -4 | 1.8315638889E-02 |
| -3 | 4.9787068368E-02 |
| -2 | 1.3533528324E-01 |
| -1 | 3.6787944117E-01 |
| 0 | 1.0000000000E+00 |
| 1 | 2.7182818285E+00 |
| 2 | 7.3890560989E+00 |
| 3 | 2.0085536923E+01 |
| 4 | 5.4598150033E+01 |
| 5 | 1.4841315910E+02 |
____________________________
Варіанти завдань
Скласти таблицю функції tg(x) на інтервалі (0°,45°) із кроком 5°.
Обчислити частоту використання цифри c у n-значному (n<9) цілому числі a.
Обчислити кількість цілих чисел на проміжку (A,B) які складаються з непарних цифр.
Для натурального числа n обчислити
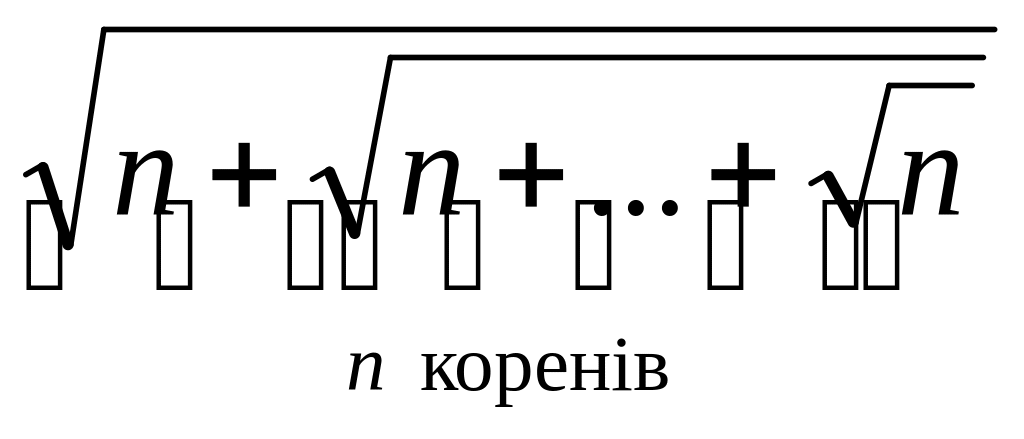 .
.Для натурального числа n обчислити значення виразу 1*2*3+2*3*4+…+n*(n+1)*(n+2).
Для натурального числа k обчислити значення k!! За формулою
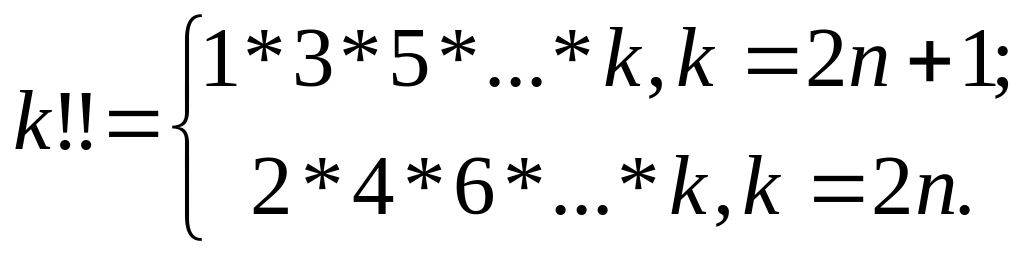
Для натурального числа m обчислити значення m2, користуючись наступною схемою: 12=1, 22=1+3, 32=1+3+5, . . .
Для натурального числа n<10 обчислити y=1!+2!+3!+…+n!.
У кінцевій послідовності, що складається з К невід’ємних цілих чисел, знайти максимальний елемент, що ділиться на 3 без залишку.
Для натурального числа n обчислити
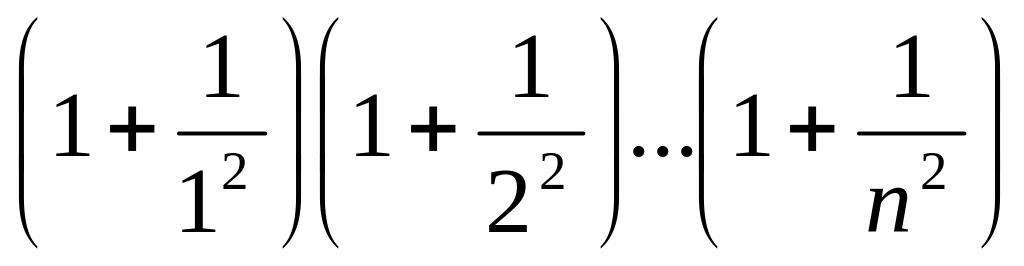 .
.Вивести на екран усі прості числа, що належать діапазону [2,n].
Обчислити суму m останніх цифр цілого числа с.
Визначити, чи є натуральне число n досконалим, тобто дорівнює сумі всіх своїх додатних дільників, крім самого цього числа. Наприклад, число 6 є досконалим: 6=1+2+3.
Для натурального числа n обчислити
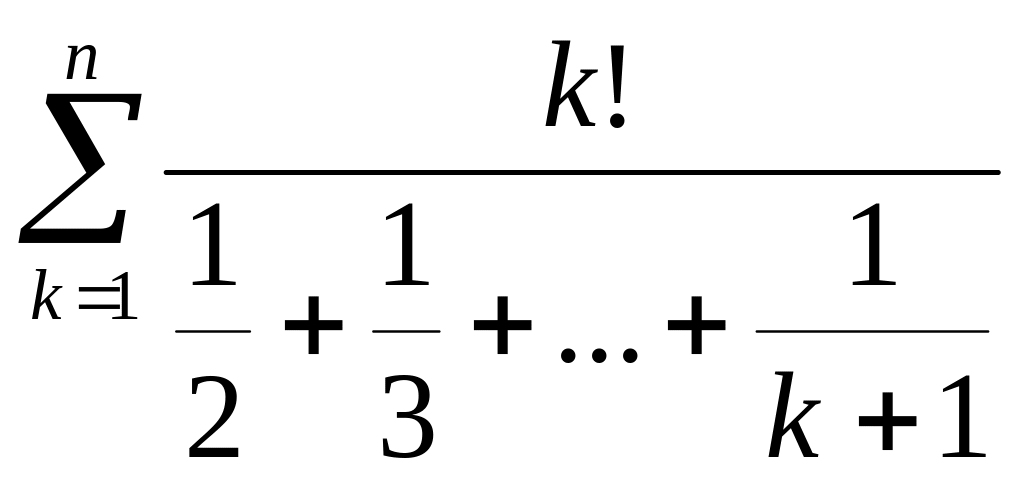 .
.Знайти всі додатні прості дроби, знаменник яких менший за а.
Вивести на екран у зростаючому порядку всі трьохзначні числа, що не мають у десятковому записі цифр, які повторюються.
Три натуральних числа k, l, m визначають піфагорову трійку, якщо k2+l2=m2. Для натурального числа n знайти всі піфагорові трійки чисел, менших за n.
Вивести на екран таблицю відповідності між вагою у фунтах та вагою у кілограмах для значень 10, 20, ... , 250 фунтів, врахувавши, що 1 фунт = 453 грам.
У послідовності чисел визначити кількість змін знаку.
У послідовності чисел відібрати всі додатні цілі числа та визначити їх середнє геометричне.
Визначити, чи є послідовність n чисел впорядкованою.
Знайти суму n перших парних за номером членів геометричної прогресії з першим членом b та знаменником q.
Обчислити кількість та вивести на екран натуральні числа у проміжку 1000 - 10000, що складаються з непарних цифр.
Визначити, чи є середнє арифметичне значення всіх елементів послідовності більшим за середнє арифметичне значення найменшого та найбільшого елементів.
Щасливим називають білет, якщо сума перших трьох цифр його шестизначного номера дорівнює сумі останніх трьох цифр номера. Розв’язати задачу пошуку щасливих білетів однієї серії кількома способами та відібрати найоптимальніший з них за часом.
