Ограниченные функции

Определение 8. Функция у = f(x) называется ограниченной, если область ее значений является ограниченным множеством. Иными словами, функция у = f(x), xX, ограничена, если существует число г>0 такое, что |f(x)|<r для всех хХ.

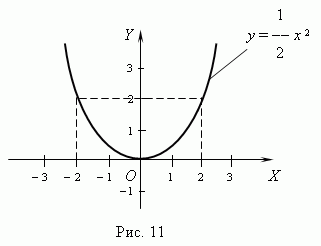
Геометрически это означает, что график функции у =f!(x) целиком лежит внутри полосы, ограниченной прямыми у= —r, у=r . Например, ограниченной является функция у=.

Иногда понятие ограниченности рассматривают в несколько более узком смысле.

Определение 9. Функция у = f(x), хХ называется ограниченной на промежутке Х₁Х, если множество значений функции на промежутке Х₁ ограничено.

Например, функция у =x²-6x+8  ограничена на отрезке [2, 4]. Во всей же области определения эта функция

не ограничена (она ограничена снизу, но не ограничена сверху).

№3

Линейная функция. Если переменные  y и x связаны уравнением 1-ой степени:

 

A x + B y = C ,

                          

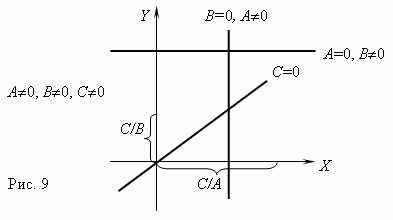
где по крайней мере одно из чисел  A  или  B  не равно нулю, то графиком этой функциональной зависимости является прямая линия. Если C = 0, то она проходит через начало координат, в противном случае - нет. Графики линейных функций для различных комбинаций A, B, C показаны на рис.9.

.

Квадратичная функция. Это функция:  y = ax 2 + bx + c, где  a, b, c - постоянные,  a  0. В простейшем случае имеем:  b = c = 0  и   y = ax 2. График этой функцииквадратная парабола - кривая, проходящая через начало координат ( рис.11 ). Каждая парабола имеет ось симметрии OY, которая называется осью параболы.Точка O пересечения параболы с её осью называется вершиной параболы.

Степенная функция. Это функция:  y = axⁿ, где  a , n – постоянные. При  n = 1 получаем прямую пропорциональность:  y = ax; при  n = 2 - квадратную параболу; при  n = 1 - обратную пропорциональность или гиперболу. Таким образом, эти функции - частные случаи степенной функции. Мы знаем, что нулевая степеньлюбого числа, отличного от нуля, равна 1, cледовательно, при  n = 0 степенная функция превращается в постоянную величину:  y = a, т.e. её график - прямая линия, параллельная оси  Х, исключая начало координат ( поясните, пожалуйста, почему ? ). 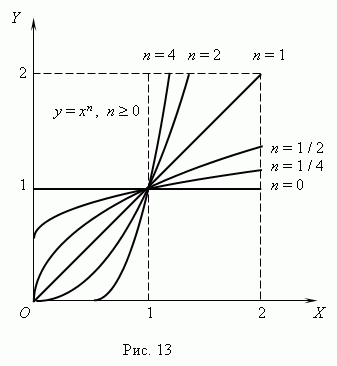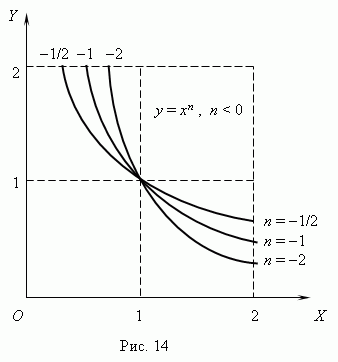Все эти случаи ( при  a = 1 ) показаны на рис.13  ( n   0 ) и рис.14 ( n< 0 ). Отрицательные значения  x здесь не рассматриваются, так как тогда некоторые функции:

Если  n – целые, степенные функции имеют смысл и при x < 0, но их графики имеют различный вид в зависимости от того, является ли  n  чётным числом или нечётным. На рис.15 показаны две такие степенные функции:  для  n = 2  и  n = 3.

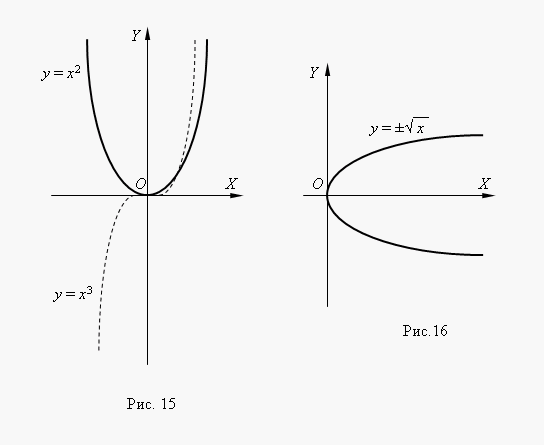
При n = 2 функция чётная и её график симметричен относительно оси Y. При n = 3 функция нечётная и её график симметричен относительно начала координат. Функция  y = x ³ называется кубической параболой.

На рис.16 представлена функция  . Эта функция является обратной к квадратной параболе  y = x ², её график получается поворотом графика квадратной параболы вокруг биссектрисы 1-го координатного углаЭто способ получения графика любой обратной функции из графика её исходной функции. Мы видим по графику, что это двузначная функция ( об этом говорит и знак    перед квадратным корнем ). Такие функции не изучаются в элементарной математике, поэтому в качестве функции мы рассматриваем обычно одну из её ветвей:  верхнюю или нижнюю.

Обратная пропорциональность. Если переменные  y  и  x обратно пропорциональны, то функциональная зависимость между ними выражается уравнением:

 

y = k / x ,

                                                 

где  k - постоянная величина.

График обратной пропорциональности – гипербола ( рис.10 ). У этой кривой две ветви. Гиперболы получаются при пересечении кругового конуса плоскостью ( оконических сечениях см. раздел «Конус» в главе «Стереометрия» ). Как показано на рис.10, произведение координат точек гиперболы есть величина постоянная,в нашем примере равная 1. В общем случае эта величина равна  k, что следует из уравнения гиперболы:  xy = k.

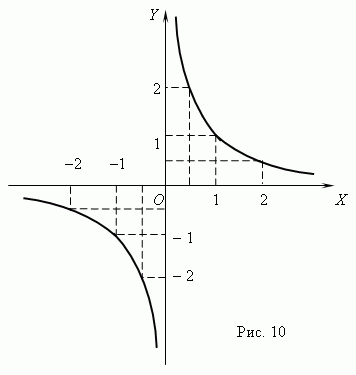
Основные характеристики и свойства гиперболы:

        - область определения функции:  x  0,  область значений:  y   0 ;

  - функция монотонная ( убывающая ) при  x < 0 и при  x > 0, но не 

 монотонная в целом из-за точки разрыва  x = 0 ( подумайте, почему ? );

  - функция неограниченная, разрывная в точке x = 0, нечётная, непериодическая;

  - нулей функция не имеет.