9.2.4. Решение задач горно-геологического профиля средствами теории вероятности и математической статистики

Теория вероятности и математическая статистика очень часто используются при решении технических задач. Но рассмотреть какие-то общие подходы к их решению, как, например, в пункте 9.2.3 в случае дифференциальных уравнений, достаточно сложно, да и не целесообразно. Подобные задачи зачастую заключаются в вычислении тех или иных характеристик случайной величины и построении ее функции распределения (теория вероятности); сборе и группировке статистического материала, а также анализ полученных статистических данных.

Рассмотрим одну из задач горно-геологического направления, связанных с теорией вероятности.

Задача. На руднике, на некотором участке находится в работе в течении смены три отбойных молотка. Вероятность выхода из строя в течении смены для одного отбойного молотка равна 0,2. Составить закон распределения числа отбойных молотков, вышедших из строя в течении смены. Найти его математическое ожидание, дисперсию и построить функцию распределения.

Решение. Рассмотрим случайную величину – число отбойных молотков, вышедших из строя в течении смены. Возможные значения 0, 1, 2, 3. Вероятности для возможных значений случайной величины будем определять по формуле Бернулли (8.4.3) из пункта 8.4.3. лекции 8.4. раздела 8.

;

;

;

.

Выполним проверку: вычислим , значит, закон составлен верно.

Запишем закон распределения в виде таблицы (табл. 9.2.1)

Таблица 9.2.1

	0	1	2	3
	0,512	0,384	0,096	0,008

Для определения математического ожидания и дисперсии нам понадобятся формулы из пункта 8.5.2. лекции 8.5. раздела 5.

.

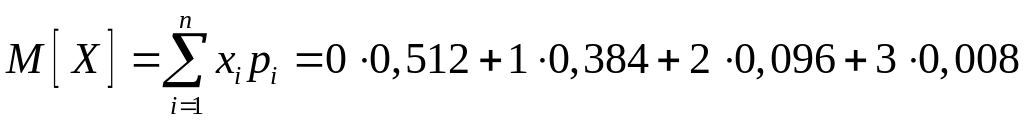Вычислим вспомогательную величину

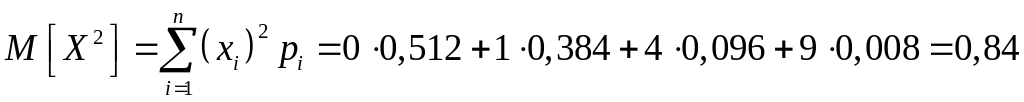
и дисперсию .

Находим функцию распределения случайной величины как указано в пункте.8.5.4. лекции 8.5. раздела 8.

Согласно определению имеем

, так как случайная величина не может принимать значение меньше 0;

;

;

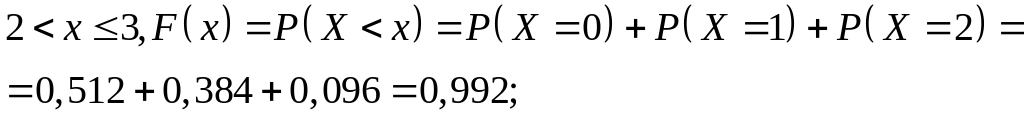
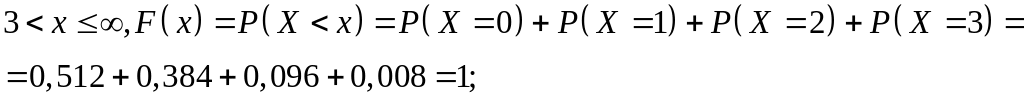
Построим график функции распределения (рис. 9.2.2).

Задача решена.

Следующая прикладная задача связана с математической статистикой. Для ее решения нам понадобится материал лекций 8.6. и 8.7. раздела 8., а также некоторые дополнительные сведения, которые мы приведем далее.

Задача. Исследовалась выработка на одного рабочего-станочника механического цеха в отчетном году в отношении к предыдущему году. Получены следующие данные (в процентах): 98, 85, 101, 118, 101, 119, 82, 102, 112, 123, 99, 104, 107, 128, 106, 87, 103, 96, 116, 129, 108, 135, 107, 116, 89, 94, 109, 113, 93, 101, 103, 99, 105, 104, 111, 121, 95, 108, 117, 106, 115, 126, 97, 103, 131, 107, 119, 139, 99, 109. Построить интервальный вариационный ряд, гистограмму. Найти выборочную среднюю, выборочную дисперсию и выборочное среднее квадратическое отклонение.

Решение. Признак – выработка в отчетном году в процентах к предыдущему может принять любое значение в некотором числовом интервале. Такой признак называют непрерывно варьирующим. Составим интервальный вариационный ряд. Определим величину интервала (шаг) по формуле Стерджеса

.

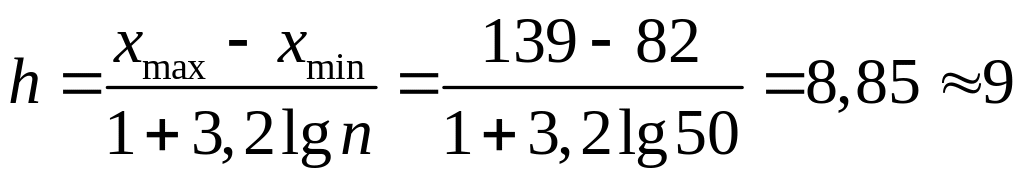Величину интервала определяем с той же точностью, как и исходные данные. Запись интервалов начинаем с до тех пор, пока не войдет . Для каждого интервала определяем частоту – число включений признака, попадающих в данный интервал. Условимся включать в интервал значения большие или равные нижней границы и меньшие верхней границы интервала. Запишем статистическое распределение признака (интервальный вариационный ряд) (табл. 9.2.2):

Таблица 9.2.2

Интервалы	82-91	91-100	100-109	109-118	118-127	127-135	135-145
Частота	4	9	17	9	6	4	1

Построим гистограмму частот (рис. 9.2.3).

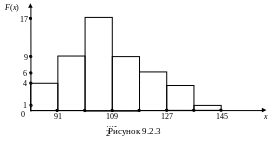
Для определения числовых характеристик перейдем к дискретному вариационному ряду (табл. 9.2.3):

Таблица 9.2.3

Середины интервалов,	86,5	95,5	104,5	113,5	122,5	131,5	140,5
Частота	4	9	17	9	6	4	1

По формуле из пункта 8.7.2. лекции 8.7. раздела 8. определяем выборочную среднюю

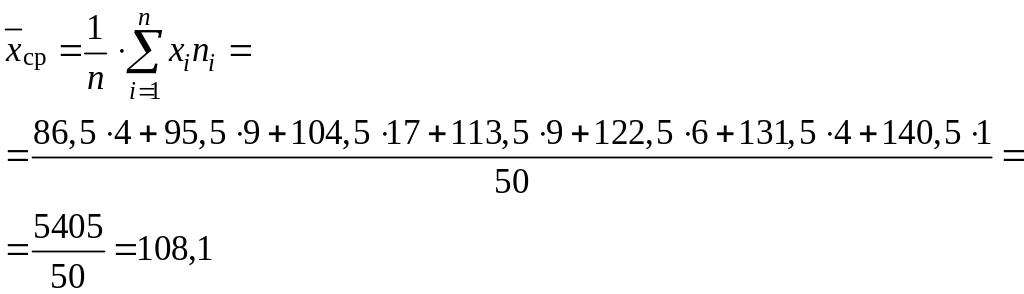
То есть средняя выработка на одного рабочего в отчетном году составляет 108,1% по отношению к предыдущему году.

Выборочную дисперсию определяем по формуле

Выборочное среднее квадратическое отклонение