
- •Раздел 9. Применение математических методов в биологии и геологии 750
- •9.1.1. Дифференциальные уравнения в математическом моделировании биологических систем
- •Лекция 9.2. Математические модели в горно-геологических задачах
- •9.2.1. Общий подход к составлению математической модели
- •9.2.2. Решение одной технической задачи
- •9.2.3. Моделирование процессов при помощи дифференциальных уравнений
- •9.2.4. Решение задач горно-геологического профиля средствами теории вероятности и математической статистики
- •Контрольные вопросы и задания для самопроверки.
9.2.3. Моделирование процессов при помощи дифференциальных уравнений
При изучении технических процессов не всегда удается непосредственно установить прямую зависимость между величинами, описывающими тот или иной процесс. Однако в большинстве случаев можно установить связь между величинами (функциями) и скоростями их изменения относительно других (независимых) переменных величин, то есть найти уравнения, в которых неизвестные функции входят под знак производной. Такие уравнения называются дифференциальными и были нами рассмотрены в разделе 4.
Опишем характер задач, приводящих к решению дифференциальных уравнений. Пусть происходит некоторый процесс, например физический, химический или биологический, и нас интересует определенная функциональная характеристика этого процесса, например закон изменения со временем температуры, давления, массы или положения тела в пространстве. Если мы обладаем достаточно полной информацией о течении этого процесса, то можно построить его математическую модель. Во многих случаях такой моделью служит дифференциальное уравнение, решением которого является искомая функциональная характеристика процесса. Дифференциальное уравнение моделирует процесс в том смысле, что оно описывает эволюцию процесса, характер изменений, происходящих с материальной системой, и возможные варианты этих изменений в зависимости от первоначального состояния системы
Но составить дифференциальное уравнение, описывающее изучаемый процесс, часто оказывается сложнее, чем решить его. Универсального метода составления математических моделей подобного рода не существует, поэтому можно дать лишь общие рекомендации.
Чтобы составить дифференциальное уравнение, необходимо выяснить, какой смысл производной используется в условии задачи.
В пункте 2.7.2. лекции 2.7. раздела 2. дается понятие геометрического и физического смысла производной.
С геометрической
точки зрения, значение производной
![]() равно угловому коэффициенту касательной,
проведенной к графику функции
равно угловому коэффициенту касательной,
проведенной к графику функции
![]() в точке с абсциссой
в точке с абсциссой
![]() .
Это так называемый геометрический смысл
производной.
.
Это так называемый геометрический смысл
производной.
С физико-механической точки зрения производная от функции – это скорость изменения одной физической величины в зависимости от изменения другой.
Если в условии задачи трудно усмотреть геометрический и физический смысл производной, то можно попытаться составить отношение приращений величин (функции и аргумента, описывающих процесс), то есть использовать определение производной:
Производной
функции одной переменной
![]() в точке
называется предел отношения приращения
функции к приращению аргумента в этой
точке, при стремлении к нулю приращения
аргумента, когда последнее произвольным
образом стремится к нулю, то есть
в точке
называется предел отношения приращения
функции к приращению аргумента в этой
точке, при стремлении к нулю приращения
аргумента, когда последнее произвольным
образом стремится к нулю, то есть
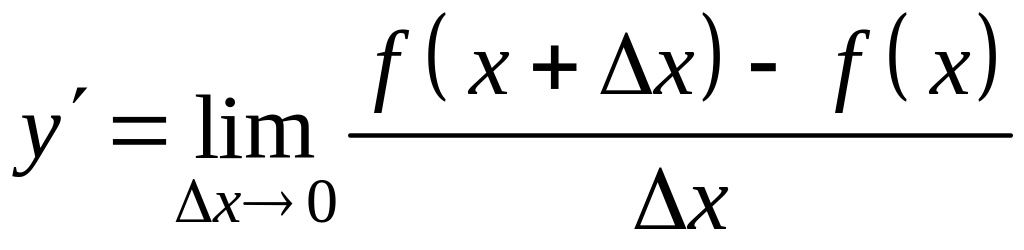 .
.
Далее можно придерживаться следующего порядка действий.
1. Определить, какую из величин принять за независимую переменную , а какую – за искомую . (При решении многих задач механики, физики, горного дела и электромеханики в роли независимой переменной выступает переменная ).
2. Установить физический или геометрический смысл функции и ее производных.
3. На основании известных законов физики, механики, электротехники и других установить зависимость между аргументом, функцией и ее производными, то есть составить дифференциальное уравнение
4. Определить тип полученного уравнения и метод его решения.
5. Решить полученное дифференциальное уравнение.
6. Если в задаче указаны начальные условия, то найти частное решение уравнения.
Рассмотрим решение задачи горно-геологического профиля, приводящей к дифференциальному уравнению второго порядка.
Задача. При движении клети в стволе очень глубокой шахты сила тяжести пропорциональна расстоянию от центра Земли. Найти время в течении которого тело пройдет заданный путь , если движение начинается с поверхности земли без начальной скорости. Сопротивлением воздуха пренебречь.
Решение.
Выберем ось вдоль ствола шахты и направим ее вертикально вниз.
Начало координат свяжем с устьем ствола.
Тогда уравнение движения клети в проекции на ось имеет вид:
![]() ,
,
где
![]() – радиус Земли;
– радиус Земли;
![]() – расстояние от клети до центра Земли;
– коэффициент пропорциональности
– расстояние от клети до центра Земли;
– коэффициент пропорциональности
![]() ;
;
![]() – ускорение свободного падения.
– ускорение свободного падения.
Подставляем в уравнение коэффициент , получим:
![]() .
.
Делим обе части уравнения на
![]() . (9.2.4)
. (9.2.4)
Получили дифференциальное уравнение второго порядка, не содержащее независимой переменной, и тем самым, допускающее понижение порядка. Более подробно такие уравнения разобраны в пункте 4.5.3. лекции 4.5. раздела 4.
Воспользуемся
заменой переменных, введем новую искомую
функцию по формуле
![]() ,
тогда уравнение (9.2.4) примет вид:
,
тогда уравнение (9.2.4) примет вид:
![]()
Это уравнение с разделяющимися переменными. Запишем его в дифференциалах
![]()
и разделим переменные:
![]() .
.
После интегрирования этого уравнения получим:
 . (9.2.5)
. (9.2.5)
Из начальных
условий:
![]() при
при
![]() ,
найдем
,
найдем
![]() .
Подставим в (9.2.5) и выразим
.
Подставим в (9.2.5) и выразим
![]() ,
получим уравнение
,
получим уравнение
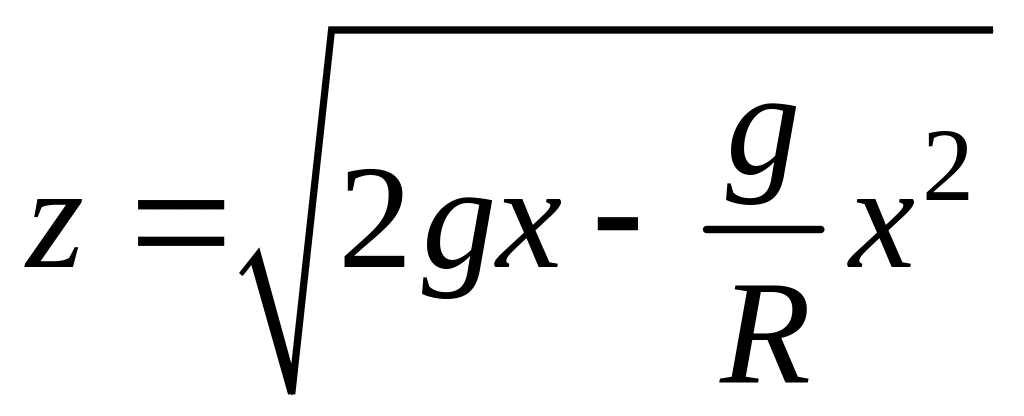 .
.
Произведем обратную замену переменных и получим уравнение
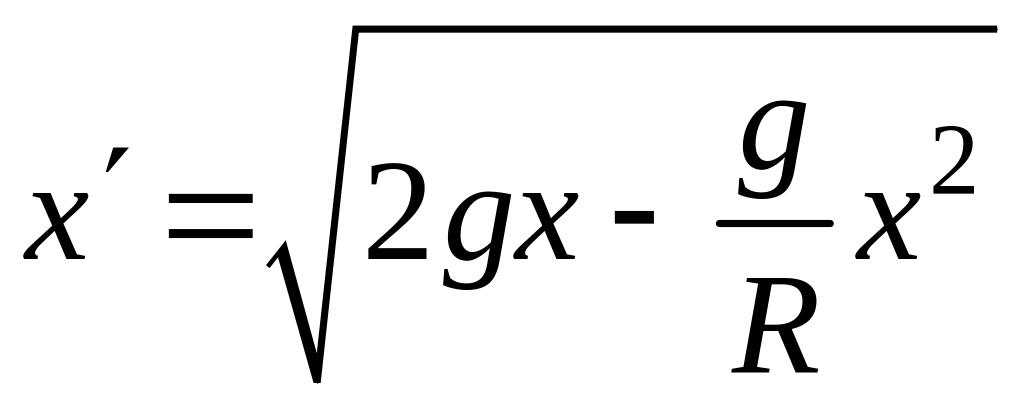 .
.
Это уравнение первого порядка с разделяющимися переменными. Запишем его в дифференциалах
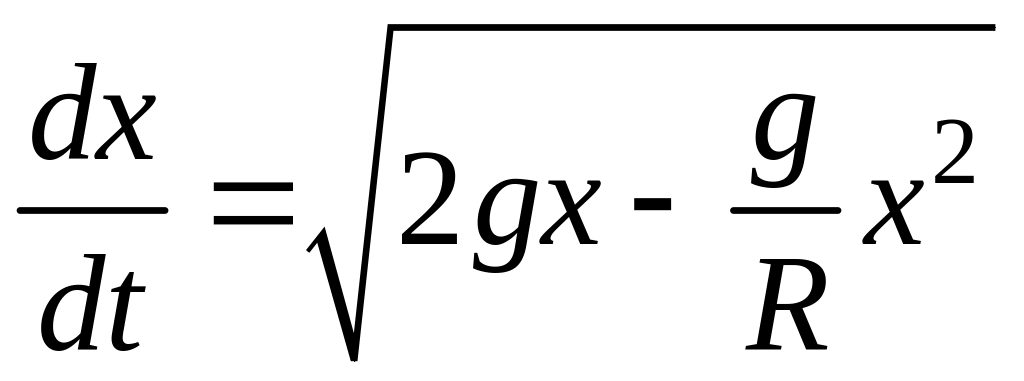
и разделим переменные:
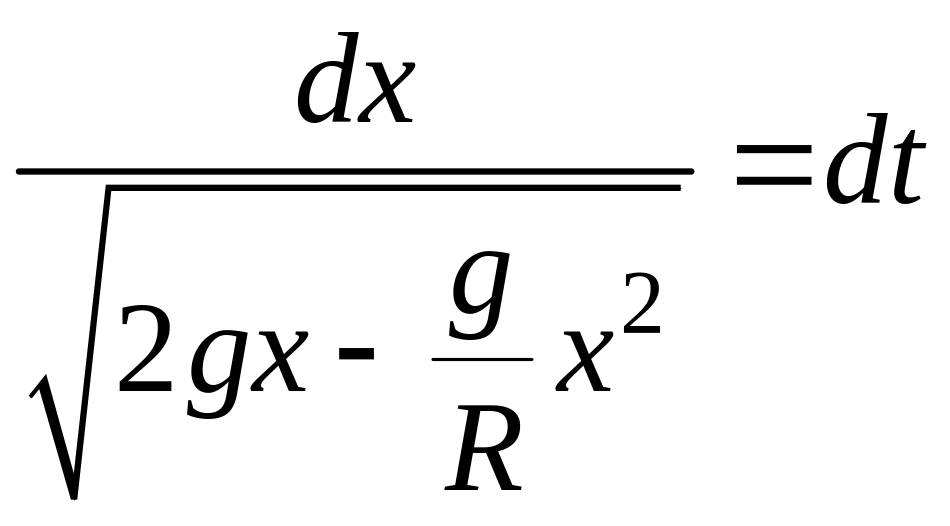 .
.
После интегрирования и проверки начальных условий получим
 .
.
Задача решена.
