
- •Раздел 7. Функции комплексного переменного. Элементы функционального анализа. 623
- •7.1.1. Основные понятия
- •7.1.2 Предел и непрерывность функции комплексного переменного
- •7.1.3. Основные элементарные функции комплексного переменного
- •7.1.3.1. Показательная функция
- •7.1.3.2. Логарифмическая функция
- •7.1.3.3. Степенная функция
- •7.1.3.4. Тригонометрические функции
- •7.1.3.5. Гиперболические функции
- •7.1.3.6. Обратные тригонометрические и гиперболические функции
- •7.1.4. Условия Коши – Римана
- •7.1.5. Аналитическая функция. Дифференциал
- •7.1.6. Интегрирование функции комплексного переменного
- •7.1.7. Интегральная формула Коши
- •7.1.8. Ряды Тейлора и Лорана
- •7.1.9. Изолированные особые точки
- •7.1.10. Вычеты
- •7.1.11. Вычисление вычетов
- •7.2.1. Метрические пространства
- •7.2.2. Примеры метрических пространств
- •7.2.3. Шары в метрическом пространстве
- •7.2.4. Полнота и пополнение метрических пространств
- •7.2.5. Принцип сжатых отображений
- •7.2.6. Применение принципа сжатых отображений
- •7.2.7 Линейные пространства
- •6. Пусть e - совокупность последовательностей таких, что .
- •7.2.8. Норма и скалярное произведение
- •7.2.9 Гильбертово пространство
- •Контрольные вопросы и задания для самопроверки
7.1.6. Интегрирование функции комплексного переменного
Пусть
– функция комплексного переменного z,
определенная в некоторой области и L
– кусочно-гладкая кривая, лежащая в
этой области. Разобьем эту кривую на n
частей
![]() точками
точками
![]() ,
пронумерованными в направлении от
,
пронумерованными в направлении от
![]() - начальной точки кривой L,
до
- начальной точки кривой L,
до
![]() - конечной точки L
(рис. 7.1.3), и на каждой части выберем
какую-нибудь точку
- конечной точки L
(рис. 7.1.3), и на каждой части выберем
какую-нибудь точку
![]() (k=1,2,…,n).
(k=1,2,…,n).
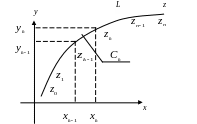
Рис. 7.1.3
Предел такой интегральной суммы при стремлении к нулю длины наибольшей из элементарных дуг, называется интегралом от функции по контуру L.
Определение 15. Интегралом от функции по кривой L называется предел
![]() , (7.1.7)
, (7.1.7)
если этот предел
существует и не зависит от выбора
промежуточных точек
![]() и
и
![]() .
.
Покажем, что если L –гладкая кривая, а функция непрерывная и однозначная, то интеграл (7.1.7) существует.
Действительно,
пусть
=u(x,y)+iv(x,y),
z=x+iy,
![]() .
Тогда
.
Тогда
![]() ,
,
![]() .
.
Поэтому
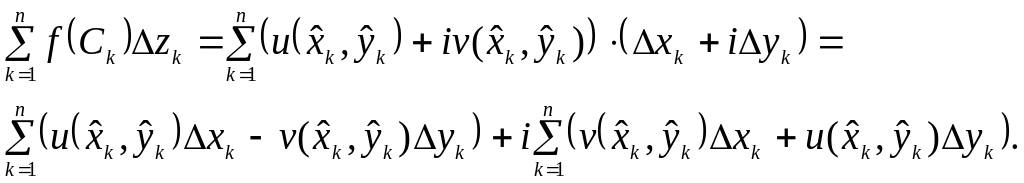
Обе суммы, находящиеся в правой части последнего равенства, являются интегральными суммами для соответствующих криволинейных интегралов.
При сделанных
предположениях о кривой L
и функции
пределы этих сумм существуют. Поэтому
после перехода к пределу в последнем
равенстве при
![]() получим:
получим:
![]() (7.1.8)
(7.1.8)
Формула (7.1.8) показывает, что вычисление интеграла от функции комплексного переменного сводится к вычислению криволинейных интегралов от действительных функций действительных переменных.
Если кривая L задана комплексным параметрическим уравнением
![]()
и учитывая, что
![]() ,
,
то формула (7.1.8) преобразуется в формулу
![]() .
.
Приведем основные свойства интеграла от функции комплексного переменного.
1.
![]() .
.
Доказательство:
![]() .
.
2.
![]() .
.
3.
![]() ,
где а
– комплексное число.
,
где а
– комплексное число.
4.
![]() ,
т.е. при перемене направления пути
интегрирования интеграл изменяет свой
знак на противоположный.
,
т.е. при перемене направления пути
интегрирования интеграл изменяет свой
знак на противоположный.
5.
![]() ,
где
,
где
![]() ,
т.е. интеграл по всему пути L
равен сумме интегралов по его частям
,
т.е. интеграл по всему пути L
равен сумме интегралов по его частям
![]() и
и
![]() .
.
6. Оценка модуля
интеграла. Если
![]() во всех точках кривой L,
то
во всех точках кривой L,
то
![]() ,
,
где l – длина кривой L.
Действительно,
![]() ,
,
где
![]() - длина ломаной
- длина ломаной
![]() ,
вписанной в кривую L.
,
вписанной в кривую L.
Теорема 3 (Теорема Коши). Если функция аналитична в некоторой односвязной области D, то интеграл от по любому замкнутому контуру L, лежащему в области D, равен нулю, т.е.
![]()
Доказательство. Докажем теорему, предполагая непрерывность производной . По формуле (7.2.3) имеем:
![]()
В силу аналитичности =u+iv и непрерывности в односвязной области D, функции u=u(x,y) и v=v(x,y) непрерывны и дифференцируемы в этой области и удовлетворяют условиям Коши-Римана:
![]() и
и
![]() .
.
Эти условия означают
равенство нулю интегралов
![]() и
и
![]() .
Следовательно,
.
Следовательно,
![]()
Теорема Коши допускает распространение на случай многосвязной области.
Следствие. Если функция аналитична в односвязной области D, то интеграл от нее не зависит от формы пути интегрирования, а зависит лишь от начальной точки и конечной точки z пути интегрирования.
Доказательство. Действительно, пусть и - две кривые в области D, соединяющие точки и z.
По теореме Коши
![]() ,
т.е.
,
т.е.
![]() или
или
![]() ,
откуда
,
откуда
![]() .
.
В таких случаях, когда интеграл зависит только от начальной точки и конечной точки пути интегрирования, будем пользоваться обозначением
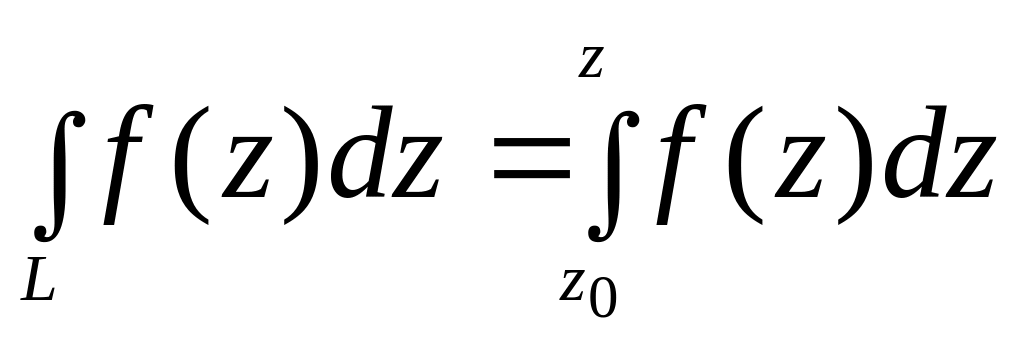 .
.
Если здесь
зафиксировать точку
,
а точку z
изменять, то
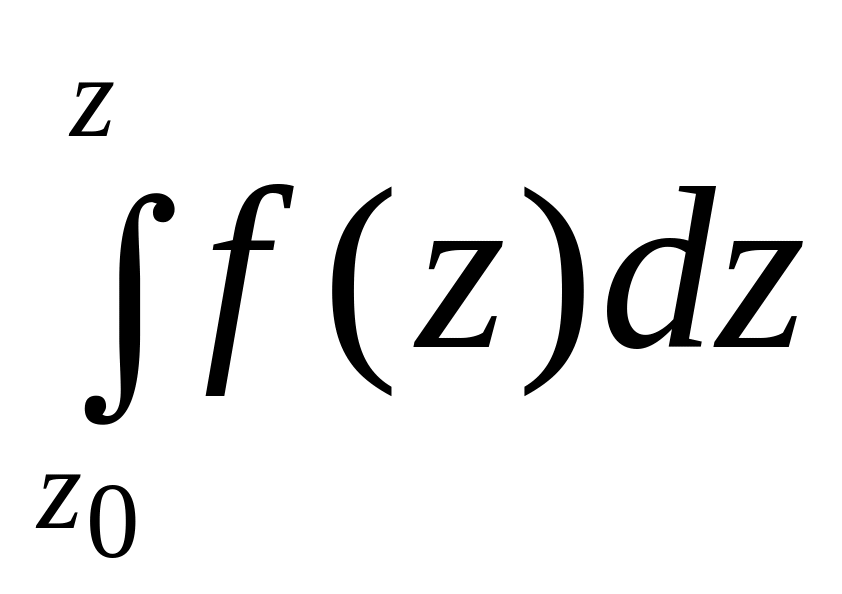 будет функцией от z.
Обозначим эту функцию через F(z):
будет функцией от z.
Обозначим эту функцию через F(z):
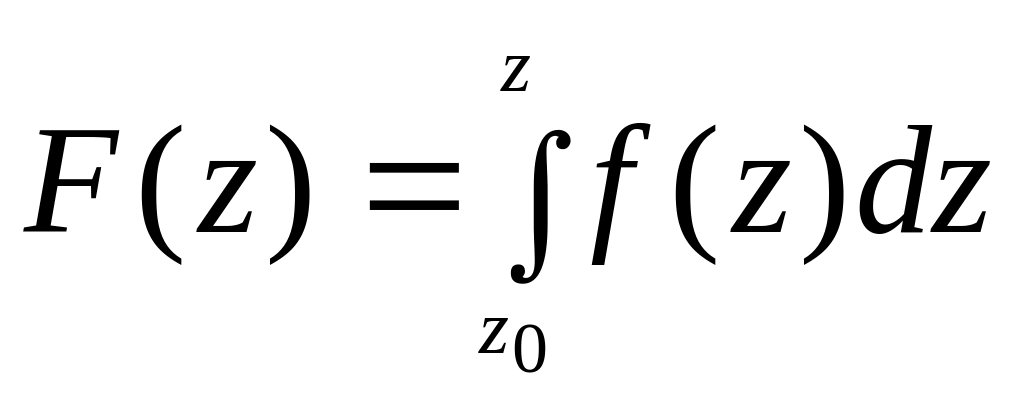 .
Можно доказать, что если функция
аналитична в односвязной области D,
то функция F(z)
также аналитична в D,
причем
.
Можно доказать, что если функция
аналитична в односвязной области D,
то функция F(z)
также аналитична в D,
причем
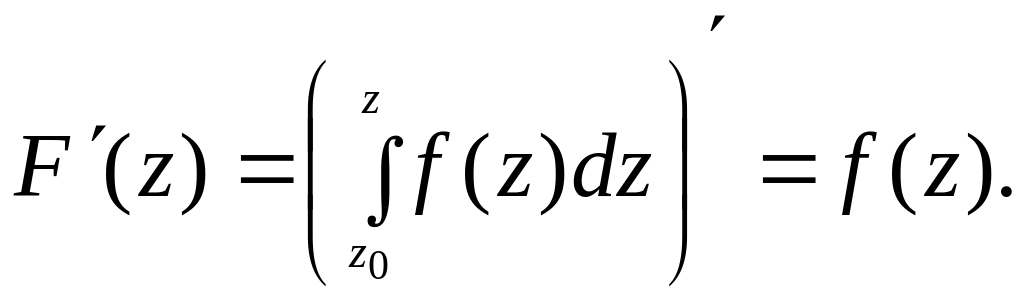
Определение 16.
Функция F(z)
называется первообразной
для функции
в области D,
если
![]() .
.
Можно показать, что если F(z) есть некоторая первообразная для , то совокупность всех первообразных определяется формулой F(z)+C, где С =const.
Определение 17.
Совокупность всех первообразных функции
называется неопределенным
интегралом
от функции
и обозначается символом
![]() ,
т.е.
,
т.е.
![]() где
где
![]()
Как и в вещественном анализе, для функции комплексного переменного справедлива формула Ньютона-Лейбница:
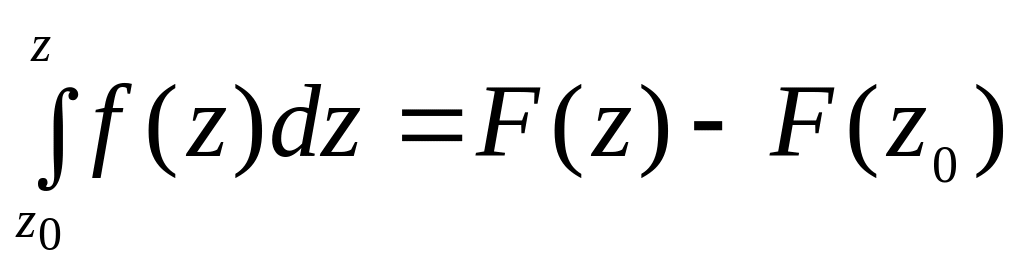 .
.
Пример 6.
Вычислить интеграл
![]() ,
где L:
,
где L:
1) отрезок прямой от точки 0 до точки 1+2i;
2) дуга параболы
![]() от точки 0 до точки 1+2i.
от точки 0 до точки 1+2i.
Решение.
1) так как L
– отрезок прямой
![]() и
и
![]() ,
то
,
то
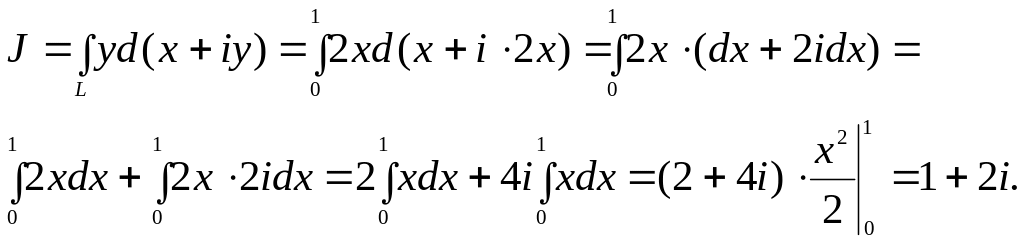
так как для всех точек L имеем , то
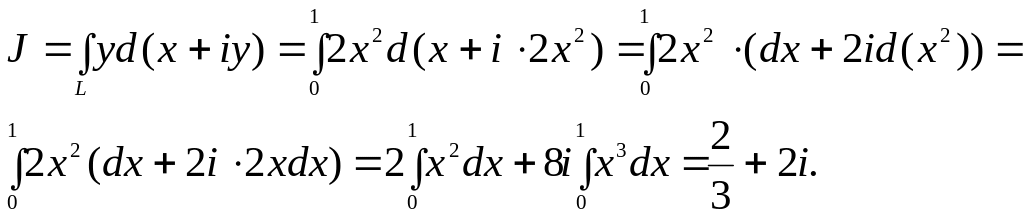
Этот пример
показывает, что если L
– кривая в области D
с начальной точкой
и конечной точкой
![]() ,
а
не аналитическая функция в D,
то интеграл
,
а
не аналитическая функция в D,
то интеграл
![]() ,
вообще говоря, зависит не только от
точек
и
,
а также и от вида кривой L.
,
вообще говоря, зависит не только от
точек
и
,
а также и от вида кривой L.
