7.2.5. Принцип сжатых отображений

Теорема 6 (принцип вложенных шаров). Метрическое пространство X является полным тогда и только тогда, когда любая последовательность вложенных друг в друга замкнутых шаров, диаметры которых стремятся к нулю, имеет непустое пересечение.

Замечание. В формулировке теоремы все условия (замкнутость шаров, полнота пространства, вложенность шаров, стремление к нулю) являются существенными.

Определение 9. Отображение называется непрерывным, если из того, что последовательность следует, что .

Определение 10. Отображение называется сжимающим, если существует число такое, что выполнено

,

при этом коэффициент q называется коэффициентом сжатия отображения.

Определение 11. Точка x называется неподвижной точкой отображения , если .

Теорема 7 (о сжимающем отображении). Всякое сжимающее отображение F полного метрического пространства в себя обладает единственной неподвижной точкой x, при этом, для любого последовательность итераций

, , ,…,

сходится к точке x, причем имеет место следующая оценка скорости сходимости:

.

Полнота пространства может оказаться необходимой при решении уравнений .

Действительно, если решать эти уравнения методом последовательных приближений, в случае неполноты пространства при переходе к переделу, мы можем получить элемент, не удовлетворяющий нашему уравнению. Так, например, при решении дифференциального уравнения в пространстве методом последовательных приближений, предельный элемент может оказаться недифференцируемой функцией и, следовательно, не будет удовлетворять нашему дифференциальному уравнению.

Сделаем некоторые замечания о пополнении метрических пространств.

Полнота вещественной прямой играет большую роль в математическом анализе. При этом множество вещественных чисел является пополнением множества рациональных чисел, причем таким, что расстояние между элементами при пополнении сохраняются. Поэтому становится естественной постановка задачи аналогичного пополнения неполных метрических пространств. Для более точной формулировки этой задачи введем некоторые определения.

Определение 12. Метрические пространства и Y называются изометрическими, если между ними можно установить такое взаимно – однозначное соответствие, что расстояние между прообразами и в равно расстоянию между образами и в Y, т. е.

.

Определение 13. Множество M называется плотным в множестве G, если его замыкание содержит G, т.е. .

Определение 14. Множество M всюду плотно в пространстве , если .

Имеет место утверждение о пополнении метрических пространств:

Теорема 8. Пусть - неполное метрическое пространство. Тогда существует такое полное метрическое пространство , в котором содержится подпространство , всюду плотное в и изометричное пространству .

Пространство называется пополнением пространства .

Пример 2. Покажем, что пространство P заданных на отрезке алгебраических полиномов

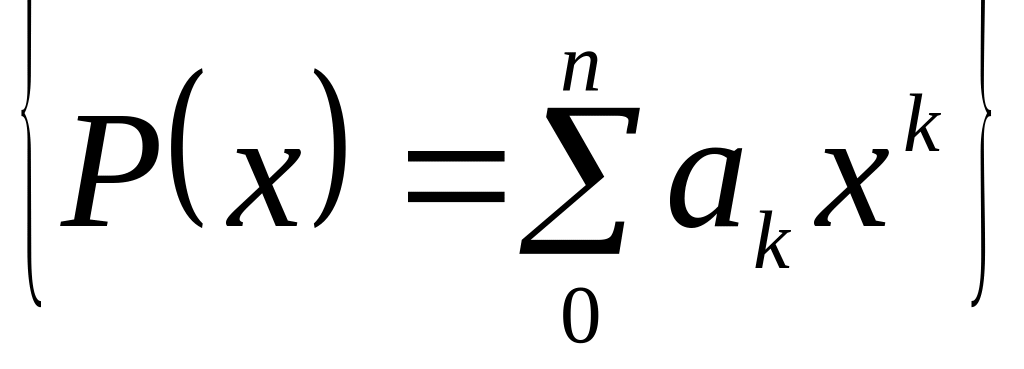
с метрикой не является полным.

Для этого рассмотрим последовательность полиномов: ,

Предел этой последовательности, функция , не принадлежит P. Из теоремы Вейерштрасса следует, что пространство P всюду плотное в пространстве непрерывных функций , а это означает, что пространство можно рассматривать как пополнение пространства P.

Теорема 9 (о пополнении). Любое метрическое пространство допускает пополнение, единственное с точностью до изометрии.

Большое применение в математическом анализе, теорий дифференциальных и интегральных уравнений, а также в линейной алгебре имеет принцип сжатых отображений, сущность которого рассмотрим на примерах.

Пример 3. На числовой прямой дан отрезок. Проведем его сжатие. Это значит, что его концы переместятся в новые точки

Точки, ранее занимавшие положение , переместятся в точки и т. д. Интуитивно можно предположить, что на отрезке существует точка С, которая при его сжатии останется неподвижной. Точнее говоря, отрезок лежит на числовой прямой. Каждой точке х, принадлежащей отрезку , поставим в соответствие некоторую точку , которая является отображением точки х. Неподвижная точка, если она существует, удовлетворяет равенству .

Пример 4. Пусть на отрезке задано множество Е функций таких, что , где , M - некоторое заданное положительное число. Функцию будем называть «точкой» множества Е.

Если каждой точке поставлена в соответствие некоторая точка того же множества, то считается, что задано отображение множества Е на себя. Например, пусть на отрезке задано множество Е функций : Поставим функции в соответствие функцию . Тогда .

Заметим, что для доказательства существования решений алгебраических, дифференциальных, интегральных уравнений и систем таких уравнений, а также для отыскания решений этих уравнений применяется метод последовательных приближений. Принцип сжатых отображений представляет такое обобщение метода последовательных приближений, с помощью которого исследуется общее (операторное) уравнение

(7.2.4)

и изучается общее уравнение метрического пространства, и, таким образом, изучение уравнений различного класса укладывается в единую общую схему. Для уравнения , взяв любой элемент , строим последовательность приближенных решений уравнения . Если существует предел этой последовательности , этот предел удовлетворяет уравнению (7.2.4) и сходится к решению этого уравнения.