Лекция 4.4. Уравнения в полных дифференциалах. Уравнения высших порядков. Основные понятия и определения.

4.4.1. Уравнения в полных дифференциалах

Определение 1. Уравнение

M(x, y) dx + N(x, y) dy = 0, (4.4.1)

левая часть которого представляет собою полный дифференциал некоторой функции U от x и y, т. е.

M(x, y) dx + N(x, y) dy = dU (4.4.2)

называется уравнением в полных дифференциалах.

Относительно функций M и N мы будем предполагать, что они непрерывны по обеим переменным в некоторой односвязной области и ни в одной точке этой области не обращаются одновременно в нуль.

Уравнение в полных дифференциалах можно записать так:

dU = 0. (4.4.3)

Поэтому общий интеграл его имеет вид

U(x,y)=C. (4.4.4)

При этом функция U является интегралом уравнения (4.4.1). Особых решений уравнение в полных дифференциалах, очевидно, не имеет.

Поэтому возникают два вопроса: 1) как узнать по виду уравнения (4.4.1), является ли оно уравнением в полных дифференциалах? 2) В случае положительного ответа на первый вопрос, как построить функцию U и, следовательно, общий интеграл уравнения (4.4.1)?

Предположим, что функции M(x,y) и N(x,y) имеют непрерывные частные производные соответственно по y и по x. Пусть левая часть уравнения (4.4.1) представляет собою полный дифференциал, т. е.

.

Это равносильно тому, что имеют место тождества

. (4.4.5)

Дифференцируя первое из этих тождеств по y, а второе по x, получаем тождества:

; (4.4.6)

левые части полученных тождеств равны между собою, а тогда равны и правые, т. е.

. (4.4.7)

Условие (4.4.7) является необходимым для того, чтобы левая часть уравнения (4.4.1) была полным дифференциалом. Покажем, что это условие является достаточным, если область односвязна. Действительно, пусть условие (4.4.6) выполнено. Покажем, что тогда существует функция U, удовлетворяющая соотношению (4.4.2) или, равенствам (4.4.5).

Будем исходить из первого из равенств (4.4.5):

. (4.4.8)

Нетрудно убедиться, что ему удовлетворяет функция

, (4.4.9)

где  (y) – произвольная функция от y, которую мы будем считать дифференцируемой и выберем ее так, чтобы функции (4.4.9) удовлетворяла и второму из равенств (4.4.5), т. е. чтобы

(4.4.10)

или

(4.4.11)

Используя условие (4.4.7), перепишем это равенство так:

(4.4.12)

Выполняя интегрирование, получаем:

N(x,y)  N(x₀,y) + (y) = N(x,y)

откуда

(y) = N(x₀,y),

следовательно

(4.4.13)

где C – уже произвольная постоянная. Подставляя найденное выражение функции  (y) в формулу (4.4.9), получаем искомую функцию U(x, y):

, (4.4.14)

что и доказывает достаточность условия (4.4.7). Итак, тождественное выполнение равенства (4.4.7) является необходимым и достаточным признаком уравнения в полных дифференциалах.

Взяв одну из функций, например, ту, в которой C = 0, и приравняв ее произвольной постоянной С, получим общий интеграл уравнения (4.4.1) в следующем виде:

. (4.4.15)

Если при построении функции U брать за исходное второе из равенств (4.4.5), то мы получим для общего интеграла следующее выражение:

. (4.4.16)

В формулах (4.4.15) и (4.4.16) нижние пределы интегрирования x₀ и y₀ можно выбирать произвольно в пределах рассматриваемой односвязной области, но так, чтобы получающиеся интегралы имели смысл. Удачный выбор x₀ и y₀ во многих случаях облегчает задачу интегрирования уравнения.

Пример 1. Рассмотрим уравнение

(x³+y)dx+(xy)dy=0.

Здесь M= x³+y, N= xy, , , так что условие (4.4.7) выполнено. Для получения общего интеграла воспользуемся формулой (4.4.15), где положом x₀=y₀=0, тогда получим

Интегрируя получим общий интеграл в виде .

Пример 2. Дано уравнение

Условие (4.4.7) выполнено. Применим формулу (4.4.15), положив x₀=0, y₀=1. Получим:

.

Формулы (4.4.15) и (4.4.16) дают возможность легко получить решение задачи Коши с начальными даннымй x₀, y₀, если точка (x₀, y₀) лежит в указанной выше области.

Достаточно взять в качестве нижних пределов эти начальные данные и положить C = 0. Получим две формулы:

, (4.4.17)

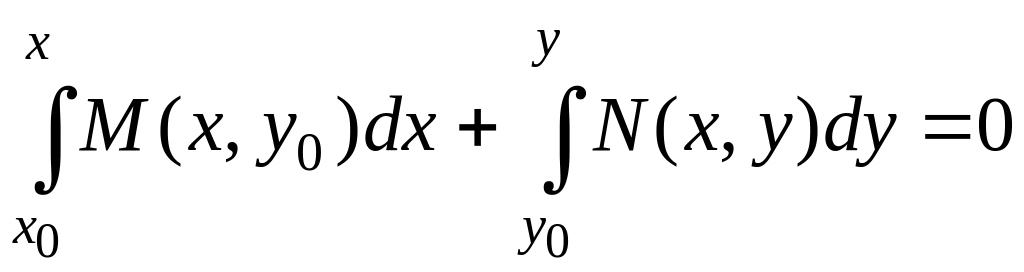, (4.4.18)

которые и определяют (каждая в отдельности) искомое решение задачи Коши. Оно будет единственным.