4.2.5. Простейшее уравнение, приводящееся к однородному

Рассмотрим уравнение

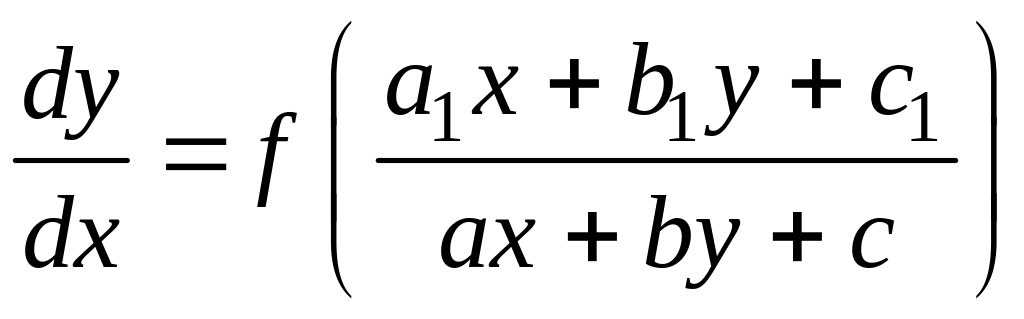. (4.2.32)

Если c₁=c=0, то это уравнение однородное, ибо оно приводится к виду (4.2.24). Пусть хоть одно из чисел c₁, c отлично от нуля и предположим еще, что

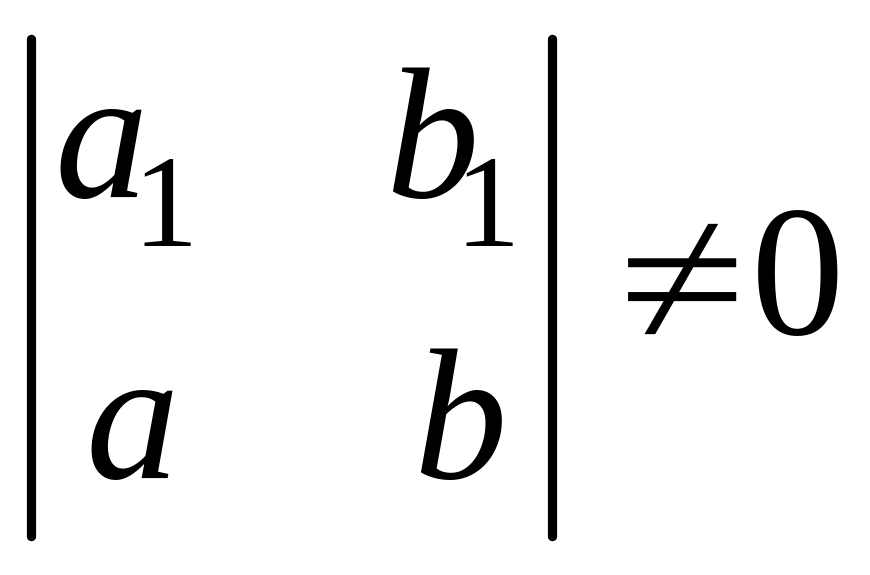. (4.2.33)

Сделаем линейную замену обеих переменных:

x=, y=. (4.2.34)

Тогда наше уравнение примет вид

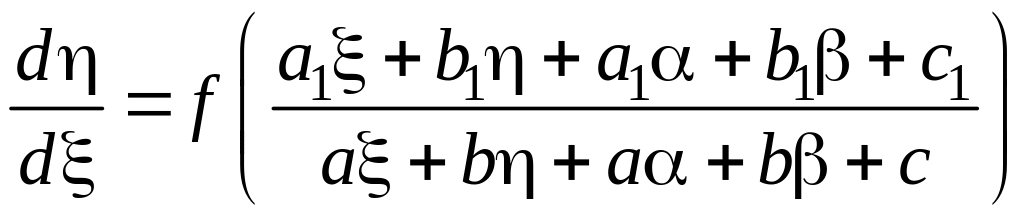
Выбрав  и  так, чтобы

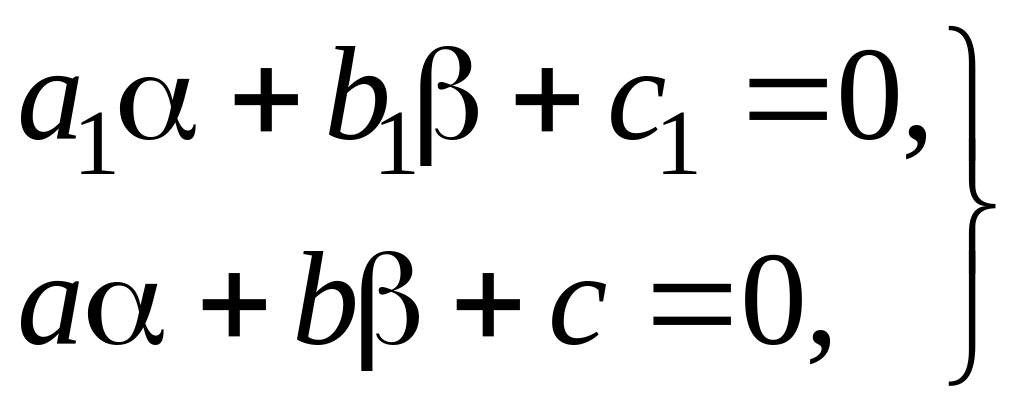
получим однородное уравнение

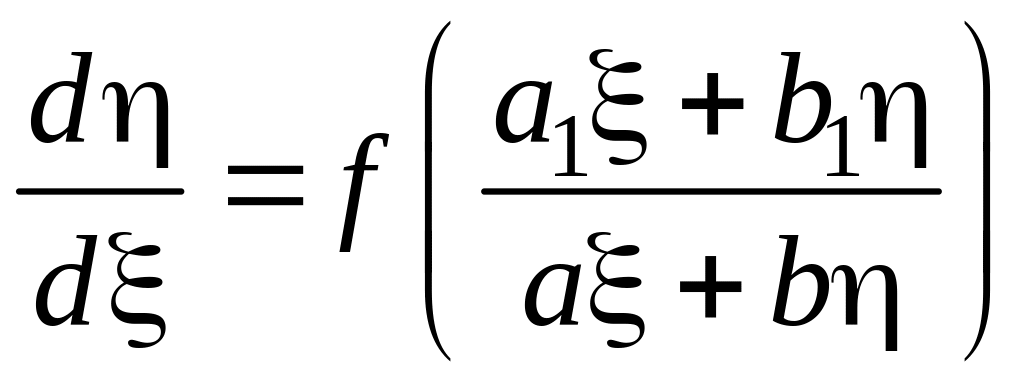(4.2.35)

Интегрируя его и возвращаясь к переменным x и y, найдем общий интеграл уравнения (4.2.32).

Если же 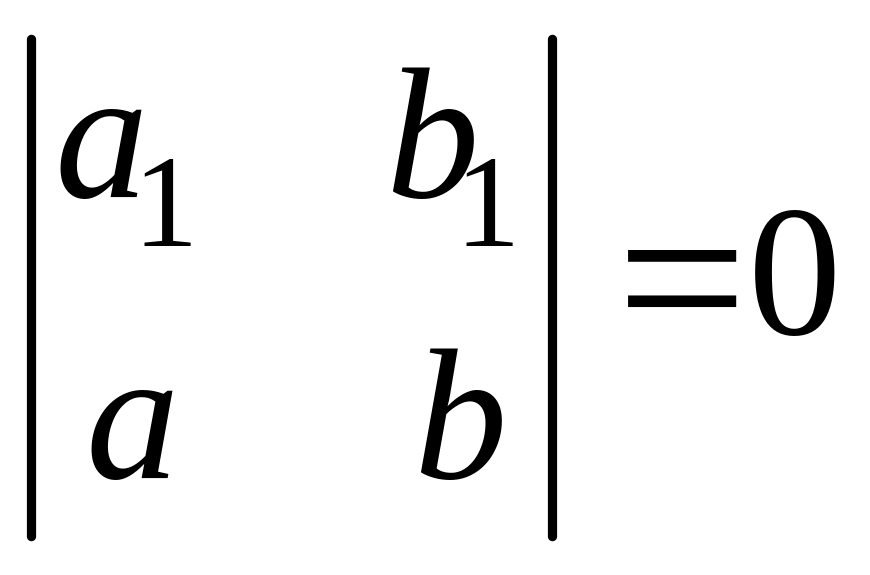то мы имеем , откуда a_l=ka, b₁=kb. Поэтому уравнение (4.2.32) можно переписать в этом случае так:

. (4.2.32)

Введя здесь вместо y новую неизвестную функцию z по формуле z=ax+by, мы придем к уравнению, не содержащему независимой переменной:

. (4.2.36)

Лекция 4.3. Линейное уравнение первого порядка. Метод вариации произвольной постоянной (метод лагранжа). Уравнение бернулли

4.3.1. Линейное уравнение

Определение 1. Уравнение вида

(4.3.1)

называется линейным. Оно содержит искомую функцию y и ее производную y только в первой степени. Если записать его в виде, разрешенном относительно производной, то получим уравнение

, (4.3.2)

правая часть которого есть линейная функция от y с коэффициентами, зависящими от x (которые, в частности, могут быть и постоянными).

Относительно функций p(x) и q(x) будем предполагать, что они непрерывны в интервале (a, b) (a, b +).

Определение 2. Если в уравнении (4.3.1) функция q(x) тождественно равна нулю во всем интервале (a, b), то это уравнение принимает вид

(4.3.3)

и называется однородным. Его левая часть есть однородная линейная функция от y и y. Уравнение (4.3.1), в котором , называется неоднородным.

Уравнение вида

, (4.3.4)

в котором коэффициент при y не равен единице, также называется линейным. Если p₀(x), p₁(x) и q(x) непрерывны в интервале (a, b), причем p₀(x) не обращается (в этом интервале)в нуль, то уравнение (4.3.4), делением обеих частей его на p₀(x), приводится к уравнению вида (4.3.1), в котором коэффициент при искомой функции и правая часть непрерывны в интервале (a, b).

Из теоремы Пикара о достаточном условии существования и единственности решения задачи Коши, сформулированной ранее, следует, что при сделанных предположениях относительно p(x) и q(x) уравнение (4.3.1) имеет единственное решение

y=y(x) (4.3.5)

удовлетворяющее начальному условию:

y = y₀ при x =x₀ (4.3.6)

где в качестве x₀ можно брать любое число из интервала (a, b), а y₀ можно выбирать произвольно, т. е. через любую точку M₀(x₀,y₀) полосы

a< x <b, <y< + (4.3.7)

проходит одна и только одна интегральная кривая уравнения (4.3.1).

В самом деле, если записать уравнение (4.3.1) в виде:

, (4.3.8)

то ясно, что можно построить такой прямоугольник

R:

с центром в точке (x₀,y₀), целиком содержащийся внутри полосы (4.3.7), что внутри него правая часть уравнения (4.3.8) будет удовлетворять обоим условиям теоремы Пикара, ибо в этом прямоугольнике f(x,y) непрерывна и ограничена, а 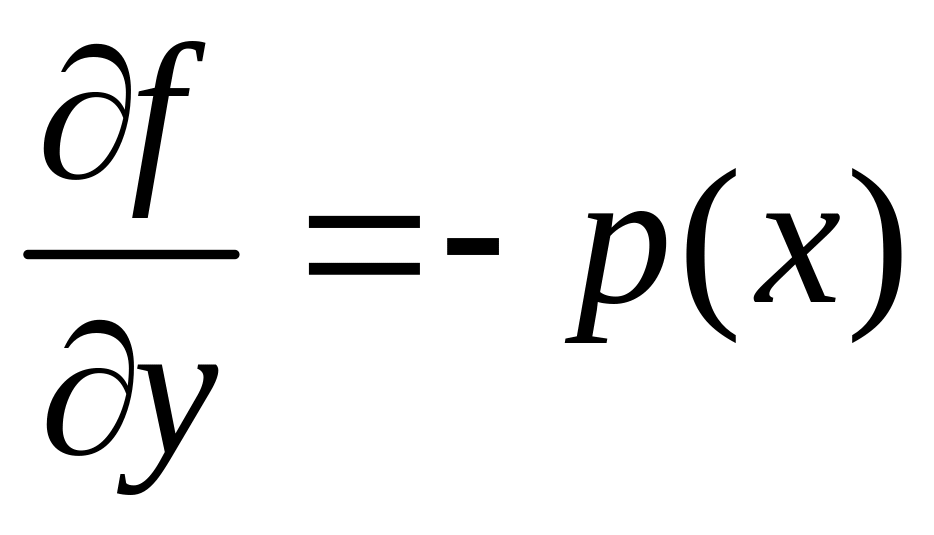, так что существует и ограничена. А тогда уравнение (4.3.8) или, что то же, уравнение (4.3.1) имеет одно и только одно решение с начальными данными x₀, y₀. Это решение непрерывно дифференцируемо. Всякое решение линейного уравнения (4.3.1) есть частное решение, так как во всей области задания этого уравнения, т. е. во всей полосе (4.3.7), имеет место существование и единственность решения задачи Коши. Линейное уравнение (4.3.1) при сделанных предположениях не имеет особых решений.

Прежде чем перейти к интегрированию линейного уравнения, отметим два общих свойства этого уравнения.

1. Линейное уравнение сохраняет свой вид (т. е. остается линейным) при любой замене независимой переменной

x=(t), (4.3.9)

где (t) – любая функция от t, определенная и непрерывно дифференцируемая в интервале (t₀, t₁), причем a=(t₀), b=(t₁). (t)  0 во всем интервале (t₀,t₁). В самом деле, мы имеем:

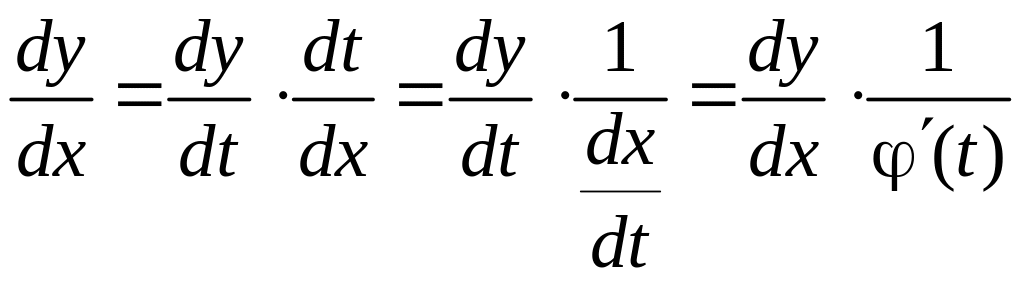(4.3.10)

Поэтому, подставляя x = (t) в (4.3.1), получим линейное уравнение

, (4.3.11)

причем его коэффициент при y и правая часть непрерывны в интервале (t₀,t₁).

2. Линейное уравнение сохраняет свой вид при любой линейной замене искомой функции

y = (x) z + (x),

где z – новая неизвестная функция, а (x) и (x) – произвольные непрерывно дифференцируемые функции от x, причем (x)  0 в (a,b). Действительно, так как

y=(x)z+(x)z+(x) (4.3.12)

то после преобразования получим

(x)z+(x)z+(x)+p(x)[(x) z + (x)]=q(x)

или

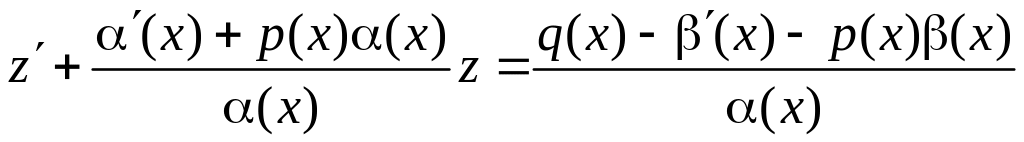, (4.3.13)

т. е. опять линейное уравнение, у которого коэффициент при искомой функции и правая часть непрерывны в (a, b).

Заметим, что если  (x) обращается в нуль в некоторых точках интервала (a, b), то преобразованное уравнение будет тоже линейным, но коэффициент при искомой функции и правая часть могут иметь разрыв в этих точках.

Покажем, что линейное уравнение всегда интегрируется в квадратурах. Рассмотрим сначала однородное линейное уравнение (4.3.3)

где функция p(x) непрерывна в интервале (a, b). Переписав это уравнение в виде

(4.3.14)

получаем уравнение с разделяющимися переменными. Разделяя переменные, получим:

,

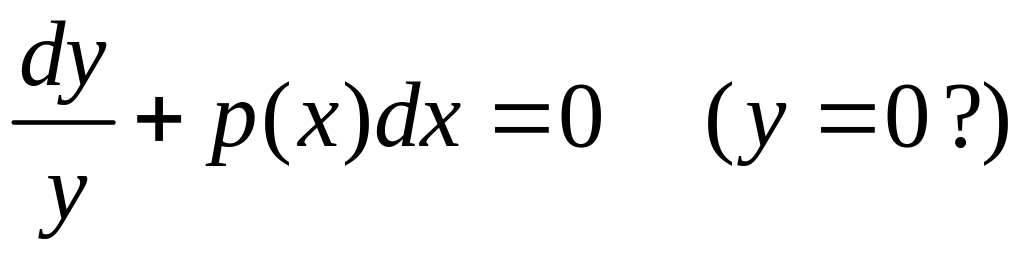откуда

, (4.3.15)

где C – произвольная постоянная.

Все решения уравнения (4.3.3) содержатся в формуле (4.3.15), так как разделяя переменные, мы могли потерять лишь очевидное нулевое решение y = 0, но и оно содержится в (4.3.15) при C = 0. Из формулы (4.3.15) видно, что всякое решение уравнения (4.3.3) определено во всем интервале (a, b).

Покажем, что функция (4.3.15) является общим решением уравнения (4.3.3) в области (4.3.7), т. е. во всей области задания уравнения (4.3.3).

В самом деле (4.3.15) разрешимо относительно C в области (4.3.7), так что мы имеем:

,

где функция справа определена в области (4.3.7). Кроме того, по построению функция (4.3.15) является решением уравнения (4.3.3) в интервале (a, b) при всех значениях произвольной постоянной C. А это и означает, что функция (4.3.15) есть общее решение уравнения (4.3.3) в области (4.3.7).

Пример 1. Рассмотрим уравнение

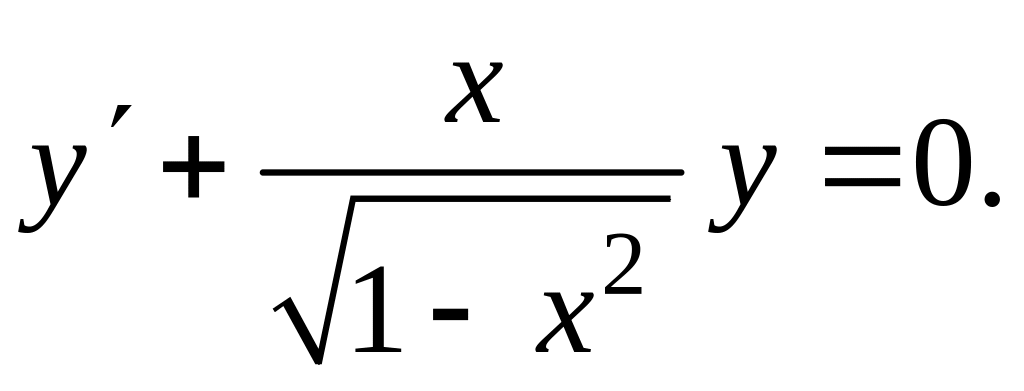
Здесь коэффициент 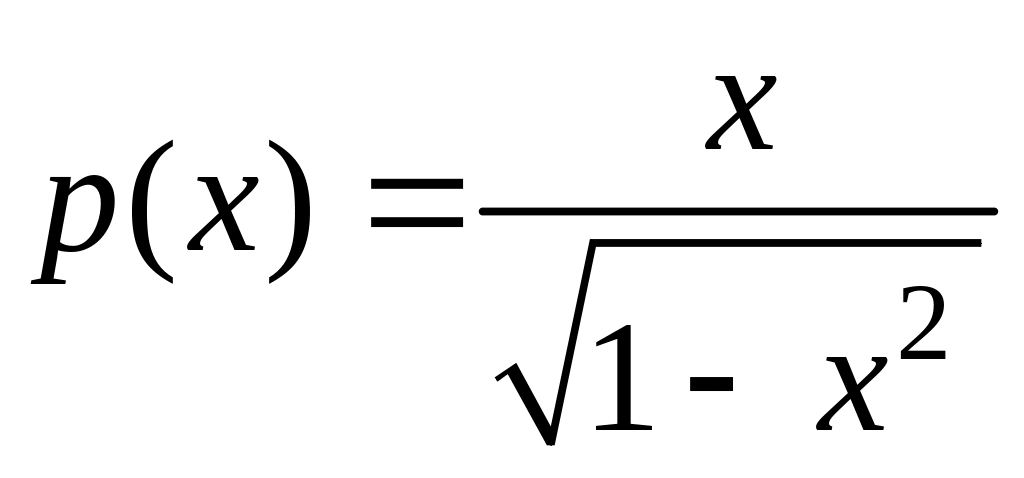есть функция, определенная и непрерывная в интервале (1,+1). Пользуясь формулой (4.3.15), найдем:

.

Это есть общее решение рассматриваемого уравнения в области:

1<x<+1, <y<.

Пример 2. Найти решение уравнения:

y+2xy=0.

В этом случае p(x)=2x не имеет точек разрыва. Поэтому всякое решение определено при всех x. Действительно, интегрируя данное уравнение, получим:

,

откуда и вытекает наше утверждение.

Решения однородного линейного уравнения обладают следующими двумя характерными для этого уравнения свойствами.

1. Если y₁ есть частное решение уравнения (4.3.3), т. е. имеет место тождество

(a<x<b), (4.3.16)

то функция

y=Cy₁, (4.3.17)

где C – произвольная постоянная, тоже является решением этого уравнения.

Действительно, полагая в левой части уравнения (4.3.3) y = Cy₁ и принимая во внимание тождество (4.3.16), получим:

(a<x<b).

Следовательно, y = Cy_l есть решение уравнения (4.3.3).

2. Если y₁ – ненулевое частное решение уравнения (4.3.3), то формула (4.3.17), где C – произвольная постоянная, дает общее решение уравнения (4.3.3) в области (4.3.7).

В самом деле, уравнение (4.3.17) разрешимо в области (4.3.7) относительно C:

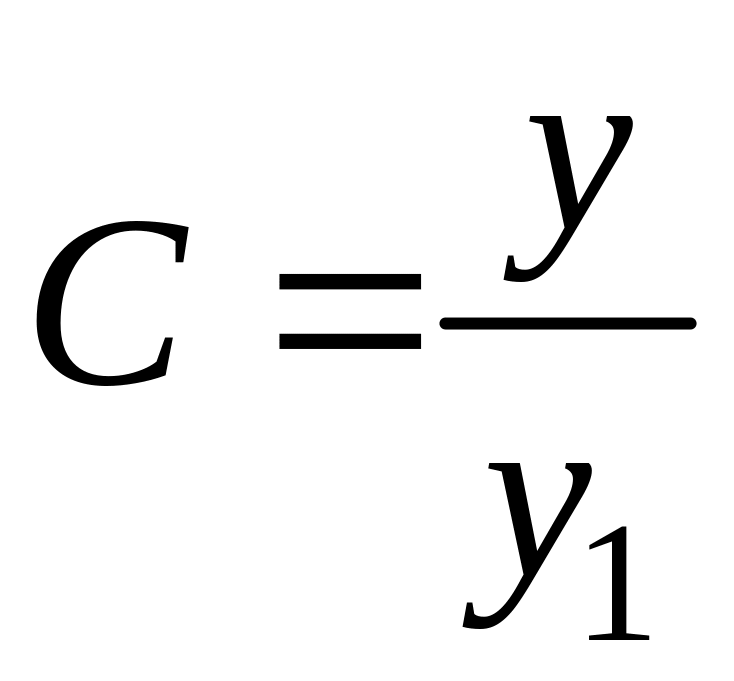(4.3.18)

и, как показано выше, функция (4.3.17) является решением уравнения (4.3.3) при всех значениях C. Следовательно, функция (4.3.17) есть общее решение уравнения (4.3.3) в области (4.3.7).

Таким образом, для построения общего решения однородного линейного уравнения достаточно найти какое-нибудь одно ненулевое частное решение.

Рассмотрим теперь неоднородное уравнение (4.3.1)

.

Предположим, что нам известно некоторое решение y₁ этого уравнения, т. е. имеем тождество:

(a<x<b), (4.3.19)

Введем новую неизвестную функцию z по формуле

y = y₁ + z (4.3.20)

Подставляя (4.3.20) в (4.3.1) имеем:

(4.3.21)

Отсюда, в силу тождества (4.3.19), получаем:

(4.3.22)

Мы получили для определения z однородное линейное уравнение, левая часть которого имеет тот же вид, что и левая часть уравнения (4.3.3).

Уравнение (4.3.22) называется однородным линейным уравнением, соответствующим неоднородному линейному уравнению (4.3.1). Общее решение уравнения (4.3.22) имеет вид:

(4.3.23)

где C – произвольная постоянная. Подставляя найденное значение z в (4.3.20), получим:

(4.3.24)

Все решения уравнения (4.3.1) содержатся в формуле (4.3.24). Эта формула представляет собою общее решение уравнения (4.3.1) в полосе

a< x <b, <y< + (4.3.25)

т. е. во всей области задания уравнения (4.3.1).

Таким образом, мы приходим к следующей теореме, устанавливающей структуру общего решения линейного неоднородного уравнения.

Теорема. Если y₁ есть частное решение неоднородного линейного уравнения (4.3.1),

то общее решение этого уравнения дается формулой (4.3.20),

y=y₁+z,

где

есть общее решение соответствующего однородного линейного уравнения (4.3.22),

.

Из этой теоремы следует, что знание одного частного решения неоднородного уравнения (4.3.1) дает возможность получить общее решение при помощи одной квадратуры.

Если мы знаем не одно, а два частных решения y₁ и y₂ неоднородного уравнения (4.3.1), то общее решение можно получить вовсе без квадратур, а именно общим решением будет

y=y₁+C(y₂y₁). (4.3.26)

Действительно, из формулы (4.3.20) имеем: z = y  y₁; заменяя здесь y на y₂, видим, что y₂y₁ есть частное решение однородного уравнения (4.3.22). Тогда общее решение уравнения (4.3.22) дается формулой z = С(y₂y₁) и, согласно доказанной теореме, формула (4.3.26) дает общее решение уравнения (4.3.1).

Выяснив структуру общего решения уравнения (4.3.1), укажем один общий способ фактического построения общего решения