5. Операция сложения векторов и ее свойства.

Определение 11. Суммой двух векторов a и b, называются такой третий вектор с, обозначаемый символом a + b, который изображается направленным отрезом , построенным следующим образом: из любой точки O откладывается направленный отрезок = a, из точки А откладывается направленный отрезок = b.

П

О

равило сложения векторов проиллюстрировано на рис. 8 и называется правилом треугольника.

Т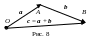 еорема 5. Сумма a + b любых двух векторов a и b определяется однозначно.

Д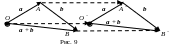 оказательство. В силу теоремы 4 достаточно доказать, что сумма векторов не зависит от выбора начальной точки О. Построим две суммы a + b векторов a и b, выбирая в качестве начальных точек две различные точки О и О (см. рис 9). Покажем, что . Так как и , то по следствию 2 теоремы 3 и . Тогда по теореме 2 . Отсюда, применяя следствие 2 теоремы 3 получаем .

Теорема 6. Для любых векторов a, b, c справедливы свойства:

1) a + b = b + a - коммутативный закон сложения;

2) a + (b + c) = (a + b) + c - ассоциативный закон сложения;

3) a + 0 = a - свойство нулевого вектора;

4) a + (-a) = 0 - свойство противоположно

Доказательство. Справедливость свойств 1 и 2 вытекает из определения 11 (см. рис. 10 и 11), а свойств 3 и 4 из определений нулевого и противоположного векторов. 

С умму двух неколлинеарных векторов a и b можно найти по правилу параллелограмма . Для этого необходимо из одной точки O отложить оба вектора a = и b = и построить параллелограмм OADB на векторах и (см. рис. 10). Тогда суммой a + b векторов a и b изображается направленным отрезком диагонали параллелограмма.

Сумму любого конечного числа векторов можно найти по правилу многоугольника (см. рис. 12).

5. Вычитание векторов.

Определение 12. Разностью двух векторов a и b, называются такой третий вектор с, обозначаемый символом a - b, при сложении которого с вектором b получаем вектор a.

Теорема 7. Для любых векторов a, b разность a - b существует, единственна и вычисляется по формуле:

a - b = a + (-b). (1)

Доказательство. Так как

(a + (-b)) + b = a + ((-b) + b) = a + 0 = a,

то вектор a + (-b) разность векторов a и b. Доказывая единственность разности допустим, что векторы с и d являются разностью векторов a и b. Тогда по определению разности имеем b + с = a и b +d = a. Отсюда b + с = b +d. Прибавляя к обеим частям этот равенства вектор получаем (-b) + (b + с) = (-b)+ (b +d). Применяя свойства теоремы 6 последовательно получаем равенства:

((-b) + b) + с) = ( (-b)+ b) +d,

0 + с = 0 +d,

с = d.

Разность векторов a и b геометрически можно найти двумя способами по определению 12 (см. рис. 13) и по теореме 7 (см. рис 14). По определению 12 разность a - b равна вектору, выходящему из конца второго вектора b в начало первого a, если векторы a и b отложены от одной точки. По теореме 7 разность a - b равна сумме векторов a + (-b).

7. Операция умножения вектора на число и ее свойства.

Определение 13. Произведением вектора a на число  называется такой вектор b, что

1)  b  =    a 

2) если  > 0, то ab, если  < 0, то ab, если  = 0 или a = 0, то b = 0.

Произведение вектора a на число  обозначается символом  a. Числа называют также скалярными величинами или скалярами.

Теорема 8. Вектора a  0 коллинеарен вектору b тогда и только тогда, когда найдется такое число, что b =  a.

Доказательство. Если , то по определения 13 следует, что векторы коллинеарны. Обратно, пусть вектора коллинеарны. Тогда, полагая  = b/a, где стоит знак "+", если ab, стоит знак "-", если ab, по определению 13 получим b =  a.

Теорема 9. Для любых векторов a, b и для любых чисел ,  справедливы свойства:

1) ( a) = () a - смешенный ассоциативный закон;

2) ( + ) a =  a+  a - дистрибутивный закон;

3)  (a + b) =  a +  b - дистрибутивный закон;

4) 1 a = a - свойство умножения на единицу.

Доказательство. 1. Если векторы a или b равны 0 или числа  равны нулю, то равенства 1-3 теоремы почти очевидны (проверте их). Также по определению равенства векторов проверяется равенство 4. Поэтому дальше будем считать, что a  0, b  0,   0.

1. Длины векторов ( a), () a равны  a, и поэтому равны между собой. Далее оба эти вектора коллинеарны вектору a. Если числа  и  одного знака, то направление векторов ( a), () a совпадает с направлением вектора a. Если числа  и  противоположных знаков, то эти векторы противоположны вектору a. Отсюда по определению векторы ( a), () a равны.

2. Если числа  и  одного знака, то векторы ( + ) a,  a,  a сонаправлены и  a+ a =  a+ a=  a +   a = (   +    ) a.

Так как в этом случае  +   =    +   , то ( + ) a =   a +  a.

Отсюда, по определению равенства векторов ( + ) a =  a +  a.

Случай, когда числа  и  противоположного знака рассмотрите самостоятельно.

3. Если векторы a и b коллинеарны, то по теореме 8 его можно представить в виде b =  a. Тогда по свойствам 1, 2 и 4 имеем

 (a + b) =  (1a +  a) =  (1a) +  ( a) = a +  ( a) =  a +  b.

Е сли векторы a и b неколлинеарны, то построим сумму a + b = = + . Построим вектор  a = ,  (a + b) = (см. рис. 15 при  > 0 и рис. 16 при  < 0). Получим, что треугольники ОAB и OCD подобны. Из подобия треугольников и определения 13 получаем, что =  a. Отсюда находим, что  (a + b) = = = + =a +  b.

Пространство геометрических векторов. Множество V₃ всех геометрических векторов пространства является векторным пространством на полем действительных чисел относительно операций сложения векторов и умножения вектора на число (см. теоремы 6 и 9 § 1).. Также векторным пространством является множество V₂ (V₁) всех векторов плоскости (прямой).

Множество всех геометрических векторов, коллинеарных данному вектору a образует подпространство пространства V₃ всех геометрических векторов.