
- •§ 1. Функции нескольких переменных
- •§ 2. Понятие предела функции двух и более переменных
- •§ 3. Непрерывность функций нескольких переменных
- •§4. Частные производные
- •§5. Дифференцируемость функции нескольких переменных
- •§ 6 Необходимые условия дифференцируемости
- •§7 Достаточные условия дифференцируемости.
- •§8 Дифференциал
- •§9 Касательная плоскость и нормаль к поверхности.
- •§10 Производные сложных функций.
- •§11 Экстремум функции
- •§12 Отыскание наибольших и наименьших значений функции двух независимых переменных в замкнутой области.
- •§14. Метод множителей Лагранжа.
- •§16. Касательная плоскость и нормаль к поверхности.
- •22Вопрос
- •27Вопрос
- •29 Вопрос
- •Формулы прямоугольников.
- •Формула трапеций.
- •Формула Симпсона.
- •30. Вопрос
- •31 Вопрос
- •40 Вопрос Вычисление
31 Вопрос
Пусть
ограниченная
замкнутая область плоскости
![]() с
кусочно-гладкой границей и пусть функция
определена
и ограничена на
.
Посредством сетки кусочно-гладких
кривых разобьем
на
конечное число элементарных областей
с
кусочно-гладкой границей и пусть функция
определена
и ограничена на
.
Посредством сетки кусочно-гладких
кривых разобьем
на
конечное число элементарных областей
![]() с
площадями
с
площадями
![]() (разбиение
(разбиение
![]() ).
Пусть
).
Пусть
![]() -
наибольший из диаметров областей
-
наибольший из диаметров областей
![]() ,
получающийся при разбиении
.
В каждой из элементарных областей
выберем произвольную точку
,
получающийся при разбиении
.
В каждой из элементарных областей
выберем произвольную точку
![]() .
Число
.
Число
![]() называется
интегральной суммой и ставится в
соответствие каждому разбиению
и
каждому выбору точек
называется
интегральной суммой и ставится в
соответствие каждому разбиению
и
каждому выбору точек
![]() .
Если существует
.
Если существует
![]() и
он не зависит от выбора разбиения
и
точек
,
то функция называется интегрируемой
по Риману в области
,
а сам предел называется двойным интегралом
от функции
по
области
и
обозначается
и
он не зависит от выбора разбиения
и
точек
,
то функция называется интегрируемой
по Риману в области
,
а сам предел называется двойным интегралом
от функции
по
области
и
обозначается
![]() или
или
![]() .
Двойной интеграл существует, если
непрерывна
на
.
Допустимы точки разрыва первого рода,
лежащие на конечном числе гладких кривых
в
.
.
Двойной интеграл существует, если
непрерывна
на
.
Допустимы точки разрыва первого рода,
лежащие на конечном числе гладких кривых
в
.
32. вопрос
Двойной интеграл в полярных координатах.
Вычисление
![]() Пусть
требуется посчитать
Пусть
требуется посчитать
![]() по
области
по
области
![]() ,
которая задается в полярных координатах
условиями
,
которая задается в полярных координатах
условиями
![]() .
.
Сделаем
замену переменных
![]() .При
этой замене нарушается взаимная
однозначность отображения. Точке
.При
этой замене нарушается взаимная
однозначность отображения. Точке
![]() соответствует
целый отрезок
соответствует
целый отрезок
![]() на
оси
на
оси
![]() .
Однако точка имеет нулевую площадь и
теорема справедлива. Осталось вычислить
.
Однако точка имеет нулевую площадь и
теорема справедлива. Осталось вычислить
![]() .
.
![]() ,
,
![]() .
.
![]() .Следовательно,
.Следовательно,
![]() .
.
33. вопрос
Тройной интеграл.
При рассмотрении тройного инеграла не будем подробно останавливаться на всех тех теоретических выкладках, которые были детально разобраны применительно к двойному интегралу, т.к. существенных различий между ними нет.
Единственное отличие заключается в том, что при нахождении тройного интеграла интегрирование ведется не по двум, а по трем переменным, а областью интегрирования является не часть плоскости, а некоторая область в техмерном пространстве.
![]()
Суммирование производится по области v, которая ограничена некоторой поверхностью (x, y, z) = 0.
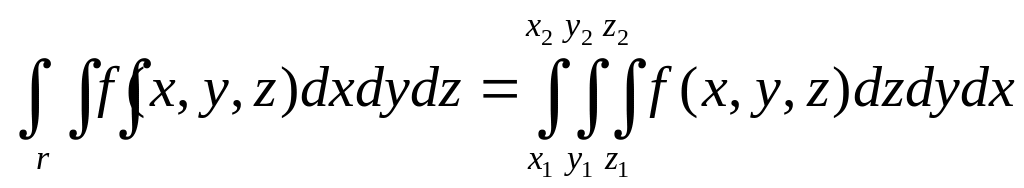
Здесь х1 и х2 – постоянные величины, у1 и у2 – могут быть некоторыми функциями от х или постоянными величинами, z1 и z2 – могут быть функциями от х и у или постоянными величинами.
Тройной интеграл. Его основные свойства и приложения. Вычисление тройного интеграла
Рассмотрим
кубируемую область в трехмерном
пространстве
![]() .
Разбиение
.
Разбиение
![]() на
части
на
части
![]() осуществляется
непрерывными поверхностями. Диаметр
разбиения определяется аналогично
двумерному случаю. Также, по аналогии,
можно определить для функции
осуществляется
непрерывными поверхностями. Диаметр
разбиения определяется аналогично
двумерному случаю. Также, по аналогии,
можно определить для функции
![]() ,
разбиения
области
,
разбиения
области
![]() и
выбранных точек
и
выбранных точек
![]() интегральную
сумму
интегральную
сумму
![]() ,
где
,
где
![]() обозначает
объем области
.
обозначает
объем области
.
Определение.
Пусть
![]() такое
число, что
такое
число, что
![]()
![]() .
Тогда мы говорим, что
.
Тогда мы говорим, что
![]() интегрируема
на
,
число
интегрируема
на
,
число
![]() есть
интеграл
по
области
и
обозначаем это так:
есть
интеграл
по
области
и
обозначаем это так:
![]() .Как
и в случае двойного интеграла, выполняются
аналогичные свойства 1-6. Можно доказать,
что если
непрерывна
на
,
то она интегрируема на
.
Точно также можно убедиться в том, что
если точки разрыва
лежат
на конечном числе непрерывных поверхностей,
лежащих в
и
разбивающих
на
кубируемые области, то
интегрируема
на
.
.Как
и в случае двойного интеграла, выполняются
аналогичные свойства 1-6. Можно доказать,
что если
непрерывна
на
,
то она интегрируема на
.
Точно также можно убедиться в том, что
если точки разрыва
лежат
на конечном числе непрерывных поверхностей,
лежащих в
и
разбивающих
на
кубируемые области, то
интегрируема
на
.
Вычисление тройного интеграла производится по следующему правилу.
Теорема.
Пусть
задана
следующими неравенствами:
![]() ,
,
![]() .
-
квадрируемая область на плоскости,
.
-
квадрируемая область на плоскости,
![]() -
непрерывные. Тогда
-
непрерывные. Тогда
![]()
Замечание.
Если область
задана
неравенствами
![]() ,
где
,
где
![]() -
непрерывные функции, то
-
непрерывные функции, то
![]()
34. вопрос
Цилиндрическая система координат.
Связь координат произвольной точки Р пространства в цилиндрической системе с координатами в декартовой прямоугольной системе осуществляется по формулам:
![]()
![]()
Для представления тройного интеграла в цилиндрических координатах вычисляем Якобиан:
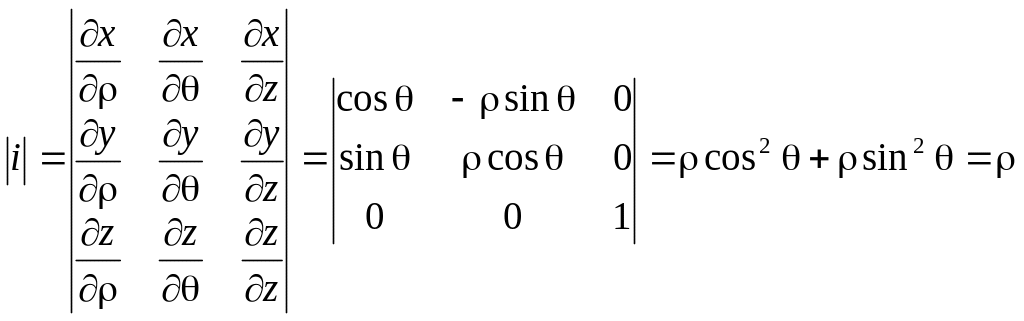
Итого:
![]()
Сферическая система координат.
Связь координат произвольной точки Р пространства в сферической системе с координатами в декартовой прямоугольной системе осуществляется по формулам:
![]()
![]()
Для представления тройного интеграла в сферических координатах вычисляем Якобиан:
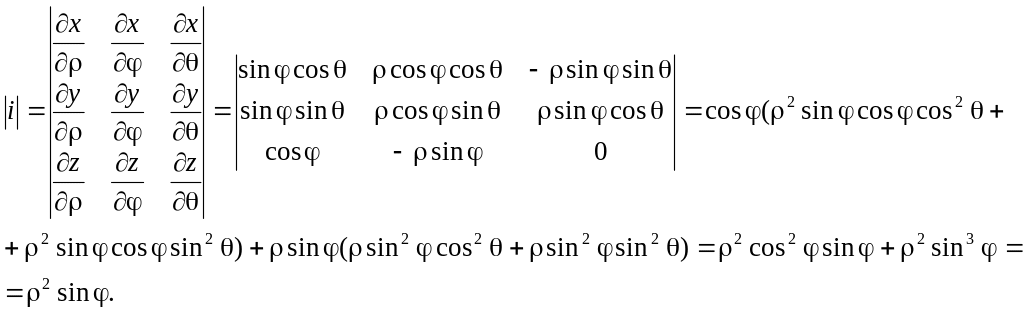
Окончательно получаем:
![]()
38 вопрос
Корни многочлена
Как мы
видели выше, методом выделения полного
квадрата можно найти корни квадратного
трехчлена. В случае многочленов высших
степеней найти корни становится гораздо
труднее, а иногда и просто невозможно.
Попробуем это сделать там, где это
достаточно просто. Рассмотрим многочлен
![]() где
a 1,
a 2, ...,
a n
−
целые числа, a n
≠ 0.
Теорема
о рациональных корнях многочлена
Если многочлен
где
a 1,
a 2, ...,
a n
−
целые числа, a n
≠ 0.
Теорема
о рациональных корнях многочлена
Если многочлен
![]() с
целыми коэффициентами имеет рациональный
корень
с
целыми коэффициентами имеет рациональный
корень
![]() то
число p является делителем числа
то
число p является делителем числа
![]() (свободного
члена), а число q является делителем
числа
(свободного
члена), а число q является делителем
числа
![]() (старшего
коэффициента).
(старшего
коэффициента).
Доказательство
Действительно,
если число
![]() является
корнем многочлена
является
корнем многочлена
![]() то
то
![]() а
именно:
а
именно:
![]() Умножим
обе части этого уравнения на
Умножим
обе части этого уравнения на
![]() получим:
получим:
![]() Так
как
Так
как
![]() −
целые числа, то в скобке стоит целое
число. Значит, вся правая часть этого
равенства делится на q , так как q входит
в неё в качестве сомножителя. А значит
и левая часть тождества делится на q ,
так как она равна правой. Число p не
делится на q , так как иначе дробь
−
целые числа, то в скобке стоит целое
число. Значит, вся правая часть этого
равенства делится на q , так как q входит
в неё в качестве сомножителя. А значит
и левая часть тождества делится на q ,
так как она равна правой. Число p не
делится на q , так как иначе дробь
![]() была
бы сократимой, значит и
была
бы сократимой, значит и
![]() не
делится на q . Следовательно, на q делится
единственный из оставшихся сомножителей
левой части, а именно
не
делится на q . Следовательно, на q делится
единственный из оставшихся сомножителей
левой части, а именно
![]() Аналогично
доказывается, что
делится
на p . Теорема доказана.
Аналогично
доказывается, что
делится
на p . Теорема доказана.
39 вопрос
свойства:
1) Криволинейный
интеграл при перемене направления
кривой меняет знак.
![]()
2) ![]()
3)
![]()
4)
![]()
5) Криволинейный интеграл по замкнутой кривой L не зависит от выбора начальной точки, а зависит только от направления обхода кривой.
![]()
Криволинейный интеграл 2-го рода
Рассмотрим кривую AB, которую пока считаем незамкнутой.
Пусть
проекция этой кривой на ось x
представляет собой отрезок
![]() .
.
Пусть
точки
![]() дают
разбиение кривой AB.
Рассмотрим их проекции
дают
разбиение кривой AB.
Рассмотрим их проекции
![]() ,
лежащие на отрезке
и
обозначим
,
лежащие на отрезке
и
обозначим
![]() .
.
(Отметим,
что точки
не
обязательно упорядочены так:
![]() ,
т.е. не обязательно дают разбиение
отрезка
,
поэтому некоторые
,
т.е. не обязательно дают разбиение
отрезка
,
поэтому некоторые
![]() могут
быть меньше 0!).
могут
быть меньше 0!).
Пусть
![]() -
определена на AB.
Пусть
-
определена на AB.
Пусть
![]() -
точка, лежащая на кривой между
-
точка, лежащая на кривой между
![]() и
и
![]() .
Положим
.
Положим
![]() .
.
Определение.
Пусть
![]() .
Если
.
Если
![]() ,
то говорят, что I
- это криволинейный
интеграл второго типа
,
то говорят, что I
- это криволинейный
интеграл второго типа
![]()
