27Вопрос

Вычисление длины дуги

Длина ломаной линии, которая соответствует дуге, может быть найдена как .

Тогда длина дуги равна .

Из геометрических соображений:

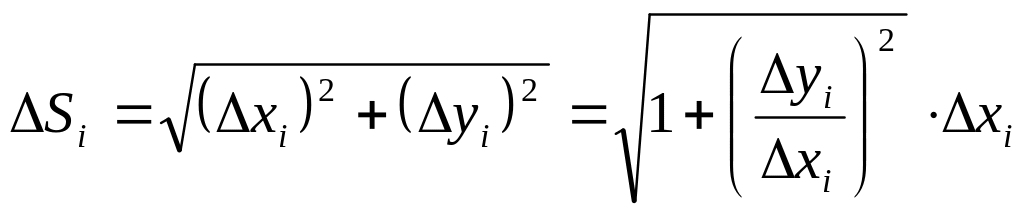
Если дуга задана в полярной системе координат, то

. Поэтому .

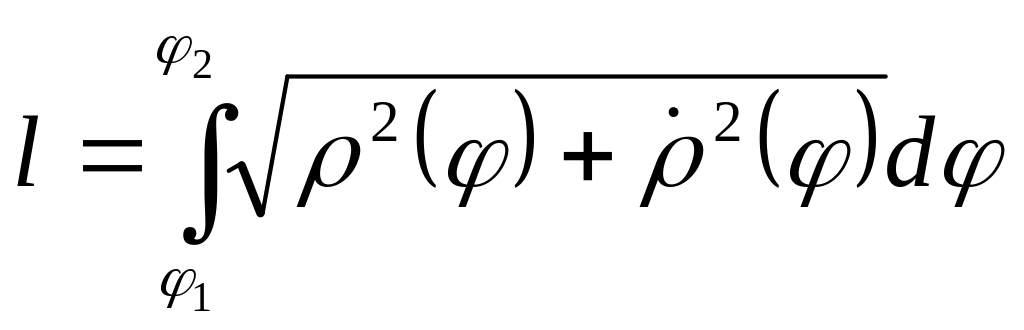Площадь поверхности тела вращения.

Определение: Площадью поверхности вращения кривой АВ вокруг данной оси называют предел, к которому стремятся площади поверхностей вращения ломаных, вписанных в кривую АВ, при стремлении к нулю наибольших из длин звеньев этих ломаных.

Разобьем дугу АВ на n частей точками M₀, M₁, M₂, … , M_n. Координаты вершин полученной ломаной имеют координаты x_i и y_i. При вращении ломаной вокруг оси получим поверхность, состоящую из боковых поверхностей усеченных конусов, площадь которых равна P_i. Эта площадь может быть найдена по формуле:

Здесь S_i – длина каждой хорды.

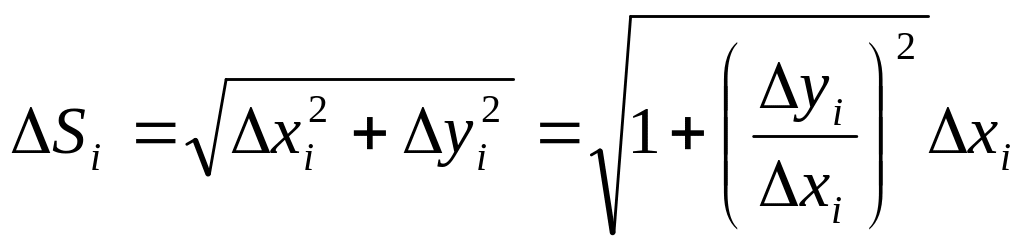
Применяем теорему Лагранжа (см. Теорема Лагранжа.) к отношению .

Получаем:

Тогда

Площадь поверхности, описанной ломаной равна:

Эта сумма не является интегральной, но можно показать, что

Тогда - формула вычисления площади поверхности тела вращения.

28 вопрос

Пусть функция f(x) определена и непрерывна на интервале [a, ). Тогда она непрерывна на любом отрезке [a, b].

Определение: Если существует конечный предел , то этот предел называется несобственным интегралом от функции f(x) на интервале [a, ).

Обозначение:

Если этот предел существует и конечен, то говорят, что несобственный интеграл сходится.

Если предел не существует или бесконечен, то несобственный интеграл расходится.

Аналогичные рассуждения можно привести для несобственных интегралов вида:

Конечно, эти утверждения справедливы, если входящие в них интегралы существуют.

Несобственные интегралы (второго рода).

Функция может терпеть разрыв на левом конце отрезка , на правом конце или в некоторой внутренней точке с отрезка.

Пусть функция непрерывна на отрезке за исключением точки x= a, тогда несобственным интегралом второго рода от функции по отрезку называется предел

=

.Пусть функция непрерывна на отрезке за исключением точки x= b, тогда несобственным интегралом второго рода от функции по отрезку называется предел = .

29 Вопрос

1. Формулы прямоугольников.

Обозначим . Заменим интеграл интегральной суммой, вычисляя площадь под графиком функции как сумму площадей прямоугольников с основанием h, высотами .

Если на первом отрезке высоту прямоугольника можно выбрать как , тогда на последнем отрезке высота прямоугольника . Получим первую формулу прямоугольников

.

Если на первом отрезке высоту прямоугольника можно выбрать как , тогда на последнем отрезке высота прямоугольника . Получим вторую формулу прямоугольников

.

Оценим погрешность формул прямоугольников. Разложим в ряд Тейлора и оценим остаточный член.

Для первой формулы прямоугольников

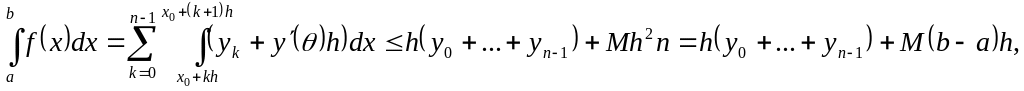где .

Для второй формулы прямоугольников

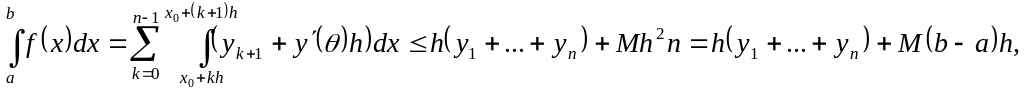где .

Таким образом, обе формулы прямоугольников дают погрешность порядка h и являются формулами первого порядка точности.

Можно повысить точность формулы прямоугольников за счет вычисления функции в серединах отрезков разбиения. Получаем третью формулу прямоугольников

.

Оценим погрешность этой формулы.

+

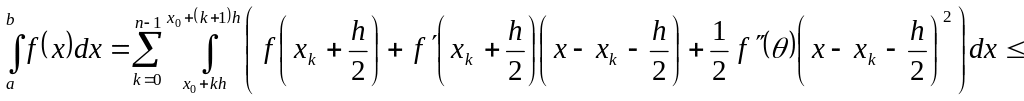
+0+

Таким образом, погрешность третьей формулы прямоугольников не превышает , где . Эта формула прямоугольников имеет второй порядок точности.