
- •Методы конечномерной оптимизации
- •390005, Рязань, ул. Гагарина, 59/1.
- •Лабораторная работа № 1 Методы одномерной оптимизации
- •1. Краткие теоретические сведения
- •1.1. Метод золотого сечения
- •1.3. Методы с использованием производных
- •2. Исходные данные
- •3. Порядок выполнения работы
- •4. Содержание отчета
- •Лабораторная работа № 2 Методы безусловной оптимизации функций многих переменных
- •3. Порядок выполнения работы
- •4. Содержание отчета
- •Лабораторная работа № 3 Линейное программирование
- •1. Краткие теоретические сведения
- •Теорема о существовании решений. Задача линейного программирования вида (3.1) или (3.3) имеет решение тогда и только тогда, когда допустимые множества прямой и двойственной задачи не пусты, т.Е.
- •2. Содержание работы
- •3. Порядок выполнения работы
- •4. Содержание отчета
- •Лабораторная работа № 4 Дискретное программирование
- •2. Порядок выполнения работы
- •3. Содержание отчета
1.3. Методы с использованием производных
Рассмотренные методы поиска используют информацию только о значениях целевой функции. Логично предположить, что если дополнительно к этому иметь информацию о производных функции, то эффективность поисковых процедур может существенно повыситься.
Метод средней
точки. Если
функция
![]() унимодальная
в заданном интервале поиска
унимодальная
в заданном интервале поиска
![]() ,
то точкой оптимума является точка, в
которой
,
то точкой оптимума является точка, в
которой
![]()
![]() .
Если при этом имеется возможность
вычислять как значения функции, так и
ее производные, то для нахождения корня
уравнения
.
Если при этом имеется возможность
вычислять как значения функции, так и
ее производные, то для нахождения корня
уравнения
![]() можно воспользоваться эффективным
алгоритмом исключения интервалов, на
каждой итерации которого рассматривается
лишь одна пробная точка.
можно воспользоваться эффективным
алгоритмом исключения интервалов, на
каждой итерации которого рассматривается
лишь одна пробная точка.
Вычислим значение
производной функции в средней точке
рассматриваемого интервала
![]() .
Если
.
Если
![]() ,
то с учетом предположения об унимодальности
естественно утверждать, что точка
минимума не может находиться левее
точки
,
то с учетом предположения об унимодальности
естественно утверждать, что точка
минимума не может находиться левее
точки
![]() .
Другими словами, интервал
.
Другими словами, интервал
![]() подлежит исключению. С другой стороны,
если
подлежит исключению. С другой стороны,
если
![]() ,
то точка минимума не может находиться
правее z
и интервал
,
то точка минимума не может находиться
правее z
и интервал
![]() можно исключить [1]. Приведенные
рассуждения лежат в основе логической
структуры метода средней точки,
называемого иногда поиском Больцано,
который включает следующие шаги.
можно исключить [1]. Приведенные
рассуждения лежат в основе логической
структуры метода средней точки,
называемого иногда поиском Больцано,
который включает следующие шаги.
Шаг 1.
Задать интервал поиска
и величину
![]() ,
определяющую точность нахождения точки
минимума
,
определяющую точность нахождения точки
минимума
![]() ;
при этом
;
при этом
![]() и
и
![]() .
.
Шаг 2.
Вычислить
и
![]() .
.
Шаг 3. Если
![]() |,
закончить поиск, положив
|,
закончить поиск, положив
![]() .
.
В противном случае,
если
,
положить
![]() и перейти к шагу 2; если
,
положить
и перейти к шагу 2; если
,
положить
![]() и перейти к шагу 2.
и перейти к шагу 2.
Следует отметить, что логическая структура поиска в соответствии с изложенным методом исключения интервалов основана лишь на исследовании знака производной независимо от значений, которые эта производная принимает.
Метод
секущих. Метод
секущих, являющийся комбинацией метода
Ньютона и общей схемы исключения
интервалов, ориентирован на нахождение
корня уравнения
![]() в интервале
(a,
b),
если, разумеется, такой корень существует.
в интервале
(a,
b),
если, разумеется, такой корень существует.
Предположим, что
в процессе поиска стационарной точки
функции
в интервале (a,
b)
обнаружены две точки
![]() и
и
![]() ,
в которых знаки производной различны.
В этом случае алгоритм метода секущих
позволяет аппроксимировать функцию
«секущей
прямой» (прямой линией, соединяющей
две точки) и найти точку, в которой
секущая графика
пересекает
ось абсцисс (см. рисунок). Таким образом,
следующее приближение к стационарной
точке
,
в которых знаки производной различны.
В этом случае алгоритм метода секущих
позволяет аппроксимировать функцию
«секущей
прямой» (прямой линией, соединяющей
две точки) и найти точку, в которой
секущая графика
пересекает
ось абсцисс (см. рисунок). Таким образом,
следующее приближение к стационарной
точке
![]() определяется по формуле
определяется по формуле
![]() .
(1.4)
.
(1.4)
Если
![]() ,
поиск следует закончить. В противном
случае необходимо выбрать одну из точек
или
таким
образом, чтобы знаки производной в этой
точке и точке z
были различны, а затем повторить основной
шаг алгоритма [2].
,
поиск следует закончить. В противном
случае необходимо выбрать одну из точек
или
таким
образом, чтобы знаки производной в этой
точке и точке z
были различны, а затем повторить основной
шаг алгоритма [2].
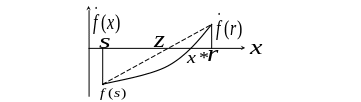
Алгоритм для данного метода приводится ниже.
Шаг 1.
Задать интервал поиска
и величину
,
определяющую точность нахождения точки
минимума
;
положить
![]() ;
при этом
;
при этом
![]() и
и
![]() .
.
Шаг 2.
Вычислить текущее приближение z
к минимуму
по формуле (1.4). Вычислить
![]() .
.
Шаг 3.
Если
,
закончить поиск. В противном случае,
если
![]() ,
положить
,
положить
![]() и перейти
к шагу 2.
Если
и перейти
к шагу 2.
Если
![]() ,
положить
,
положить
![]() и перейти
к шагу 2.
и перейти
к шагу 2.
