
- •Методы конечномерной оптимизации
- •390005, Рязань, ул. Гагарина, 59/1.
- •Лабораторная работа № 1 Методы одномерной оптимизации
- •1. Краткие теоретические сведения
- •1.1. Метод золотого сечения
- •1.3. Методы с использованием производных
- •2. Исходные данные
- •3. Порядок выполнения работы
- •4. Содержание отчета
- •Лабораторная работа № 2 Методы безусловной оптимизации функций многих переменных
- •3. Порядок выполнения работы
- •4. Содержание отчета
- •Лабораторная работа № 3 Линейное программирование
- •1. Краткие теоретические сведения
- •Теорема о существовании решений. Задача линейного программирования вида (3.1) или (3.3) имеет решение тогда и только тогда, когда допустимые множества прямой и двойственной задачи не пусты, т.Е.
- •2. Содержание работы
- •3. Порядок выполнения работы
- •4. Содержание отчета
- •Лабораторная работа № 4 Дискретное программирование
- •2. Порядок выполнения работы
- •3. Содержание отчета
4009
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
РЯЗАНСКИЙ ГОСУДАРСТВЕННЫЙ РАДИОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Методы конечномерной оптимизации
Методические указания
к лабораторным работам
Рязань 2007
УДК 519.6
Методы конечномерной оптимизации: методические указания к лабораторным работам / Рязан. гос. радиотехн. ун-т; сост. Ю.А. Филатов.- Рязань, 2007. - 24 с.
Содержат описания четырех лабораторных работ по курсу «Методы конечномерной оптимизации».
Предназначены студентам дневного отделения специальности 080116 «Математические методы в экономике».
В постановке лабораторных работ принимали участие студенты группы 332: Комарова М.О., Самуленок Л.Л., Куликов А.А., Фомин Н.В.
Табл. 4. Ил. 4. Библиогр.: 7 назв.
Отрезок локализации, точка минимума функции, алгоритм поиска, безусловная оптимизация, условная оптимизация, пакет оптимизации системы Matlab, прямая задача линейного программирования, двойственная задача линейного программирования
Печатается по решению редакционно-издательского совета Рязанского государственного радиотехнического университета.
Рецензент: кафедра эконометрики и математического моделирования РГРТУ (зав. кафедрой проф. Е.П. Чураков)
Методы конечномерной оптимизации
Составитель Ф и л а т о в Юрий Анатольевич
Редактор Н.А. Орлова
Корректор С.В. Макушина
Подписано в печать 20.12.07 . Формат бумаги 60х84 1/16.
Бумага газетная. Печать трафаретная. Усл. печ. л. 1,5.
Уч.-изд. л. 1,5. Тираж 50 экз. Заказ
Рязанский государственный радиотехнический университет.
390005, Рязань, ул. Гагарина, 59/1.
Редакционно–издательский центр РГРТУ.
Лабораторная работа № 1 Методы одномерной оптимизации
Цель работы: ознакомление с методами одномерной минимизации унимодальных функций в среде Mathcad.
1. Краткие теоретические сведения
Задача
минимизации функции одной переменной
(задача одномерной минимизации) относится
к наиболее простому типу оптимизационных
задач. Подобные задачи достаточно часто
встречаются в экономике, а алгоритмы
одномерной оптимизации используются
во многих вычислительных процедурах
поиска экстремума функций многих
переменных. В работе рассматриваются
методы в предположении, что исследуемая
функция
![]() ,
называемая целевой,
является унимодальной [1,2].
,
называемая целевой,
является унимодальной [1,2].
Задача
одномерной минимизации ставится
следующим образом. Требуется найти
точку минимума унимодальной на отрезке
![]() целевой функции с абсолютной ошибкой
целевой функции с абсолютной ошибкой
![]() .
Формально эта задача записывается так:
.
Формально эта задача записывается так:
![]() .
(1.1)
.
(1.1)
Рассмотрим кратко некоторые часто используемые методы одномерной минимизации [1,2].
1.1. Метод золотого сечения
Данный метод
основан на свойствах точек золотого
сечения
![]() отрезка
отрезка
![]() [1]:
[1]:
точки размещаются на одинаковых расстояниях от середины отрезка;
точка
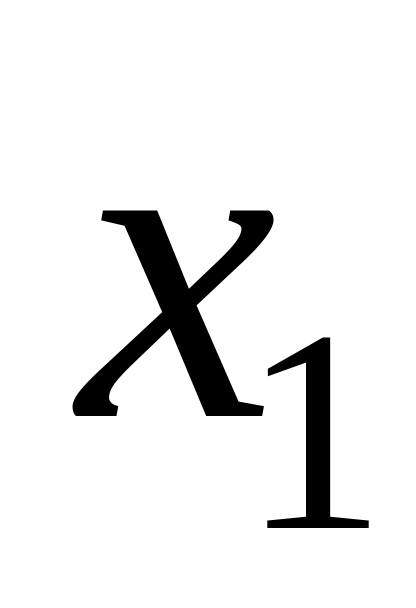 является второй точкой золотого сечения
отрезка
является второй точкой золотого сечения
отрезка
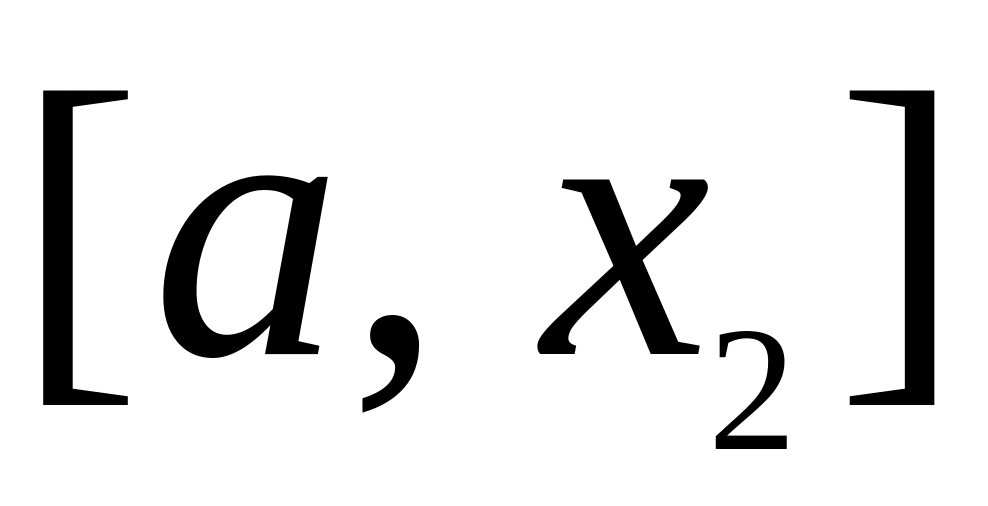 ,
а точка
,
а точка
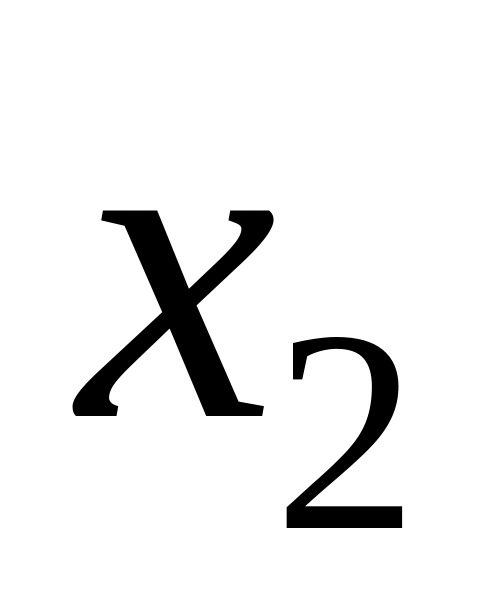 -
первой точкой золотого сечения отрезка
-
первой точкой золотого сечения отрезка
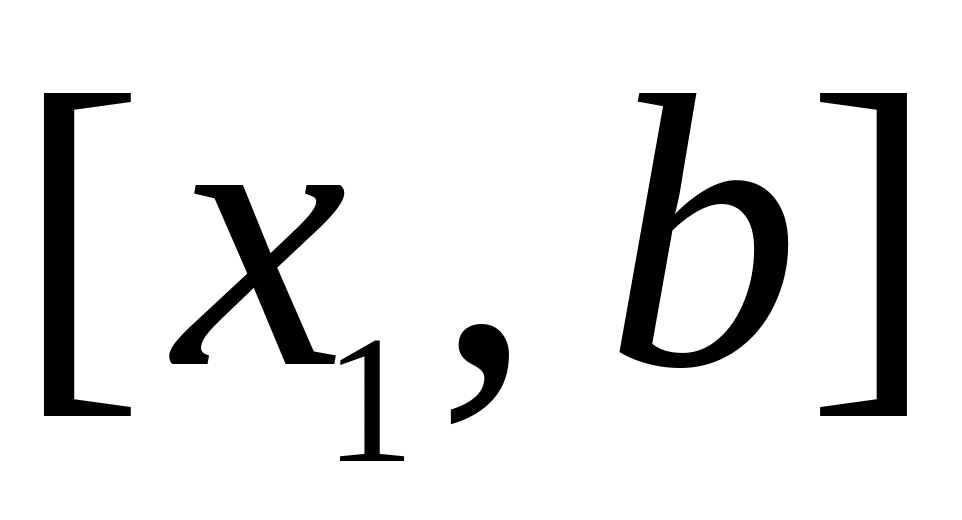 ;
;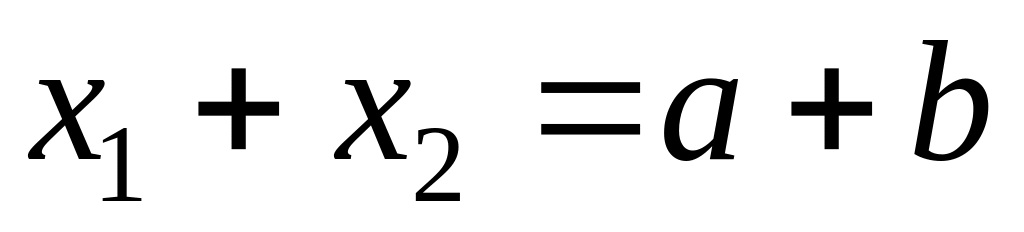 .
.
Алгоритм золотого сечения, удобный для реализации на ЭВМ, включает следующие шаги [1].
Шаг 1. Задаемся абсолютной ошибкой оценки точки минимума . Вычисляем точки отрезка , содержащего точку минимума [1]
![]() ,
(1.2)
,
(1.2)
где
![]() .
.
Определяем
значения функции в этих точках
![]() .
.
Шаг
2. Сравниваем
значения
![]() и
и
![]() .
.
Если
![]() ,
то исключается интервал
,
то исключается интервал
![]() ,
и отрезком локализации становится
отрезок
,
и отрезком локализации становится
отрезок
![]() .
.
Полагаем
![]() .
Вычисляем
(1.2) и
.
Вычисляем
(1.2) и
![]() .
Переходим к шагу 3.
.
Переходим к шагу 3.
Если
![]() ,
то исключается интервал
,
то исключается интервал
![]() ,
и дальнейший поиск точки минимума
осуществляется на отрезке
,
и дальнейший поиск точки минимума
осуществляется на отрезке
![]() .
.
Полагаем
![]() .
Вычисляем
.
Вычисляем
![]() (1.2) и
(1.2) и
![]() .
.
Шаг
3. Вычисляем
абсолютную ошибку, с которой определяется
искомая точка минимума на новом отрезке
локализации
![]() .
.
Если
![]() ,
то
,
то
![]() .
Поиск заканчивается.
.
Поиск заканчивается.
Если
![]() ,
то переходим к шагу 2.
,
то переходим к шагу 2.
Из описания алгоритма видно, что на каждой итерации, за исключением первой, выполняется одно вычисление значения целевой функции.
1.2. Метод Фибоначчи
Для
применения метода требуется указать
число N
вычислений целевой функции, обеспечивающее
заданную точность нахождения точки
минимума на отрезке
![]() длиной
длиной
![]() .
Для этого по заданной абсолютной ошибке
.
Для этого по заданной абсолютной ошибке
![]() определяется величина
определяется величина
![]() ,
округляемая до большего числа Фибоначчи
,
округляемая до большего числа Фибоначчи
![]() ,
а затем число необходимых шагов N.
,
а затем число необходимых шагов N.
Числа
Фибоначчи, определяются из условий
![]()
![]()
![]() .
.
Алгоритм Фибоначчи включает следующие шаги [2].
Шаг
1.
На первой итерации
![]() определяются две точки исходного
отрезка
определяются две точки исходного
отрезка
![]()
![]() (1.3)
(1.3)
расположенные
симметрично относительно середины
отрезка
,
в которых вычисляются значения функции
![]() и
и
![]() .
.
Шаг
2.
Полагаем
![]() .
Если
.
Если
![]() ,
то отрезком локализации точки минимума
функции становится отрезок
,
то отрезком локализации точки минимума
функции становится отрезок
![]() длиной
длиной
![]() ,
включающий точку
,
включающий точку
![]() .
.
Полагаем
![]() ,
вычисляем точку
,
вычисляем точку
![]()
значение функции в ней и переходим к шагу 3.
Если
,
то отрезком локализации точки минимума
функции становится отрезок
![]() той же длины, включающий точку
той же длины, включающий точку
![]() .
.
Полагаем
![]() ,
вычисляем точку
,
вычисляем точку
![]() ,
,
значение функции в ней .
Шаг
3.
Если
![]() ,
то осуществляется переход к шагу 2.
,
то осуществляется переход к шагу 2.
Если
![]() ,
то программа останавливается,
,
то программа останавливается,
![]() .
.
После
(N-1)-го
шага вычисляемые точки
![]() сливаются в одну и оказываются в середине
отрезка локализации длиной
сливаются в одну и оказываются в середине
отрезка локализации длиной
![]() .
Эта точка аппроксимирует локализованную
на этом отрезке точку минимума
.
Эта точка аппроксимирует локализованную
на этом отрезке точку минимума
![]() с ошибкой, не превышающей половины
данного отрезка
с ошибкой, не превышающей половины
данного отрезка
![]() .
.
