Яблонский Д10 вариант 20 / D10_v20

З а д а н и е Д.10. Применение теоремы об изменении кинетической энергии к изучению движения механической системы

Механическая система сил под действием сил тяжести приходит в движение из состояния покоя; начальное положение показано на рисунке. Учитывая сопротивление качению тела 3, катящегося без скольжения, пренебрегая другими силами сопротивления, массами нитей, предполагаемых нерастяжимыми, массами звеньев АВ, ВС и ползуна В определить скорость тела 1 в тот момент, когда пройденный им путь станет равным s.

Дано: – масса груза 1, и – массы тел 2 и 3, см, см – радиусы тел 2 и 3, см – радиус инерции тела 2 относительно горизонтальной оси, проходящей через центр тяжести, град – угол наклона плоскости к горизонту, – коэффициент трения скольжения, см – коэффициент трения качения, м, , .

Решение:

Применим теорему об изменении кинетической энергии системы :

, (1)

где T и T₀ – кинетическая энергия системы в начальном и конечном положениях; – сумма работ внешних сил, приложенных к системе, на перемещение системы из начального положения в конечное; – сумма работ внутренних сил системы на том же перемещении.

Для рассматриваемых систем, состоящих из абсолютно твердых тел, соединяемых нерастяжимыми нитями и стержнями,

.

Т.к. в начальном положении система находится в покое, то . Следовательно, уравнение (1) принимает вид:

.

Напишем кинематические соотношения между скоростями и перемещениями точек системы, т.е. уравнения связей, при этом скорости и перемещения выразим соответственно через скорости и перемещения груза 1.

Скорость точки D блока 2:

,

,

- угловая скорость блока 2,

, ,

,

.

После интегрирования (при нулевых начальных условиях):

.

Когда груз 1 пройдет путь , блок 2 повернется на угол :

.

При этом повороте блока 2 на 180⁰ его точка А₀ перейдет в конечное положение А и шатун А₀В₀ перейдет в конечное положение АВ. Каток 3 переместится влево при повороте блока 2 на угол и вправо при повороте блока еще на . Значит, конечное положение катка совпадет с начальным.

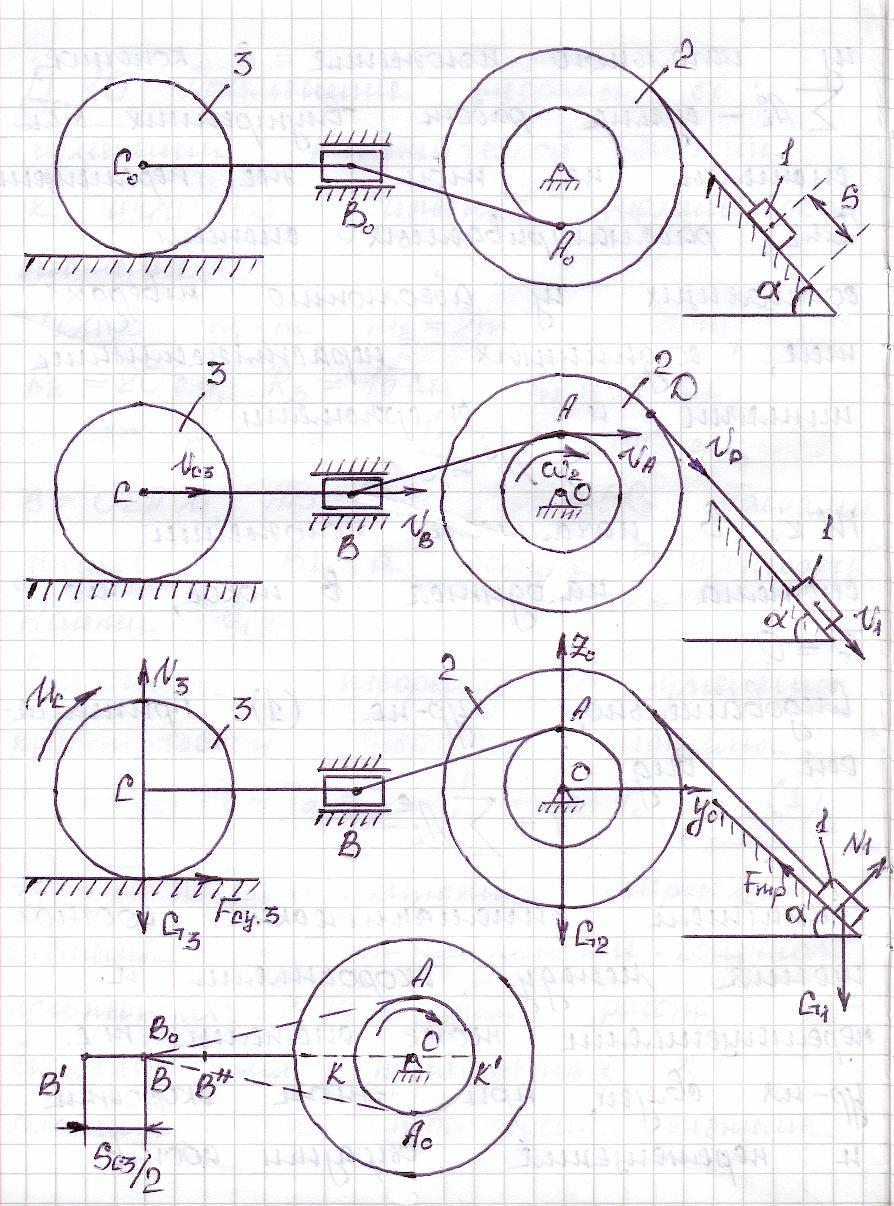
Кинетическая энергия системы:

.

Кинетическая энергия груза 1, движущаяся поступательно:

Кинетическая энергия тела 2, вращающегося вокруг оси 0x :

,

где – момент инерции.

.

Кинетическая энергия катка 3, совершающего плоско-параллельное движение:

- скорость центра масс С₃ катка, - момент инерции, - угловая скорость.

,

.

Скорость точки А:

,

.

Тогда:

,

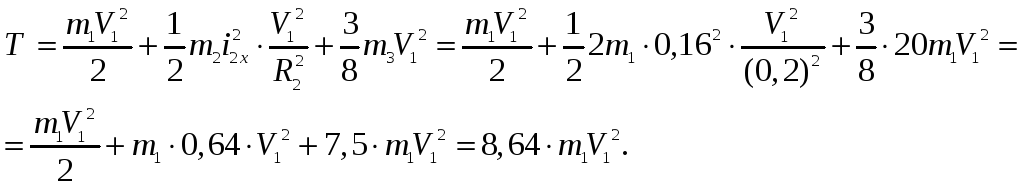
Найдем сумму работ всех внешних сил, приложенных к системе, на заданном перемещении:

– работа сил тяжести :

,

– работа сил трения скольжения :

,

– работа пары сил сопротивления качению катка 3:

, где,

его угол поворота:

.

Работу пары сил сопротивления вычисляем как сумму работ этой пары при качении катка 3 влево при повороте на угол и качении вправо, когда тело 2 повернется на угол .

Перемещение центра тяжести С₃ катка 3 равно перемещению ползуна В влево и вправо:

,

,

т.к. , то:

,

,

,

.

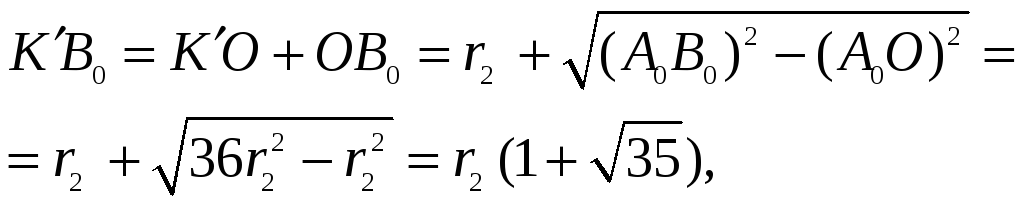
Работа пары сил сопротивления качению:

.

Сумма работ внешних сил:

,

,

,

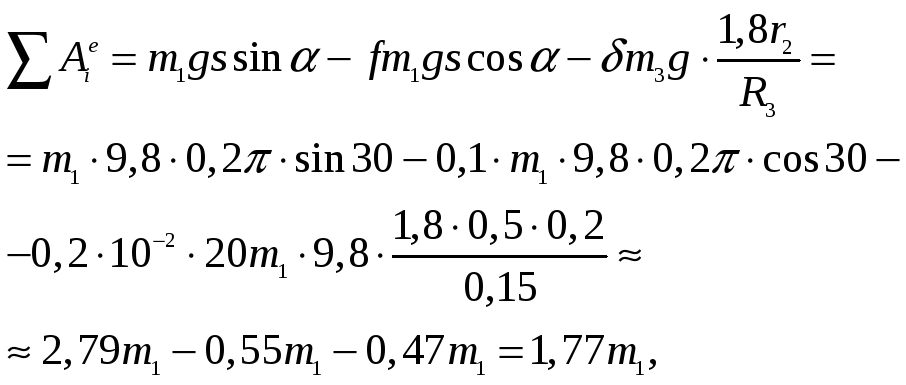
м/с.