Вариант № 21

1. Привести двойной интеграл к повторным интегралам двумя способами, если область интегрирования D:

2. Используя двойной интеграл вычислить площадь плоской фигуры, ограниченной указанными линиями и найти массу этой фигуры плотности

3. Построить область и вычислить в полярных координатах.

4. Найти массу криволинейного стержня , если , плотности .

5. Вычислить криволинейный интеграл вдоль линии от точки до точки N(0;0).

6. Найти массу тела, ограниченного поверхностями: , , , плотности .

7. Вычислить объем тела, ограниченного поверхностями , (внутри цилиндра).

Вариант № 22

1. Привести двойной интеграл к повторным интегралам двумя способами, если область интегрирования D:

2. Используя двойной интеграл вычислить площадь плоской фигуры, ограниченной указанными линиями 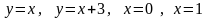и найти массу этой фигуры плотности

3. Построить область и вычислить в полярных координатах.

4. Найти массу отрезка прямой от точки А(0;3) до точки В(1;2), распределенную с плотностью .

5. Вычислить криволинейный интеграл вдоль дуги L кубической параболы от точки М(-1;-2) до точки N(0;0).

6. Найти массу тела, ограниченного поверхностями: , , , , , плотности .

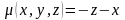7. Вычислить объем тела, ограниченного поверхностями , , , , .

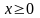Вариант № 23

1. Привести двойной интеграл к повторным интегралам двумя способами, если область интегрирования D:

2. Используя двойной интеграл вычислить площадь плоской фигуры, ограниченной указанными линиями и найти массу этой фигуры плотности

3. Построить область 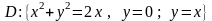и вычислить в полярных координатах.

4. Используя криволинейный интеграл, найти длину дуги кривой , если .

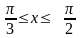5. Вычислить криволинейный интеграл вдоль дуги L параболы от точки М (0;0) до точки N (1;2).

6. Найти массу тела, ограниченного поверхностями: , , 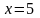, , плотности .

7. Вычислить объем тела, граничного поверхностями , , .

Вариант № 24

1. Привести двойной интеграл к повторным интегралам двумя способами, если область интегрирования D:

2. Используя двойной интеграл вычислить площадь плоской фигуры, ограниченной указанными линиями и найти массу этой фигуры плотности

3. Построить область 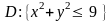и вычислить в полярных координатах.

4. Найти массу однородного криволинейного стержня где , распределенную с плотностью .

5. Вычислить криволинейный интеграл 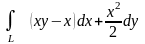вдоль дуги L кривой от точки А(0;0) до точки N(1;2).

6. Найти массу тела, ограниченного поверхностями: , , , , , плотности .

7. Вычислить объем тела, граничного поверхностями , , .

Вариант № 25

1. Привести двойной интеграл к повторным интегралам двумя способами, если область интегрирования D:

2. Используя двойной интеграл вычислить площадь плоской фигуры, ограниченной указанными линиями и найти массу этой фигуры плотности

3. Построить область и вычислить 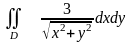в полярных координатах.

4. Используя криволинейный интеграл, найти длину дуги кривой , от точки до точки .

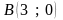5. Вычислить криволинейный интеграл вдоль дуги L параболы 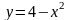от точки М (-2;0) до точки N(2;0).

6. Найти массу тела, ограниченного поверхностями: , , , плотности .

7. Вычислить объем тела, граничного поверхностями , , , .