Методы Оптимизации

65

1) Общая постановка задачи математического программирования.

Найти наибольшее и наименьшее значения y при ограничениях:

, i=1,2,…,k; , j=1,2,…,l;

Ограничения бывают типа равенств и неравенств.

2) Метод неопределенных множителей Лагранжа при поиске максимальных значений функций.

Найти экстремальные значения y при наличии ограничений типа равенств:

1) Образуем функцию Φ.

от n+k – переменных.

2) Ищем экстремум функции Ф.

3) Пусть M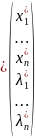 - точка установленного экстремума,

тогда М*= - точка установленного экстремума функции Ф.

2 этапа решения задач:

1) ищется условие оптимальности

2) технический этап – решение уравнений

1-ый способ общий, 2-ой не всегда реализуем.

3) Линейный функционал.

Переменная величина I называется функционалом, зависящим от функции y=y(x), что обозначается так: 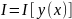, если каждой функции из некоторого класса функций соответствует значение I, т.е. имеет место соответствие: функции соответствует число I.

Линейным функционалом называется функционал , удовлетворяющий условиям:

1) , где с – произвольная постоянная

2)

4) Понятие вариации функционала.

Переменная величина I называется функционалом, зависящим от функции y=y(x), что обозначается так: , если каждой функции из некоторого класса функций соответствует значение I, т.е. имеет место соответствие: функции соответствует число I.

Приращением или вариацией функционала называется разность между двумя функциями . При этом предполагается, что меняется произвольно в некотором классе функций.

Если приращение функционала можно представить как

, где – вариация аргумента, - линейный по отношению к функционал, - максимальное значение и при , то линейная по отношению к часть приращения функционала, т.е. , называется вариацией функционала и обозначается .

Вариация функционала – главная линейная по отношению к ) часть приращения функционала.

5) Вычисление вариации функционала.

Порядок вычисления вариации функционала:

1. Заменяем аргумент: , где – вариация аргумента;

2. Вычисляем частную производную по ;

3. В полученном выражении полагаем , находим вариацию функционала

6) Постановка задачи Эйлера.

Задача – провести через две точки оптимальную кривую. В задаче Эйлера формируется критерий оптимальности:

Для задания критерия выбираем функцию от трех вещественных аргументов: или 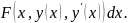Выполнив преобразования аргументов, получим функцию от одного вещественного аргумента.

Итак, нужно выбрать такую кривую, которая является экстремумом от функционала.

Условие экстремума: одинаковый знак приращения при изменении аргумента, т.е. .

7) Уравнение Эйлера.

Исследуем на экстремум функционал: для решения задачи Эйлера. Для начала найдем вариацию функционала по трем этапам (см. вопрос №5). Получим:

. Полученный функционал является линейным. Теперь применим условие экстремума ( ): - это основная лемма вариационного исчисления, т.е. если мы имеем некий функционал равный нулю при любом , то и . Нужно привести условие экстремума к виду этой леммы, т.е. при Преобразуем выражение (1) и получим:

Мы получили дифференциальное уравнение относительно Это уравнение Эйлера, которое позволяет решить задачу Эйлера. Интегральные кривые уравнения Эйлера называют экстремалями.