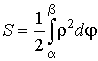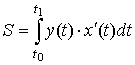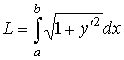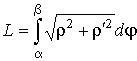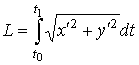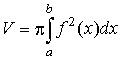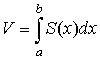- •1.1. Определители (детерминанты)
- •1.2. Матрицы
- •1.3. Системы линейных уравнений
- •3.1. Линейные образы
- •3.1.1. Прямая на плоскости
- •3.1.2. Плоскость в пространстве
- •3.1.3. Прямая в пространстве
- •3.2. Кривые второго порядка
- •3.3. Поверхности второго порядка
- •3.4. Преобразование координат
- •3.4.1. Преобразование координат на плоскости
- •3.4.2. Преобразование координат в пространстве
- •5.2. Основные элементарные функции
- •5.3. Теория пределов
- •5.4. Непрерывность функции
- •6.1. Определение производной
- •6.2. Основные правила дифференцирования
- •6.3. Производные основных элементарных функций
- •6.4. Гиперболические функции
- •6.5. Производные высших порядков и формула Тейлора
- •6.6. Исследование функций
- •7.1. Неопределенный интеграл
- •7.1.1. Определения и свойства
- •7.1.2. Основные методы интегрирования
- •7.1.3. Таблица интегралов
- •7.2. Определенный интеграл
- •7.2.1. Определения и свойства
- •7.2.2. Приложения определенного интеграла
7.2. Определенный интеграл
7.2.1. Определения и свойства
,
где
![]()
Свойства определенного интеграла
Интеграл от суммы или разности двух функций:
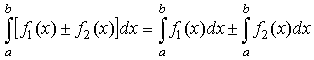 .
.Внесение или вынесение постоянного множителя за знак интеграла:
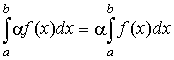 .
.
Свойство аддитивности:
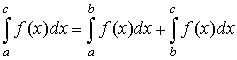 .
.Неотрицательность интеграла: если
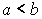 ,
,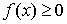 ,
то
,
то
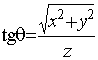 .
.Сохранение неравенства: если
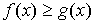 и
и
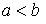 ,
то
,
то
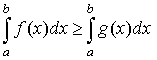 .
.Теорема о среднем:
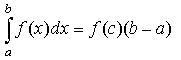 ,
где
,
где
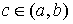 ,
-
непрерывна на
,
-
непрерывна на
 .
.Формула Ньютона-Лейбница:
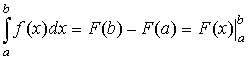 ,
где
,
где
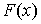 -
первообразная для
.
-
первообразная для
.Интегрирование по частям:
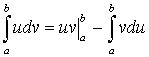 .
.Замена переменной:
а)
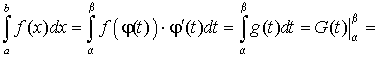
![]() ,
где
,
где
![]() ,
,
![]() ,
,
![]() и
непрерывна
на
и
непрерывна
на
![]() ,
а
,
а
![]() непрерывна
и монотонна на
непрерывна
и монотонна на
![]()
б)
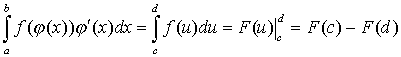 ,
где
u=
(x), c=
(a), d=
(b).
,
где
u=
(x), c=
(a), d=
(b).
7.2.2. Приложения определенного интеграла
Характеристика |
Вид функции |
Формула |
площадь криволинейной трапеции |
в декартовых координатах |
|
площадь криволинейного сектора |
в полярных координатах |
|
площадь криволинейной трапеции |
в параметрической форме |
|
длина дуги кривой |
в декартовых координатах |
|
длина дуги кривой |
в полярных координатах |
|
длина дуги кривой |
в параметрической форме |
|
объём тела вращения |
в декартовых координатах |
|
объём тела с заданным поперечным сечением |
|
|