3.4. Відстань від точки до прямої

Відстань від точки М₀ (х₀; у₀) до прямої Ах + By + С = 0 знаходять за формулою

.

Задачі

1. Скласти канонічне рівняння прямої, що проходить через дану точку М₀ паралельно вектору , якщо:

1. М₀ (-4; 2), (2; -l); b) М₀ (4; 0), = 3 - 7 ;

c) M₀ (-l; 3), = 4 .

2. Записати параметричне рівняння кожної з даних прямих:

а) ; b) .

3. Скласти рівняння прямої, що проходить через точку М₀(-1;3) перпендикулярно вектору (2;-3).

4. Серед множини прямих А(х+3)+В(у-4)=0 знайти ту, яка перпендикулярна вектору = -5 + 3 .

5. Скласти рівняння прямої, що проходить через середину відрізка АВ, перпендикулярно до нього, якщо А(3;-2), В(5;-4).

6. Дано ∆АВС з вершинами А(3;4), В(2;5), С(7;8). Скласти рівняння прямої, що проходить через точку В перпендикулярно медіані BD (точка D належить АС).

7. Знайдіть кутовий коефіцієнт прямої, що проходить через точки М₁(-2;3) і M₂(5;-1).

8. Знайти кутовий коефіцієнт і початкову ординату прямої

3х+2у-6=0.

9. Скласти рівняння прямої, що проходить через точку М₀(-3;2) і утворює з додатнім напрямом осі Ох кут .

10. Із пучка прямих, визначених рівнянням y+2=k(x-5), знайти ту, яка проходить через точку А(1 ;6).

11. Дано координати вершин ∆АВС: А(2;4), В(6;3), С(4;-3). Скласти рівняння медіани AD.

12. Скласти рівняння прямої, якщо точка М(2;3) є серединою її відрізка, розташованого між осями координат.

13. Скласти рівняння прямої, що утворює з віссю ОХ кут = 30° і проходить через точку А(-1;1).

14. Знайти пряму, паралельну прямій 3х-7у+11=0, яка проходить через точку А(0;3).

15. Знайти площу трикутника, обмеженого прямою х-у+3=0 і осями координат.

16. Довести, що прямі 3х-2у-1=0 і 2х+5у-12=0 перетинаються, і знайти їх точку перетину.

17. Знайти кут між прямими: 7х-у-2=0 і х-у+3=0.

18. Знайти кут між прямими: 2х-у-4=0 і у= х + 4.

19. При якому значенні а пари прямих паралельні; перпендикулярні. Прямі задані рівняннями:

a) 3х-2у+11=0 і ах-4у+3=0;

b) 7х-2у+9=0 і ах+у-3=0.

20. Знайти кут між прямими 2х-3у+5=0 і х+2у+2=0.

§4. Лінії другого порядку

4.1. Коло.

Рівняння (х — х₀)² + (у — y₀)² = R² визначає коло (рис. 4.1) з центром у точці С (х₀, у₀) і радіусом R. Зокрема, якщо центром кола є початок координат (х₀ = 0, у₀ = 0), то рівняння кола має вигляд

x² + y² = R².

Рис. 4.1

4.2. Еліпс

Канонічне рівняння еліпса (рис. 4.2) має вигляд , де . Відстані між вершинами називаються осями еліпса: велика (фо­кальна) вісь А₂А₁ = 2а і мала вісь В₂В₁ = 2b, відстань між фокусами F₂F₁ = 2с; a, b — півосі еліпса.

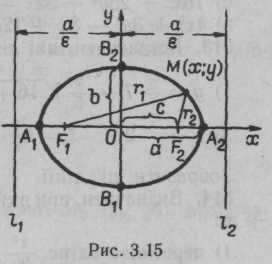
Рис. 4.2

Ексцентриситет еліпса визначається рівністю , очевидно, 0 < < 1.F₁M = r₁ і F₂M = r₂ — фокальні радіуси точки М. Прямі x = ± - директриси еліпса.

Рівняння дотичної до еліпса у точці М₀ (х₀; у₀) має вигляд . Еліпс з центром у точці С(х₀; у₀) задається рівнянням .

Задачі

1. Перевірити, чи є колом лінія, задана рівнянням: х²+у²-4x-6y+l=0. Знайти її центр і радіус.

2. Записати рівняння кола, якщо точки А(-1;4) і В(3;2) є кінцями його діаметра.

3. Скласти рівняння кола, діаметром якого є відрізок прямої

4х - 3у + 12 = 0, і який (діаметр) міститься між осями координат.

4. Скласти рівняння кола, що дотикається до осі абсцис у точці A(2;0) і проходить через точку В(-1;3).

5. Знайти координати центра і радіус кола:

a) х² + у² + 6х – 10у + 13 = 0;

b) х² + у² +12у - 13 = 0;

с) 9х² + 9у² +12х - 54у - 95 = 0;

6. Скласти рівняння кола, що проходить через центри кіл:

х²+у²+6x+8y=0 і х²+у²+2х-12у+1=0.

7. Скласти рівняння прямої, що проходить через три точки: А(0;2), В(1;1) і С(2;-2).

8. Скласти рівняння кола з центром в точці (2;2), яке дотикається до прямої 3х+у–18=0.

9. Скласти рівняння кола, описаного навколо трикутника, вершинами якого є точки А(0;1), В(-2;0), С(0;-1).

10. Скласти рівняння кола, діаметром якого є спільна хорда кіл:

х²+у²+4x-4y+2=0 і x²+y²-2x+2y-l4=0.

11. Скласти канонічне рівняння еліпса, який проходить через точки М₁(3,2) М₂ 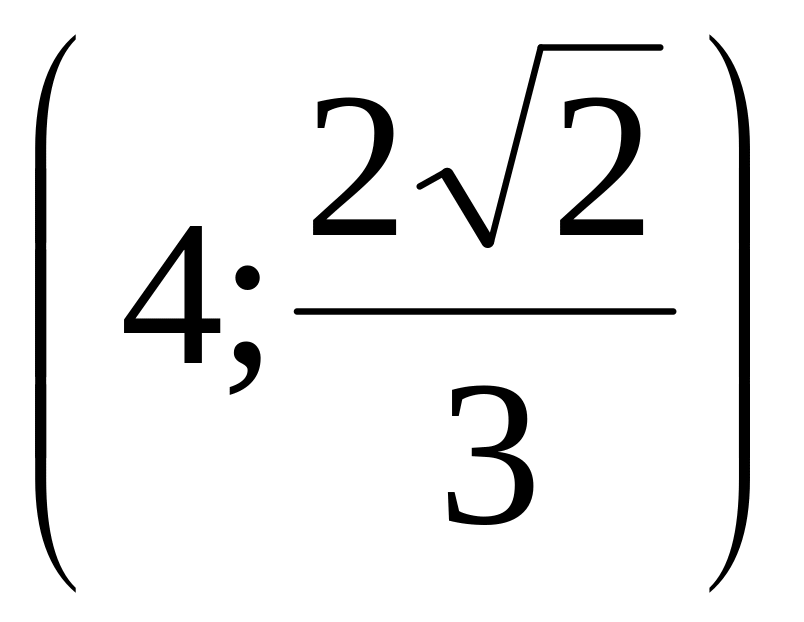, якщо його фокуси лежать на осі Ох симетрично початку координат.

12. Скласти канонічне рівняння еліпса, фокуси якого знаходяться на осі Ох, симетрично початку координат, якщо відстань між фокусами дорівнює 14, а ексцентриситет дорівнює .

13. Скласти канонічне рівняння еліпса, якщо задані його вершини (0;3) і (0;-3) і відстань між фокусами дорівнює 8.

14. Знайти довжини осей, координати фокусів і ексцентриситет еліпса:

16х²+25у²=400.

15. Скласти канонічне рівняння еліпса з ексцентриситетом =0,28 і фокусами: (±7;0).

16. Побудувати еліпс х²+4у²=16. Знайти його фокуси і ексцентриситет.

17. Еліпс, фокуси якого розташовані на осі абсцис, симетрично відносно початку координат, проходить через точку М(1;1) та має ексцентриситет . Скласти рівняння еліпса.

18. Визначити ексцентриситет еліпса, якщо його малу вісь видно з фокуса під прямим кутом.

19. Скласти рівняння еліпса, знаючи, що його велика вісь дорівнює 26 та фокуси F₁(-10;0), F₂(14;0).

20. Знайти точки перетину еліпса з прямою 2х–у–9=0.