
- •Видання здійснено за фінансової підтримки громадської організації „Рада батьків Черкащини”
- •Рекомендовано до друку рішенням Розповсюдження та тиражування
- •Глава 1. Елементи лінійної алгебри
- •§1. Визначники Визначники другого і третього порядків
- •IV. Обчислити визначники накопиченням нулів у рядку чи стовпці
- •V. Розв’язати нерівність
- •§2. Mатриці. Дії над матрицями. Обернена матриця. Ранг матриці
- •2.1. Дії над матрицями
- •2.2. Обернена матриця
- •2.3. Ранг матриці
- •IV. Розв’язати матричні рівняння
- •V. Визначити ранг матриці
- •§3. Системи лінійних рівнянь
- •3.1. Розв'язування систем лінійних рівнянь за формулами Крамера
- •3.2. Матричний метод розв'язування систем лінійних рівнянь
- •3.3. Розв'язування систем лінійних рівнянь методом Гауса
- •Глава 2. Елементи векторної алгебри та аналітичної геометрії
- •§1 Вектори. Лінійні операції над векторами
- •§2. Скалярний добуток векторів. Проекції вектора. Розкладання вектора за базисом. Лінійна залежність векторів
- •§3. Пряма на площині
- •3.1. Різні види рівнянь прямої на площині
- •3.2. Загальне рівняння прямої та його дослідження. Пучок прямих
- •3.3. Кут між двома прямими. Умови паралельності і перпендикулярності двох прямих
- •3.4. Відстань від точки до прямої
- •§4. Лінії другого порядку
- •4.1. Коло.
- •4.3. Гіпербола, парабола
- •§5. Площина у просторі
- •5.1. Загальне рівняння площини та його дослідження
- •5.2. Різні види рівнянь площини
- •5.3. Кут між двома площинами
- •Відповіді
- •Глава 1
- •§2. I. 1. . 2. Матриці не узгоджені. 3. .
- •Глава 2
- •Список рекомендованої літератури
- •Вища математика
- •18000, М. Черкаси, вул. Смілянська, 2
§2. Скалярний добуток векторів. Проекції вектора. Розкладання вектора за базисом. Лінійна залежність векторів
Лінійною
комбінацією векторів
![]() з дійсними коефіцієнтами
з дійсними коефіцієнтами
![]() називається
довільний вектор виду
називається
довільний вектор виду
![]() .
.
Якщо вектор поданий у вигляді лінійної комбінації
деяких векторів, то кажуть, що він розкладений за цими векторами.
Вектори
називаються лінійно
залежними,
якщо існують такі числа
,
що
![]() і
і
![]() .
Якщо рівність
справджується лише при
.
Якщо рівність
справджується лише при
![]() ,
то вектори
називаються лінійно
незалежними.
,
то вектори
називаються лінійно
незалежними.
Два колінеарні вектори — лінійно залежні, а два неколінеарні — лінійно незалежні.
Три компланарні вектори — лінійно залежні, а три некомпланарні вектори —лінійно незалежні. Чотири вектори в тривимірному просторі завжди лінійно залежні.
Базисом
![]() векторів на площині називається
упорядкована пара лінійно незалежних
(неколінеарних) векторів
векторів на площині називається
упорядкована пара лінійно незалежних
(неколінеарних) векторів
![]() і
і
![]() .
Всякий вектор
.
Всякий вектор
![]() ,
компланарний векторам
і
,
компланарний векторам
і
![]() ,
які утворюють базис, можна подати у
вигляді суми
,
які утворюють базис, можна подати у
вигляді суми
![]() .
Числа
та
.
Числа
та
![]() називають координатами
вектора
у базисі
і пишуть
називають координатами
вектора
у базисі
і пишуть
![]() ,
а саму суму — розкладом вектора за
цим базисом.
,
а саму суму — розкладом вектора за
цим базисом.
Базисом
![]() у просторі
називається упорядкована трійка лінійно
незалежних (некомпланарних) векторів.
Довільний вектор
простору можна розкласти за базисом
:
у просторі
називається упорядкована трійка лінійно
незалежних (некомпланарних) векторів.
Довільний вектор
простору можна розкласти за базисом
:
![]() ,
де
,
,
,
де
,
,
![]() — координати вектора
у цьому базисі:
— координати вектора
у цьому базисі:
![]() .
.
Скалярним
добутком векторів
![]() називається число, яке дорівнює добутку
модулів цих векторів на косинус кута
називається число, яке дорівнює добутку
модулів цих векторів на косинус кута
![]() між ними:
між ними:
![]() .
.
Скалярний
добуток позначають також
![]() і
і
![]() .
.
Геометричні властивості скалярного добутку
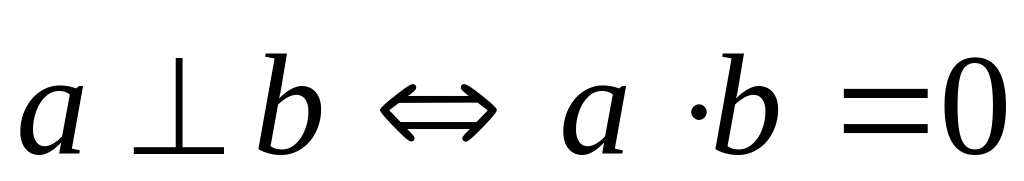 (умова
перпендикулярності векторів);
(умова
перпендикулярності векторів); ;
; ;
; .
.
Алгебраїчні властивості скалярного добутку
 ;
; ;
; ;
; .
.
Якщо
вектори задано своїми координатами
![]()
![]() ,
то скалярний добуток
,
то скалярний добуток
![]() ,
,
а
кут
![]() між векторами
між векторами
![]() знаходять за формулою
знаходять за формулою
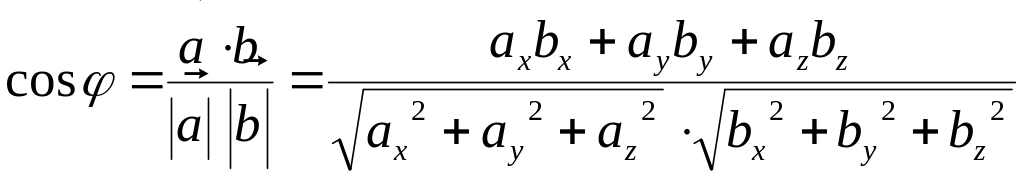 .
.
Задачі
Знайти проекцію вектора
 на вісь, напрямок якої співпадає з
напрямком вектора
на вісь, напрямок якої співпадає з
напрямком вектора
 ,
якщо
,
якщо
 і
і
 .
.Знайти координати точки В, яка є кінцем вектора
 ,
якщо початок співпадає точкою А(1;4;-7).
,
якщо початок співпадає точкою А(1;4;-7).
Довести, що точки А(-1;2;3), В(2;-1;1), С(1;-3;-1) і D(-5;3;3) є вершинами трапеції.
Задано три вектори
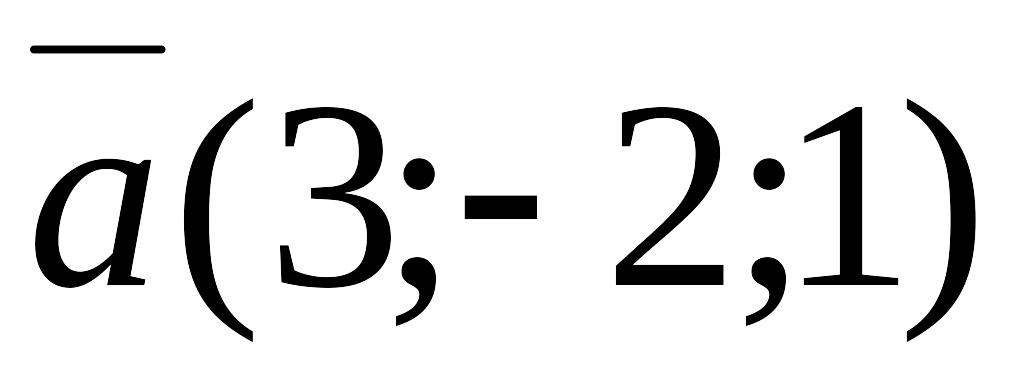 ,
,
 ,
,
 .
Розкласти вектор
.
Розкласти вектор
 за базисом
за базисом
 і
.
і
.Задані точки: А(0;-1;2) і В(-1;1;4). Знайти координати, довжину і напрямні косинуси вектора .
Чи може вектор утворювати з осями координат кути
 60°,
60°,
 = 30°?
= 30°?Знайти вектор
 ,
колінеарний вектору
,
колінеарний вектору
 .
.Знайти скалярний добуток векторів
 і
і
 ,
якщо
,
якщо
 ;
;
 ;
;
 .
.Знайти довжину вектора
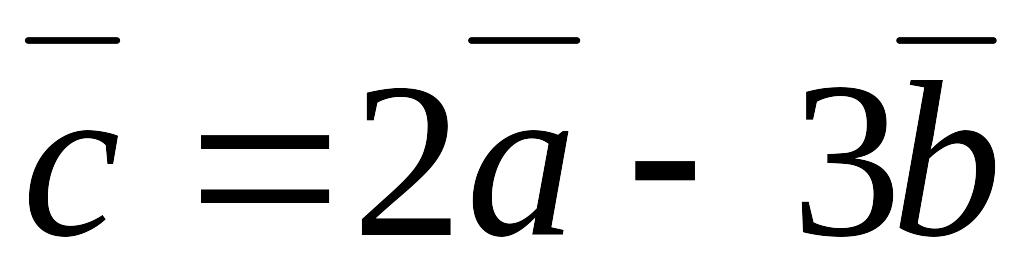 ,
якщо
;
,
якщо
;
 ,
а кут між векторами
і
дорівнює
,
а кут між векторами
і
дорівнює
 .
.Вектори і взаємно перпендикулярні, а вектор
 утворює з ними кути рівні
утворює з ними кути рівні
 ,
знаючи, що
,
знаючи, що
 ,
,
 ,
,
 .
Обчислити
.
Обчислити
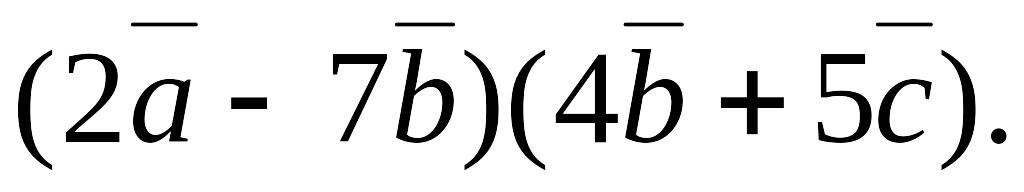
При якому значенні m вектори
 і
і
 перпендикулярні?
перпендикулярні?Представити вектор
 як лінійну комбінацію векторів
і
в кожному випадку, якщо:
як лінійну комбінацію векторів
і
в кожному випадку, якщо:
а)
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
b)
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
c)
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Знайти
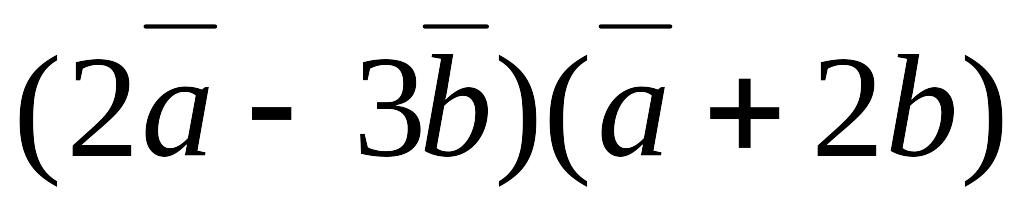 ,
якщо
,
якщо
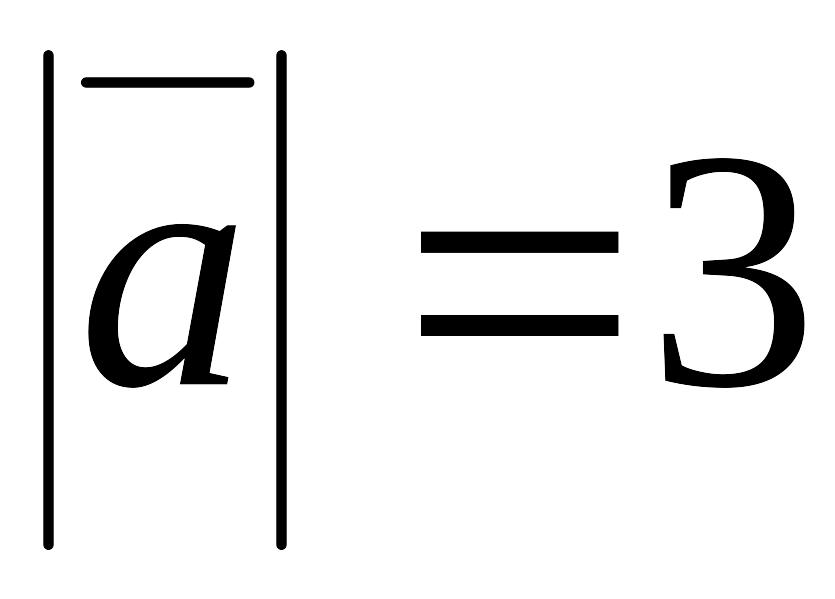 ,
,
,
,
 = 60°.
= 60°.Знайти модуль вектора
 ,
якщо
,
якщо
 ,
,
 ,
кут між векторами
і
дорівнює 120°.
,
кут між векторами
і
дорівнює 120°.Вектори і утворюють кут
 .
Відомо, що
.
Відомо, що
 ,
,
 .
Знайти кут
між векторами
.
Знайти кут
між векторами
 i
i
 .
.Кут між векторами і дорівнює 60°,
 ,
,
 .
Знайти
.
Знайти
 і
і
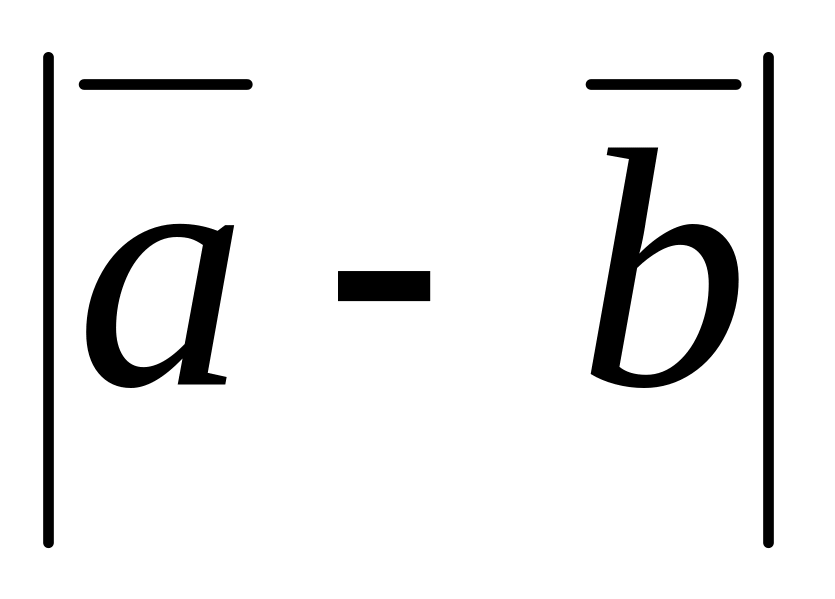 .
.Кут між векторами і
 дорівнює 120°. Знайти:
дорівнює 120°. Знайти:
а)
![]() ;
;
b)
![]() ;
;
c)
![]() ;
;
d)
![]() ;
;
e)
![]() .
.
Дано точки A(-3;0;-2), B(5;-2;l), C(2;6;-l), D(l;3;-3). Довести, що прямі АВ та CD взаємно перпендикулярні.
Дано вершини трикутника А(0;0;5), В(5;-2;1), С(2;6;1). Знайти проекцію вектора на
 .
.Дано вершини трикутника А(0;0;5), В(5;-2;1), С(2;6;1). Знайти кути трикутника.
