Глава 2. Елементи векторної алгебри та аналітичної геометрії

§1 Вектори. Лінійні операції над векторами

В ектором називається напрямлений відрізок. Якщо початок вектора міститься в точці А, а кінець — у точці В, то вектор позначають так: (рис. 2.1). Вектор позначають також малою буквою латинського алфавіту із стрілочкою над нею або жирним шрифтом без стрілочки: , с.

Довжина вектора або називається його модулем і позначається або .

Вектор, довжина якого дорівнює 0 (тобто початок якого збігається з кінцем), називається нульовим; позначається .

Одиничним називається вектор, довжина якого дорівнює одиниці.

Одиничний вектор, який має той самий напрям, що й вектор , позначається .

Вектори, які лежать на паралельних прямих (або на одній і тій самій прямій), називаються колінеарними.

Вектори, які лежать на паралельних площи­нах (або на одній і тій самій площині), назива­ються компланарними.

Вектори називаються рівними між собою, якщо вони колінеарні, однаково напрямлені і рівні за модулем.

Вектор, колінеарний даному вектору , рівний йому за модулем і протилежно напрямлений, називається протилежним вектором для вектора і позначається - .

Радіусом-вектором точки М відносно точки О називається вектор .

Сумою + двох векторів і називається вектор, напрямлений з початку вектора а в кінець вектора за умови, що кінець вектора і початок вектора збігаються (рис. 2.2, а). Сума кількох векторів — це вектор, який замикає ламану, побудовану з даних векторів (рис. 2.2, б).

Рис. 2.2.

Різницю - векторів , розглядають як суму векторів та — (рис. 2.3).

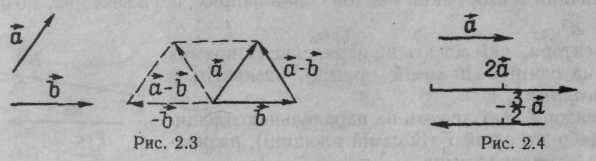
Рис. 2.3 Рис.2.4

Добутком дійсного числа на вектор називається вектор = = , довжина якого | | = | | | |, а напрям збігається з напрямом вектора при > 0 і протилежний йому при < 0 (рис. 2.4). Якщо = 0, то = .

Задачі

1. Як повинні бути розміщені вектори і , щоб .

2. ABCD - паралелограм. М і N - середини його сторін. Розкласти вектор за векторами = і = .

3. Вектори = і = є діагоналями паралелограма ABCD. Виразити вектори , , і через і .

4. В ∆АВС проведена медіана AD. Точка D - середина ВС.

Довести, що + = 2 .

5. У ∆АВС, точка О - точка перетину медіан. Довести, що .

6. За даними векторами і , побудувати кожний з таких векторів: а) + ; б) - ; в) - ; г) - - .

7. У ∆АВС проведено медіани AD, BM, CN. Довести рівність + + = .

8. Яку умову мають задовольняти вектори і , щоб вектор + ділив навпіл кут між векторами і .

9. Три вектори = , = і = є сторонами трикутника. Через вектори , і виразити вектори, що збігаються з медіанами трикутника , і .

10. У ромбі ABCD дано вектори-діагоналі = і = . Розкласти за цими векторами усі вектори-сторони ромба: , , і .

11. У трикутнику ABC проведені медіани AD, BE і СР. Записати вектори , і у вигляді лінійної комбінації векторів і .

12. Нехай ABC - довільний трикутник, а Е і F - середини сторін АВ і ВС. Виразити вектори , і через = і = .

13. На площині трикутника ABC знайти таку точку, щоб сума векторів, які направлені із цієї точки до вершин трикутника, дорівнювала нулю.

14. У трикутнику ABC пряма AM є бісектрисою кута ВАС, причому точка М лежить на стороні ВС. Знайти AM, якщо = , = .

15. Дано паралелограм ABCD. Точка М лежить на стороні CD. Знайти суму векторів:

1. + ;

2. + ;

3. (- ) + DM;

4. + BM.

15. Дано паралелограм ABCD і довільна точка О простору.

Довести, що + = + .

15. Точки Е і F є серединами сторін АВ і CD чотирикутника (на площині або в просторі). Довести, що .

16. Дано трикутник ABC. На стороні ВС розташована точка М так, що . Знайти , якщо = , = .

17. На стороні AD паралелограма ABCD відкладений відрізок , а на діагоналі - відрізок . Довести, що вектори і колінеарні і знайти відношення .

18. Довести, що сума векторів, які направлені з центра правильного многокутника до його вершин, дорівнює .