
- •Видання здійснено за фінансової підтримки громадської організації „Рада батьків Черкащини”
- •Рекомендовано до друку рішенням Розповсюдження та тиражування
- •Глава 1. Елементи лінійної алгебри
- •§1. Визначники Визначники другого і третього порядків
- •IV. Обчислити визначники накопиченням нулів у рядку чи стовпці
- •V. Розв’язати нерівність
- •§2. Mатриці. Дії над матрицями. Обернена матриця. Ранг матриці
- •2.1. Дії над матрицями
- •2.2. Обернена матриця
- •2.3. Ранг матриці
- •IV. Розв’язати матричні рівняння
- •V. Визначити ранг матриці
- •§3. Системи лінійних рівнянь
- •3.1. Розв'язування систем лінійних рівнянь за формулами Крамера
- •3.2. Матричний метод розв'язування систем лінійних рівнянь
- •3.3. Розв'язування систем лінійних рівнянь методом Гауса
- •Глава 2. Елементи векторної алгебри та аналітичної геометрії
- •§1 Вектори. Лінійні операції над векторами
- •§2. Скалярний добуток векторів. Проекції вектора. Розкладання вектора за базисом. Лінійна залежність векторів
- •§3. Пряма на площині
- •3.1. Різні види рівнянь прямої на площині
- •3.2. Загальне рівняння прямої та його дослідження. Пучок прямих
- •3.3. Кут між двома прямими. Умови паралельності і перпендикулярності двох прямих
- •3.4. Відстань від точки до прямої
- •§4. Лінії другого порядку
- •4.1. Коло.
- •4.3. Гіпербола, парабола
- •§5. Площина у просторі
- •5.1. Загальне рівняння площини та його дослідження
- •5.2. Різні види рівнянь площини
- •5.3. Кут між двома площинами
- •Відповіді
- •Глава 1
- •§2. I. 1. . 2. Матриці не узгоджені. 3. .
- •Глава 2
- •Список рекомендованої літератури
- •Вища математика
- •18000, М. Черкаси, вул. Смілянська, 2
IV. Розв’язати матричні рівняння
1.
![]() 2.
2.![]() .
.
3.
![]() 4.
4.
![]()
5.

V. Визначити ранг матриці
1.
![]() 2.
2.
![]() .
.
3.
 4.
4.
![]() .
.
5.
 6.
6.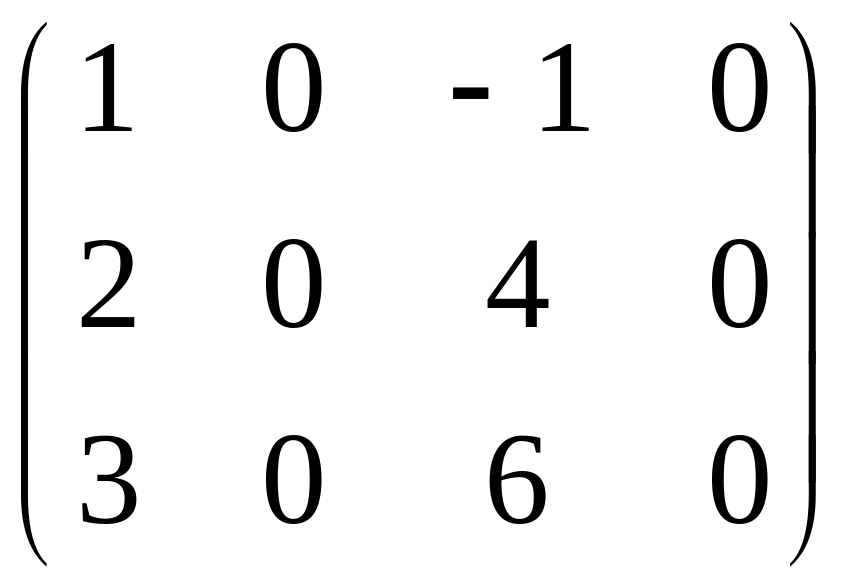 .
.
7.
 8.
8. .
.
9.
 10.
10. .
.
11.
 12.
12. .
.
13.
 14.
14. .
.
§3. Системи лінійних рівнянь
3.1. Розв'язування систем лінійних рівнянь за формулами Крамера
Система двох лінійних рівнянь з двома невідомими має вигляд
![]()
Введемо позначення:
![]()
Якщо
![]() ,
то система має єдиний розв'язок і
справедливі формули Крамера
,
то система має єдиний розв'язок і
справедливі формули Крамера
![]() .
.
Якщо
![]() ,
,
![]() або
або
![]() ,
то система не має розв'язків. Якщо
,
то система не має розв'язків. Якщо
![]() ,
то система має безліч розв'язків.
,
то система має безліч розв'язків.
Система трьох лінійних рівнянь з трьома невідомими має вигляд
![]()
Аналогічно введемо позначення:
 ,
,  ,
,
 ,
,  .
.
Якщо , то система має єдиний розв'язок і його знаходять за формулами Крамера
![]()
Якщо
,
а одне з чисел
![]() не дорівнює нулю, то система розв'язку
не має. При
не дорівнює нулю, то система розв'язку
не має. При
![]() система може бути
несумісною або
мати безліч розв'язків.
система може бути
несумісною або
мати безліч розв'язків.
Аналогічні формули Крамера справедливі для n лінійних рівнянь з n невідомими.
3.2. Матричний метод розв'язування систем лінійних рівнянь
Нехай задано систему n лінійних рівнянь з n невідомими
![]() (3.1)
(3.1)
Введемо матриці
 .
.
Тоді згідно з правилом множення матриць систему (3.1) можна записати одним матричним рівнянням з невідомою матрицею X:
АХ = В.
Якщо матриця А має обернену матрицю А-1, то
Х = А-1В.
Ця формула називається матричним записом розв'язку системи (3.1). Отже, щоб розв'язати систему рівнянь (3.1), достатньо знайти матрицю, обернену до матриці системи А, і помножити її на матрицю з вільних членів справа.
3.3. Розв'язування систем лінійних рівнянь методом Гауса
Нехай задано систему m лінійних рівнянь з n невідомими
![]() (3.2)
(3.2)
Метод Гауса — це метод послідовного виключення невідомих. За допомогою елементарних перетворень систему (3.2) приводять до системи вигляду
![]() (3.3)
(3.3)
Таку систему рівнянь називають східчастою або трапецієподібною.
1) Якщо система (3.3) містить рівняння виду 0 = bt і bt ≠ 0, то вона очевидно несумісна.
2) Якщо система (3.3) не містить рівнянь виду 0 = bt (bt ≠ 0), то вона має безліч розв'язків.
Назвемо невідомі х1, xk, xl ..., xs основними, а всі інші — вільними (якщо вони є). Надаючи вільним невідомим довільні значення і підставляючи їх у рівняння системи, з r-го рівняння знайдемо xs. Підставляючи це значення в перші r — 1 рівнянь і піднімаючись угору по системі, знайдемо всі основні невідомі. Оскільки вільні невідомі можуть набувати будь-яких значень, то система має безліч розв'язків.
3) Якщо r = n, то система (3.3) має трикутний вигляд і вільних невідомих не має. В цьому випадку система має єдиний розв'язок.
І. Розв’язати СЛР за формулами Крамера
1.
![]() 2.
2.
![]()
3.
 4.
4.

5.
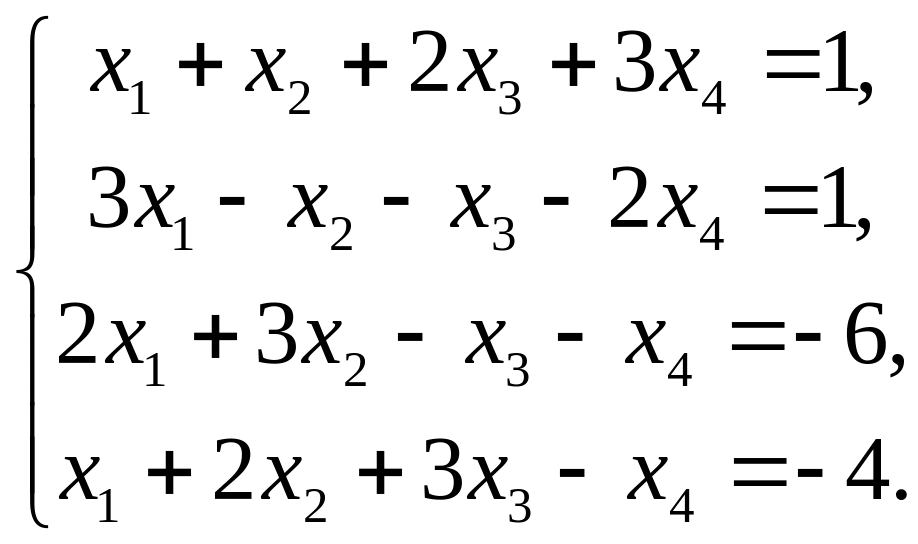 6.
6.

7.
 8.
8.

9.
 10.
10.

ІІ. Матричним методом розв’язати СЛР
1.
 2.
2.

3.
 4.
4.

5.
 6.
6.

7.
 8.
8.

9.
 10.
10.

ІІІ. Розв’язати СЛР методом Гаусса
1.
 2.
2.

3.
 4.
4.

5.
 6.
6.

7.
 8.
8.

9.
 10.
10.

11.
12.

13.
 14.
14.

