Яблонский С6 вариант 12

C-6. Приведение системы сил к простейшему виду.

Дана система сил ; модули точек приложения и направления этих сил указаны в табл. C6.1

Таблица C6.1

Размеры прямоуголного параллелипипеда, см

Силы системы

a

b

c

Модуль, Н

Точка приложения

направление

Модуль, Н

Точка приложения

направление

Модуль, Н

Точка приложения

направление

Модуль, Н

Точка приложения

направление

4

8

6

6

A

AE

20

F

FA

10

C

CK

8

D

DK

1. Определение главного вектора заданной системы сил. Заданная система сил показана на рис C6.1

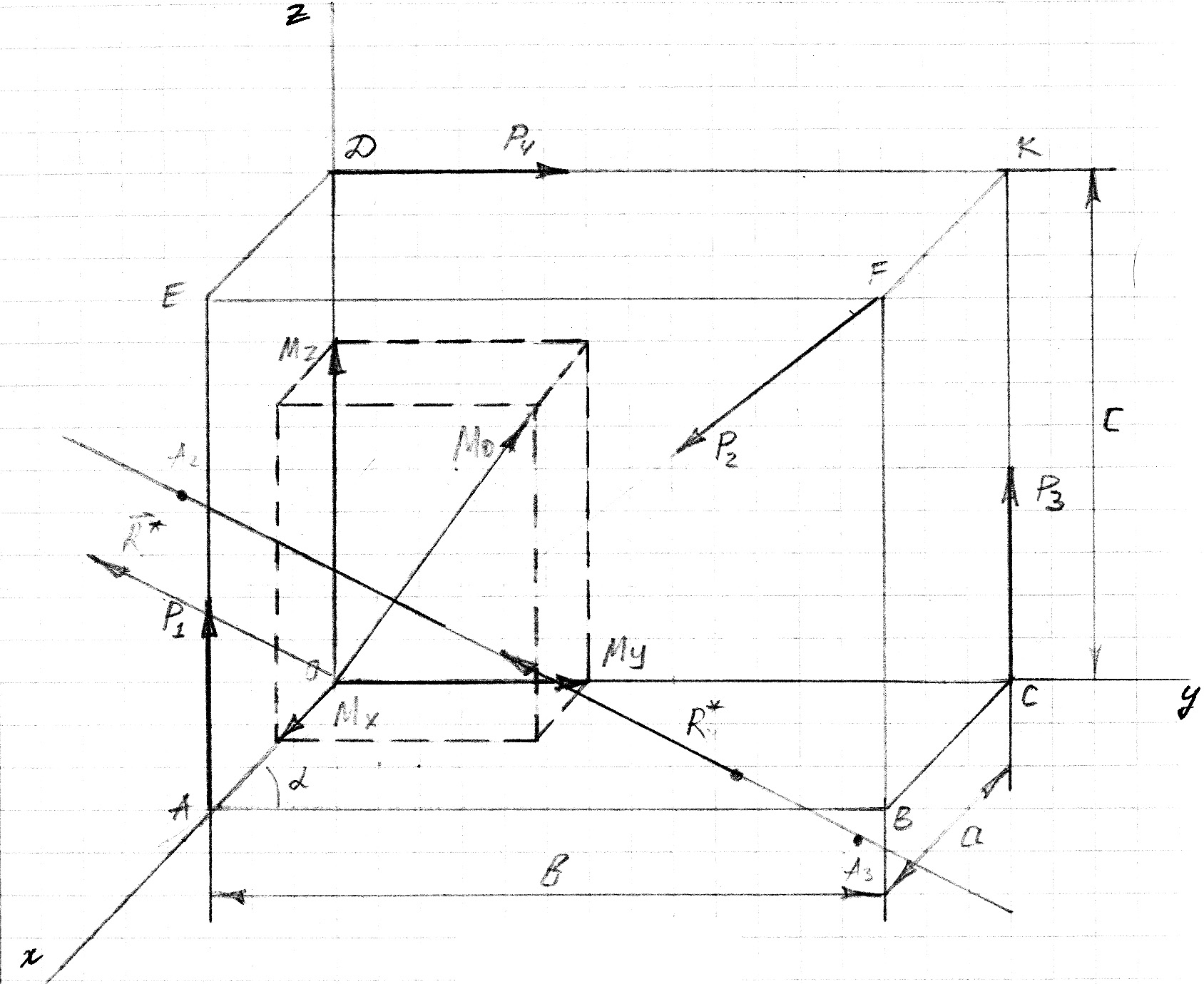
рис. C6.1

Предварительно определяем

Проекции главного вектора на оси координат:

X = 0 Н;

Y = P₄ – P₂∙cos α = –8 Н;

Z = P₁ + P₃ – P₂∙sin α =4 Н;

Модуль главного вектора:

;

Направляющие косинусы:

Главный вектор показан на рис. C6.1.

2. Определение главного момента заданной системы сил относительно центра О.

Главные моменты заданной системы сил относительно координатных осей:

M_X = P₃∙b – P₂∙ sin α∙6 – P₄∙c = 32 Н∙см

M_Y = (P₂∙ sin α – P₁)∙a = 24 Н∙см

M_Z = – P₂∙ cos α = –64 Н∙см

Модуль главного момента:

Направляющие косинусы:

3. Вычисление наименьшего главного момента заданной системы сил.

M* = (M_X*X + M_Y*Y + M_Z*Z)/R^* = – 50,337 Н*см

4. Т.к. и , то система приводится к динаме. Составим уравнение главной оси:

Из этих трех уравнений независимыми являются только два. Подставляя в два из этих уравнений найденные числовые значения величин, находим:

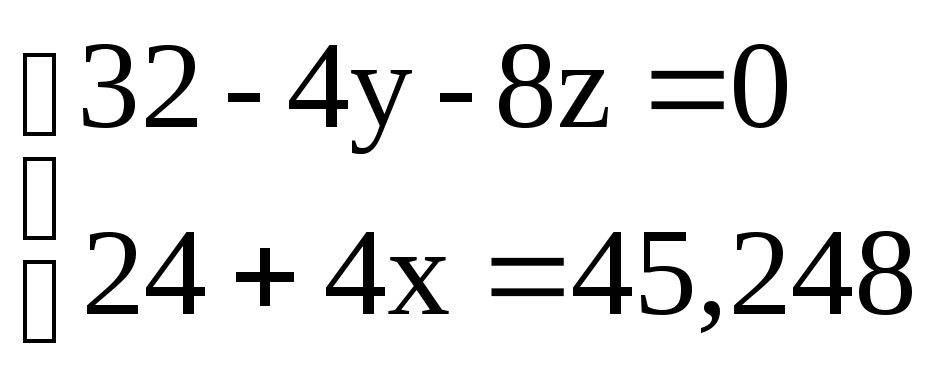
Значения координат точек пересечения центральной осью координатных плоскостей , определенных этими уравнениями, помещены в табл. C6.2

Таблица C6.2

Точки	Координаты, см
	x	y	z
A1	0	–	–
A2	5,312	0	4
A3	5,312	8	0

Центральная ось системы сил показана на рис. C6.1.

3