4. Индексы переменного и постоянного состава и структурных сдвигов.

Индексный метод широко применяется для изучения динамики средних величин и выявления факторов, влияющих на динамику средних. С этой целью исчисляется система взаимосвязанных индексов: переменного, постоянного состава и структурных сдвигов.

Индекс переменного составаI_пер представляет собой отношение двух взвешенных средних величин, характеризующее изменение индексируемого (осредняемого) показателя.

I_пер=

Величина этого индекса характеризует изменение средней взвешенной за счет влияния двух факторов: осредняемого показателя у отдельных единиц совокупности и структуры изучаемой совокупности.

Индекс постоянного (фиксированного) составаI_фикспредставляет собой отношение средних взвешенных с одними и теми же весами (т.е. при постоянной структуре).

I_фикс =

Индекс постоянного состава учитывает изменение только индексируемой величины и показывает средний размер изменения изучаемого показателя у единиц совокупности.

Индекс структурных сдвигов I_стрхарактеризует влияние изменения структуры изучаемого явления на динамику среднего уровня индексируемого показателя.

I_стр=

Под структурными изменениями понимается изменение доли отдельных групп единиц совокупности к общей их численности.

Система взаимосвязанных индексов при анализе динамики средних величин имеет вид:

I_пер=I_фикс*I_стр

5.Примеры решения задач

Пример 1. Имеются данные по предприятию

Изделие	Выпуск продукции, шт. q		Цена единицы продукции, руб. p
	2000г.	2001 г.	2000г.	2001 г.
А	22000	28000	2.0	1.8
Б	7000	12000	6.0	5.0
В	2000	5000	20.0	18.0

Определить:

1) индивидуальные индексы физического объема продукции, цен и товарооборота по каждому изделию;

2) общий индекс товарооборота, агрегатные индексы физического объема и цен;

абсолютные приросты товарооборота за счет изменения объемов производства, цен, за счет совместного действия обоих факторов;

3) показать взаимосвязь показателей.

Решение.

1) Индивидуальные индексы физического объема

i_qA= 28000/22000=121% (рост на 21%)

i_qБ=12000/7000=171% (рост на 71%)

i_qВ=5000/2000=250% (рост в 2,5 раза)

Индивидуальные индексы цен

i_pA=1,8/2=0,9=90% (снижение на 10%)

i_pБ=5/6=0,83=83% (снижение на 17%)

i_pВ=18/20=0,9=90% (снижение на 10%)

Индивидуальные индексы товарооборота

i_{pq А} = (28000*1,8)/(22000*2,0) =114,5% (рост на 14,5%)

i_{pq Б} = (12000*5,0)/(7000*6,0) = 142,9% (рост на 42,9%)

i_{pq В} = (5000*18,0)/(2000*20,0) =225% (рост 2,25%)

2) Изменение по предприятию в целом (по трем изделиям) индивидуальным индексом оценить нельзя, т.к. совокупность неоднородная. Поэтому воспользуемся сводным индексом.

Сводный индекс общего товарооборота

Объем общего товарооборота вырос на 59%. В абсолютном выражении изменение товарооборота составляет:

=200,4-126=74,4 т.р.

Этот рост достигнут за счет изменения двух факторов: изменения уровня цен и изменения количества продукции.

Агрегатный индекс физического объема

Поскольку данный индекс является индексом количественного показателя (объема продукции), вычислим его, применяя базисные веса, т.е. при расчете используем уровень цен базисного периода

Наблюдается рост физического объема продукции на 81%, в абсолютном выражении прирост физического объема продукции равен

=228-126=102т.р.

Агрегатный индекс цен

Поскольку данный индекс является индексом качественного показателя (цен), вычислим его, применяя отчетные веса, т.е. при расчете используем объем производства отчетного периода

Цены снизились на 12%, экономия потребителя за счет изменения цен составила

=200,4-228=-27,6 т.р. (знак «-» указывает на экономию, знак «+» - на перерасход денежных средств потребителя)

3) Взаимосвязь показателей

74,4 =102-27,6 т.р.

Общий вывод: Рост физического объема продукции на 81% обеспечил прирост товарооборота на 102 т.р. Одновременное снижение цен на 12% уменьшило товарооборот на 27,6 т.р. Совместное действие факторов обусловило рост товарооборота на 59%, или 74.4 т.р.

Пример 2. Имеются следующие данные

Изделие	Цена единицы в базисном периоде p0	Выпуск в базисном периоде, шт q0	Изменение физического объема продукции в отчетном периоде по сравнению с базисным
А	110	12000	1,10
Б	16	15000	1,15

Определить индивидуальные и общий индекс физического объема продукции

Решение.

По условию, индивидуальные индексы физического объема продукции по изделиям А и Б составили

i_qA=1.10

i_qБ=1,15

Сводный индекс физического объема продукции I_q определим как среднюю арифметическую из двух индивидуальных индексовi_qA иi_qБ. Исходные данные позволяют рассчитатьI_q по формуле средней арифметической.

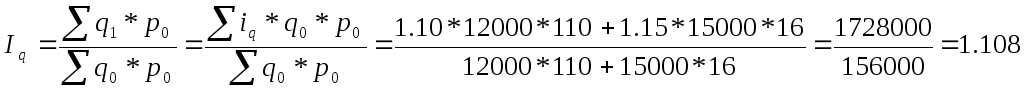, Физический объем выпускаемой продукции вырос на 10,8%

Пример 3. Имеются следующие данные об издержках производства продукции по предприятию

Изделие	Общие издержки производства (тыс. руб.) z*q		Изменение себестоимости единицы продукции в % к базисному периоду
	Базисный период	Отчетный период
А	150,0	174,6	+3
Б	289,0	323,0	-5

Определить среднее изменение себестоимости в отчетном периоде по сравнению с базисным.

Решение.

По условию, индивидуальные индексы себестоимости продукции по изделиям А и Б составили

i_zA=1.03

i_zБ=0.95

Сводный индекс себестоимости I_Z определим как среднюю арифметическую из двух индивидуальных индексов i_zA и i_zБ. Исходные данные позволяют рассчитать I_q по формуле средней гармонической

=97.6%

В среднем по предприятию себестоимость снизилась на 2,4%.

Пример 4. Имеются данные о производстве однородной продукции на двух предприятиях

Предприятие	Выпуск, шт. q		Себестоимость единицы продукции z
	Базисный период	Отчетный период	Базисный период	Отчетный период
№1	18	20	5,0	4,5
№2	22	30	4,6	3,8

Определить изменение средней себестоимости:

1) общее

2) за счет изменения себестоимости единицы продукции

3) за изменения структуры выпуска продукции

4) показать взаимосвязь системы индексов

Решение.

На изменение средних издержек влияют два фактора:

• себестоимость единицы продукции на каждом предприятии

• структура выпуска продукции

Необходимо учитывать как совместное влияние этих факторов, так и их раздельное влияние.

1) совместное влияние факторов на изменение средних издержек производства учитывает индекс переменного состава.

Он представляет собой соотношение двух средних величин, т.е. здесь учитываются и структурные изменения в составе совокупности, и изменение качественного признака у отдельных объектов.

Средняя себестоимость 1 изделия снизилась на 14,6% за счет совместного действия двух факторов

В абсолютном выражении это

=(4,08-4,78)=-70 коп

Т.е. средняя себестоимость 1 изделия снизилась на 70 коп.

2) изменение за счет качественного признака учитывает индекс фиксированного (постоянного) состава

Средняя себестоимость снизилась на 14,3% за счет изменения себестоимости единицы продукции на каждом предприятии

В абсолютном выражении это

=(4,08-4,76)= -68 коп

3) изменение структуры выпуска продукции (т.е. изменение доли предприятий в общем выпуске продукции) учитывает индекс структурных сдвигов.

Средняя себестоимость снизилась на 0,4% за счет изменения структуры выпуска продукции.

В абсолютном выражении это

=(4,76-4,78)=-2коп.

4) Взаимосвязь системы индексов:

I_пер=I_фикс*I_стр.

0,854=0,857*0,996

Взаимосвязь абсолютных изменений:

=+

-70=-68-2

Общий вывод: если бы произошедшие изменения себестоимости продукции не сопровождались структурными изменениями в ее выпуске, то средняя себестоимость снизилась бы на 14,3% (на 68 коп.). Изменение структуры выпуска продукции отдельных предприятий в общем объеме выпуска вызвало снижение себестоимости на 0,4% (2 коп.). Одновременное воздействие обоих факторов снизило среднюю себестоимость продукции на 14,6%, или 70 коп.