
- •Тема 1 сводка и группировка.
- •Понятия статистической сводки и группировки. Виды группировок
- •2. Построение статистических группировок
- •3. Статистические ряды распределения
- •4. Примеры решения задач
- •5. Задачи для самостоятельного решения
- •Тема 2 обобщающие статистические показатели
- •1. Абсолютные показатели
- •2. Относительный показатель планового задания (опп) рассчитывается как отношение уровня, запланированного на предстоящий период, к уровню, фактически сложившемуся в предшествующем периоде.
- •3. Примеры решения задач
- •4. Задачи для самостоятельного решения
- •Тема 3 средние величины
- •1. Степенные средние
- •2. Структурные средние
- •3. Примеры решения задач
- •Задачи для самостоятельного решения.
- •Тема 4 показатели вариации
- •1. Абсолютные и средние показатели вариации.
- •2. Относительные показатели вариации
- •3. Правило сложения дисперсий
- •4. Дисперсия альтернативного признака
- •5. Характеристика закономерности рядов распределения
- •6. Примеры решения задач
- •Тема 5 выборочный метод в экономико-статистических исследованиях
- •Понятие о выборочном исследовании
- •2. Характеристики выборочной совокупности и их распространение на генеральную совокупность.
- •3. Оптимальная численность выборки
- •4. Примеры решения задач
- •5. Задачи для самостоятельного решения
- •Тема 6 статистическое изучение связи
- •1. Основные понятия и предпосылки корреляционно-регрессионного анализа
- •2. Измерение степени тесноты корреляционной связи в случае парной зависимости
- •3. Вычислениепараметров уравнения регрессии
- •4. Примеры решения задач
- •5. Задачи для самостоятельного решения.
- •Тема 7 ряды динамики и их статистический анализ
- •Понятие о статистических рядах динамики
- •2.Показатели динамики социально-экономических явлений.
- •3. Средние показатели в рядах динамики
- •4. Выявление и количественная оценка основной тенденции развития (тренда). Изучение периодических колебаний.
- •4. Примеры решения задач
- •5. Задачи для самостоятельного решения
- •2. Индивидуальные индексы и общие индексы в агрегатной форме
- •3. Общие индексы в преобразованной форме (в форме средних из индивидуальных индексов).
- •4. Индексы переменного и постоянного состава и структурных сдвигов.
- •5.Примеры решения задач
- •6. Задачи для самостоятельного решения.
- •Список рекомендуемой литературы
4. Примеры решения задач
Пример 1.По данным о величине уставного капитала банка рассчитать показатели динамики. Показать взаимосвязь показателей.
-
Год
Уставной капитал, млн. руб.
1998
5,08
1999
5,5
2000
5,9
2001
6,15
Решение.
1) Базисные абсолютные приросты Δубi = yi – уо :
1999 г. 5,5-5,08=0,42 млн.р.
2000 г. 5,9-5,08=0,82 млн.р.
2001 г. 6,15-5,08=1,07 млн.р.
2) Цепные абсолютные приросты Δуцi=yi – yi-1
1999 г. 5,5-5,08=0,42 млн.р.
2000 г. 5,9-5,5 =0,4 млн.р.
2001 г. 6,15-5,9=0,25 млн.р.
3)
Взаимосвязь базисных и цепных абсолютных
приростов
![]() =
∑Δуцi
=
∑Δуцi
1,07=0,42+0,4+0,25 (млн.р.)
4)
Базисные темпы роста
![]()
1999 г. 5,5/5,08=1,083 = 108,3%
2000 г. 5,9/5,08=1,161 = 116,1%
2001 г. 6,15/5,08=1,211=121,1%
5) Цепные
темпы роста ![]()
1999 г. 5,5/5,08=1,083 = 108,3%
2000 г. 5,9/5,5 =1,073 = 107,3%
2001 г. 6,15/5,9=1,042 = 104,2%
6) Взаимосвязь базисных и цепных темпов роста
1,211=1,083*1,073*1,042
7)
Базисные темпы прироста
![]()
1999 г. 0,42/5,08= 0,083 = 8,3 %
2000 г. 0,82/5,08= 0,163 = 16,1%
2001 г. 1,07/5,08= 0,211 = 21,1%
8) Цепные
темпы прироста
![]()
1999 г. 0,42/5,08 = 0,083 = 8,3%
2000 г. 0,4/5,5 = 0,073 = 7,3%
2001 г. 0,25/5,9 = 0,042 = 4,2%
9) Взаимосвязь базисных темпов роста и
прироста
![]() или
или
![]()
|
1999 г. |
8,3%=108,3%-100% |
0,083=1,083-1 |
|
2000 г. |
16,1%=116,1%-100% |
0,161=1,161-1 |
|
2001 г. |
21,1%=121,1%-100% |
0,211=1,211-1 |
10) Взаимосвязь цепных темпов роста и
прироста
![]() или
или
![]()
|
1999 г. |
8,3%=108,3%-100% |
0,083=1,083-1 |
|
2000 г. |
7,3%=107,3%-100% |
0,073=1,073-1 |
|
2001 г. |
4,2%=104,2%-100% |
0,042=1,042-1 |
11)
Средний уровень ряда вычисляется по
формуле
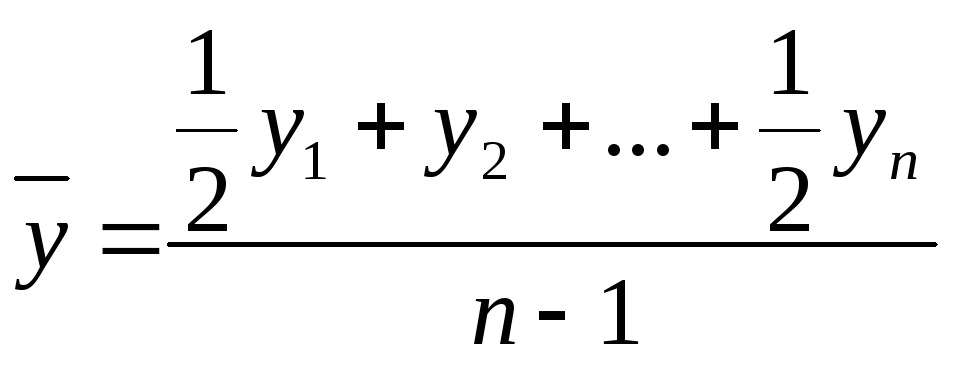 ,
т.к. исходные данные – это моментный
ряд с равноотстоящими датами
,
т.к. исходные данные – это моментный
ряд с равноотстоящими датами
 =
5,67 млн.р.
=
5,67 млн.р.
12) Средний абсолютный прирост
![]() ,
,![]() млн.р.,
млн.р.,
или
![]()
![]() =
0,36 млн.р.
=
0,36 млн.р.
13) Средний темп роста
![]()
![]() =106,6%
=106,6%
или
![]() =106,6%
=106,6%
14)
Средний темп прироста![]() =
=![]() -1,
или
-1,
или
![]() =
=![]() -100%
-100%
![]() =1,066-1=0,066,
=1,066-1=0,066,
или
![]() =
106,6%-100%=6,6%
=
106,6%-100%=6,6%
5. Задачи для самостоятельного решения
Задача 1. По данным о величине уставного капитала банка рассчитать показатели динамики, средние показатели ряда динамики. Показать взаимосвязь показателей.
|
Годы |
1991 |
1992 |
1993 |
1994 |
1995 |
|
Производство тракторов (тыс. шт.) |
45,0 |
47,8 |
50,4 |
55,3 |
58,2 |
Задача 2. По данным, характеризующим численность работающих в организации на первое число каждого месяца определить показатели динамики, средние показатели ряда динамики. Показать взаимосвязь показателей.
|
Дата |
01.01 |
01.02 |
01.03 |
01.04 |
01.05 |
01.06 |
01.07 |
|
Численность работающих |
224 |
229 |
232 |
236 |
229 |
230 |
234 |
Тема 8
ИНДЕКСЫ И ИХ ИСПОЛЬЗОВАНИЕ
В ЭКОНОМИКО-СТАТИСТИЧЕСКИХ ИССЛЕДОВАНИЯХ
1. Понятие, виды, свойства и основные задачи применения
индексов в экономико-статистических исследованиях
Статистический индекс – это относительная величина сравнения сложных совокупностей и отдельных их единиц. При этом под сложной понимается такая статистическая совокупность, отдельные элементы которой по отдельности не подлежат суммированию.
Основным элементом индексного отношения является индексируемая величина, под которой понимается значение признака статистической совокупности, изменение которой является объектом изучения. Так, при изучении изменения цен индексируемой величиной является цена единицы товарар; при изучении изменения физического объема товарной массы – данные о количестве товаров в натуральных измерителяхq.
Способы построения индексов зависят от содержания изучаемых показателей, методологии расчета исходных статистических показателей, имеющихся в распоряжении исследователя статистических данных и целей исследования.
По степени охвата элементов совокупности различают индивидуальные и сводные (общие) индексы. Индивидуальные индексы (обозначаются буквойi) характеризуют изменение только одного элемента совокупности.Сводный (общий) индекс (обозначаетсяI) отражает изменение по всей совокупности элементов сложного явления.
В зависимости от содержания и характера индексируемой величины различают индексы количественных (объемных) показателей (например, индекс физического объема продукции) и индексыкачественныхпоказателей (например, индексы цен, себестоимости).
В зависимости от методологии расчета различают агрегатныеиндексы исредние из индивидуальных индексов (илипреобразованную форму индексов). Последние в свою очередь делятся на средние арифметические и средние гармонические.
Если сравнивают друг с другом не два момента (периода) времени, а более, то выделяют цепнуюибазиснуюсистему индексов.
Индексы обладают синтетическими и аналитическими свойствами. Синтетические свойства состоят в том, что посредством индексного метода производится соединение (агрегирование) в целое разнородные единиц статистической совокупности. Аналитические свойства состоят в том, что посредством индексного метода определяется влияние факторов на изменение изучаемого показателя. Таким образом, с помощью индексных показателей решаются следующие основные задачи:
1) характеристика общего изменения сложного экономического показателя или формирующих его отдельных показателей-факторов;
2) выделение в изменении сложного показателя влияния одного из факторов путем элиминирования влияния других факторов.
Формулы для расчета индексов приведены далее на примере индексируемых цен (p), физического объема продукции (q), товарооборота (pq), изменяющихся во времени.
