Контрольная работа / Решение 12038 задача 1-5

Задание 1.

Найти все комплексные значения следующих выражений и изобразить их на комплексной плоскости.

а)

б)

Решение:

а) Воспользуемся соотношением: .

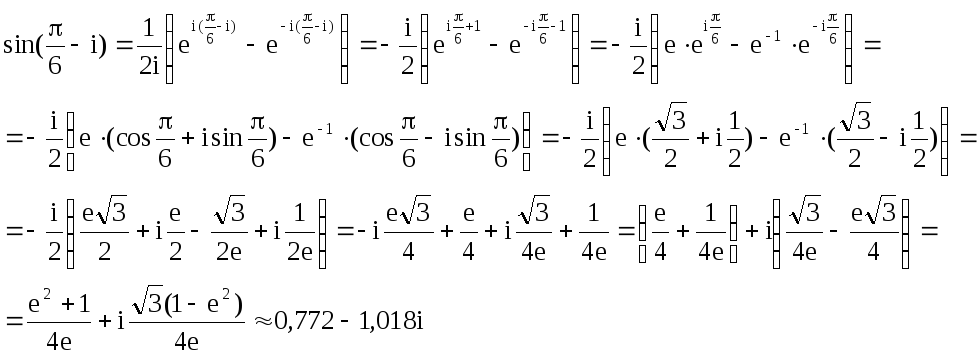
Изобразим точку (0,772; -1,018) на комплексной плоскости:

б) Представим число в тригонометрическом виде: , где

Согласно формулы Муавра:

.

В нашем случае n = ½. Тогда:

k = 0:

k = 1:

Ответ: чертежи выше.

Задание 5.

Вычислить интеграл по замкнутому контуру С с помощью вычетов.

;

Решение:

Найдем особые точки подинтегральной функции – нули знаменателя.

Для этого решим уравнение:

Вычислим для полученных особых точек и проверим принадлежность их кругу :

: > 1,5 – не принадлежит кругу.

: > 1,5 – не принадлежит кругу.

: < 1,5 – принадлежит кругу.

Точка - простой полюс функции  , т.к. она является простым нулем знаменателя.

Вычислим вычет в простом полюсе функции :

Запишем знаменатель в показательной форме:

, где

Получим выражение:

Тогда

Ответ: